基于SOA海鸥优化算法的三维曲面最高点搜索matlab仿真

news2024/10/7 10:25:09

1.程序功能描述

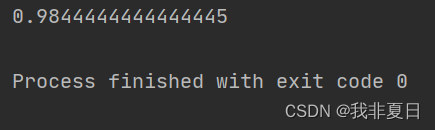
2.测试软件版本以及运行结果展示

3.核心程序

4.本算法原理

5.完整程序

1.程序功能描述

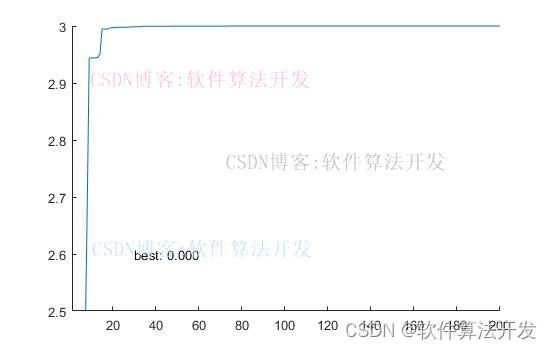
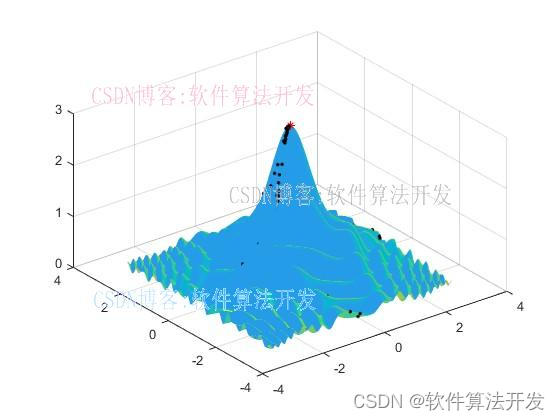
基于SOA海鸥优化算法的三维曲面最高点搜索matlab仿真，输出收敛曲线以及三维曲面最高点搜索结果。

2.测试软件版本以及运行结果展示

MATLAB2022A版本运行

3.核心程序

...................................................................
for ij = 1:Mgen
    
    % 初始化本代最佳适应度及对应解
    yfit  = 0.0;
    xbest = zeros(1,2); % 初始设定为零向量
    idx0  = 0;
    
    % 计算当前种群中每个个体的适应度
    for i = 1:Npop
        tmp = Xpop(i,:);
        x = func_Decode(tmp, Nvar);
        Dec_Pop(i,:) = x; % 解码并存储
        fitness(i) = func_Evaluate(x); % 计算适应度
        
        % 更新最佳解
        if fitness(i) > yfit
           yfit  = fitness(i);
           idx0  = i;
           xBest = x;
        end
    end
    
    % 复制当前种群用于下一步操作
    Xpop_tmp = Xpop;
    
    % 执行交叉操作
    for i = 1:2:Npop
        i1 = func_Tournament(fitness,Prob0);
        i2 = func_Tournament(fitness,Prob0);
        tmp1 = Xpop(i1,:);
        tmp2 = Xpop(i2,:);
        r = rand;
        if (r < Prob1)
            Xpair = func_cross(tmp1,tmp2);
            Xpop_tmp(i,:) = Xpair(1,:);
            Xpop_tmp(i+1,:) = Xpair(2,:);
        else
            Xpop_tmp(i,:) = tmp1;
            Xpop_tmp(i+1,:) = tmp2;
        end
    end
    
    % 执行变异操作
    for i = 1:Npop
        Xpop0 = Xpop_tmp(i,:);
        Xpop1 = func_Mut(Xpop0,Prob2);
        Xpop_tmp(i,:) = Xpop1;
    end
    
    % 保留当前代最佳个体
    Xpop_tmp(1,:) = Xpop(idx0,:);
    Xpop = Xpop_tmp;
end
58

4.本算法原理

海鸥优化算法(SOA Seagull Optimization Algorithm)是一种新兴的启发式优化方法，它借鉴自然界中海鸥在觅食时展现出的智能行为，如集群协作、竞争与探索策略，来解决复杂的优化问题，尤其是三维曲面的最高点搜索问题。该算法通过模拟海鸥群体在空中飞行、搜寻食物源的过程，探索解空间以找到全局最优解。

海鸥优化算法的核心在于模拟海鸥的三种基本行为：搜索飞行、跟随飞行和掠食飞行。这些行为被转化为算法中的探索、开发和优化策略，旨在高效地搜索解空间。