**
Heatmap 方法汇总
高斯热图与坐标回归方法探讨
L1与 L2 Loss的对比分析
关键点之热力图Heatmap与坐标FC回归
Heatmap-based和Regression-based
一般来说,我们可以把姿态估计任务分成两个流派:Heatmap-based和Regression-based。
其主要区别在于监督信息的不同,Heatmap-based方法监督模型学习的是高斯概率分布图,即把GroundTruth中每个点渲染成一张高斯热图,最后网络输出为K张特征图对应K个关键点,然后通过argmax或soft-argmax来获取最大值点作为估计结果。这种方法由于需要渲染高斯热图,且由于热图中的最值点直接对应了结果,不可避免地需要维持一个相对高分辨率的热图(常见的是64x64,再小的话误差下界过大会造成严重的精度损失),因此也就自然而然导致了很大的计算量和内存开销。
Regression-based方法则非常简单粗暴,直接监督模型学习坐标值,计算坐标值的L1或L2 loss。由于不需要渲染高斯热图,也不需要维持高分辨率,网络输出的特征图可以很小(比如14x14甚至7x7),拿Resnet-50来举例的话,FLOPs是Heatmap-based方法的两万分之一,这对于计算力较弱的设备(比如手机)是相当友好的,在实际的项目中,也更多地是采用这种方法。
说到Regression-based方法的优点,那是就是好呀就是好,可以简单总结为以下三点:
1、没有高分辨率热图,无负一身轻。计算成本和内存开销一起大幅降低。
2、输出为连续的,不用担心量化误差。(Heatmap-based输出的热图最大值点在哪,对应到原图的点也就确定了,输出热图的分辨率越小,这个点放大后对应回去就越不准。Regression-based输出为一个数值,小数点后可以有很多位,精度不受缩放影响)
3、可拓展性高。不论是one-stage还是two-stage,image-based还是video-based,2D还是3D,Regression-based方法都可以一把梭。此前就有用这种方法来将2D和3D数据放在一起联合训练的文章。这是Heatmap-based方法做不到的,因为输出是高度定制化的,2D输出必须渲染2D高斯热图,3D就必须渲染3D的高斯热图,计算量和内存开销也蹭蹭蹭地暴涨。
而Heatmap-based方法通过显式地渲染高斯热图,让模型学习输出的目标分布,也可以看成模型单纯地在学习一种滤波方式,将输入图片滤波成为最终希望得到的高斯热图即可,这极大地简化了模型的学习难度,且非常契合卷积网络的特性(卷积本身就可以看成一种滤波),并且这种方式规定了学习的分布,相对于除了结果以外内部一切都是黑盒的Regression-based方法,对于各种情况(遮挡、动态模糊、截断等)要鲁棒得多。
基于以上种种优点,Heatmap-based方法在姿态估计领域是处于主导地位的,SOTA方案也都是基于此,这也导致了一种学术研究与算法落地的割裂,你在各种数据集和比赛里指标刷得飞起,但项目落地时我们工程师却只能干着急,因为你用的方法又慢又吃内存,真实项目里根本没法用啊。
终于,这一天有篇文章站出来说,重铸Regression荣光,吾辈义不容辞!不仅将Regression-based方法提到了超越Heatmap-based方法的高度,还保留了其一直以来的节省计算资源和内存资源的优点,真正做到了又快又准,简直是项目落地算法工程师的福音,接下来就让我们一起来学习一下这篇文章。
Human Pose Regression with Residual Log-likelihood Estimation(ICCV 2021 Oral)
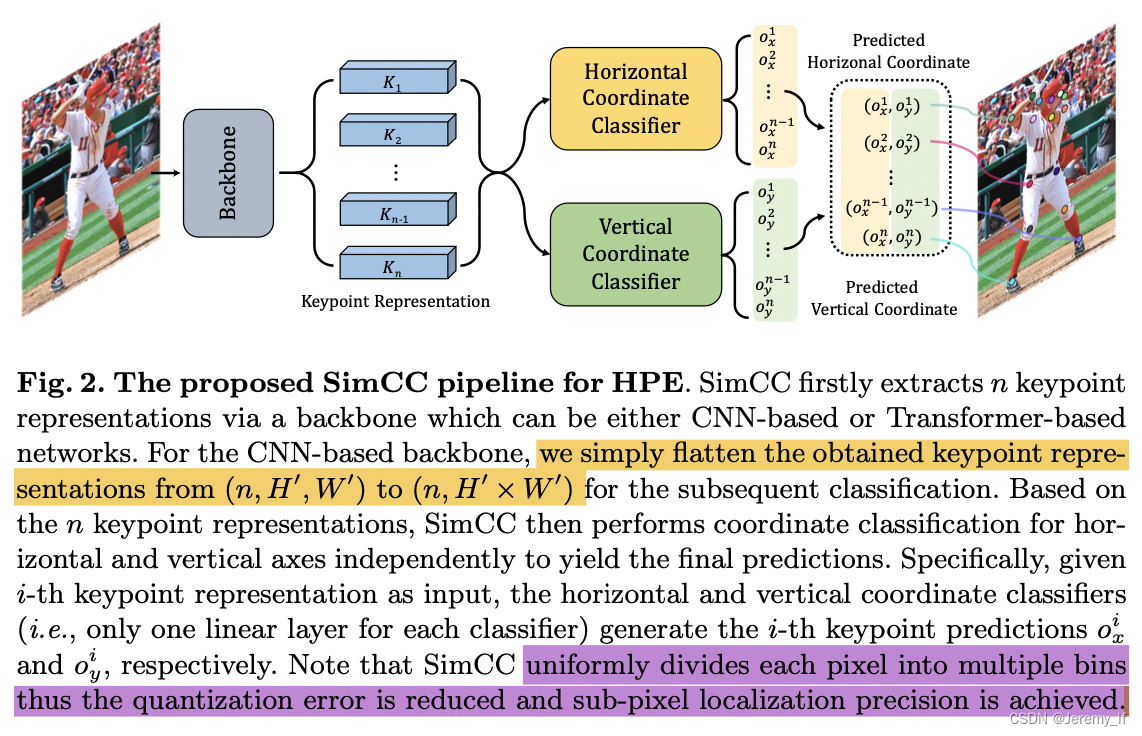
SimCC: a Simple Coordinate Classification Perspective for Human Pose Estimation
code|https://github.com/leeyegy/SimCC/blob/main/lib/dataset/JointsDataset.py
论文解读
论文解读2
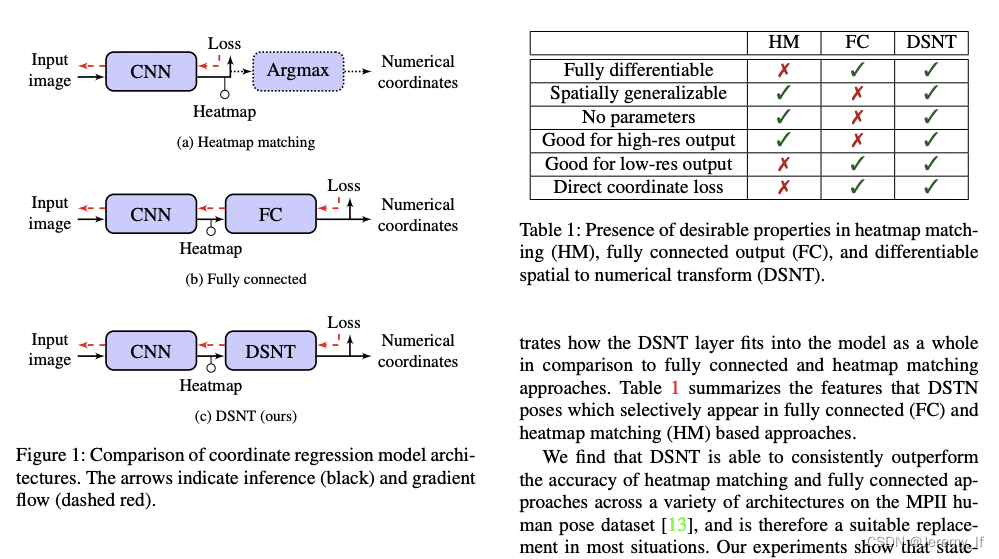
Numerical Coordinate Regression with Convolutional Neural Networks(DSNT)
论文解读
代码链接
本文提出一种新的处理方法,称为differentiable spatial to numerical transform(DSTN),通过DSNT处理(没添加额外参数),直接对坐标进行监督。DSNT是对heatmap进行处理的,思路如下图所示。最后的处理过程,就是将heatmap通过softmax,得到一个基于heatmap的概率分布,再通过这个概率分布,与预设好的X,Y(坐标轴)进行点乘,得到坐标的期望值。监督损失也是建立在这个期望值上的。
目前主流的关键点回归就两种做法:
(1) 采用全连接层直接回归坐标点,例如yolo-v1。该类做法的优点是输出即为坐标点,训练和前向速度可以很快,且是端到端的全微分训练;缺点是缺乏空间泛化能力,也就是说丢失了特征图上面的空间信息。
空间泛化是指模型训练期间在一个位置获得的知识在推理阶段推广到另一个位置的能力 ,举例来说,如果我在训练阶段有一个球一直在图片左上角,但是测试阶段球放在了右下角了,如果网络能够检测或者识别出来,那么就说该模型具备空间泛化能力。可以看出坐标点回归任务是非常需要这种能力的,因为我不可能每一个位置的图片都训练到。全卷积模型具备这种能力的原因是权重共享,然而对于全连接层,在2014年的Network in network论文指出fully connected layers are prone to overfitting, thus hampering the generalization ability of the overall network。也就是说如果采用全连接输出坐标点方式是会极大损害空间泛化能力的,其实从理论上也很容易分析出来:在训练阶段有一个球一直在图片左上角,reshape拉成一维向量后,全连接层的激活权重全部在上半部分,而下半部分的权重是没有得到训练的,当你测试时候输入一张球放在了右下角图片,拉成一维向量后,由于下半部分权重失效,理论上是预测不出来的,即没有空间泛化能力。而卷积操作由于权重共享,是可以有效避免的。总结一下:全连接方式所得权重严重依赖于训练数据的分布,非常容易造成过拟合。
(2) 采用预测高斯热图方式,然后argmax找出峰值对应的索引即为坐标点,例如cornernet、grid-rcnn和cpn等等。以单人姿态估计为例,输出是一张仅仅包含一个人的图片,输入是所有关键点的高斯热图,label是基于每个关键点生成的高斯图。如果每个人要回归17个关键点,那么预测输出特征图是(batch,h_o,w_o,17),即每个通道都是预测一个关节点的热图,然后对每个通道进行argmax即可得到整数型坐标。
基于高斯热图输出的方式会比直接回归坐标点精度更高,原因并不是高斯热图输出方式的表达好,而是由于其输出特征图较大,空间泛化能力较强导致的,那么自然能解释如果我依然采用(1)直接回归坐标的方法预测,但是我不再采用全连接,而是全卷积的方式依然会出现精度低于高斯热图的现象,原因是即使全卷积输出,但是像yolo-v2、ssd等其输出特征图很小,导致空间泛化能力不如方法(2)。
单从数值上来看,肯定是直接回归坐标点方式好啊,因为直接回归坐标点的话,输出是浮点数,不会丢失精度,而高斯热输出肯定是整数,这就涉及到一个理论误差下界问题了。假设输入图片是512x512,输出是缩小4倍即128x128,那么假设一个关键点位置是507x507,那么缩小4倍后,即使没有任何误差的高斯热图还原,也会存在最大507-126*4=3个像素误差,这个3就是理论误差下界。如果缩小倍数加大,那么理论误差下界还会上升。所以目前大部分做法折中考虑速度和精度,采用缩小4倍的方式。
该类做法优点是精度通常高于全连接层直接回归坐标点方法;缺点也很明显,从输入到坐标点输出不是一个全微分的模型,因为从heatmap到坐标点,是通过argmax方式离线得到的(其实既然argmax不可导,那就用soft argmax代替嘛,有论文确实是这么做的)。并且由于其要求的输出特征图很大,训练和前向速度很慢,且内存消耗大。
在heatmap产生坐标的过程中,缺点:(1)使用的argmax之类的处理过程,是不可微分的,不能进行直接学习;(2)heatmap到坐标的过程中,存在着量化误差。heatmap与输入分辨率的下采样倍数越大,量化误差越大。更值得注意的是,监督是建立于heatmap 上的,这将导致损失函数与我们的度量(坐标上)之间相隔开来了。在推理时,我们只使用其中的某个(某几个)像素进行数值坐标计算,但在训练时,对所有像素都会造成损失。
总结一下,虽然高斯热图预测的精度通常高于回归的方法,但是其存在几个非常麻烦的问题:(1) 输出图很大,导致内存占用多、推理和训练速度慢;(2) 存在理论误差下界;(3) mse loss可能会导致学习出来的结果出现偏移;(4) 不是全微分模型;
Hourglass:Stacked Hourglass Networks for Human Pose Estimation
Bottom-Up Human Pose Estimation Via Disentangled Keypoint Regression
Towards accurate multi-person pose estimation in the wild
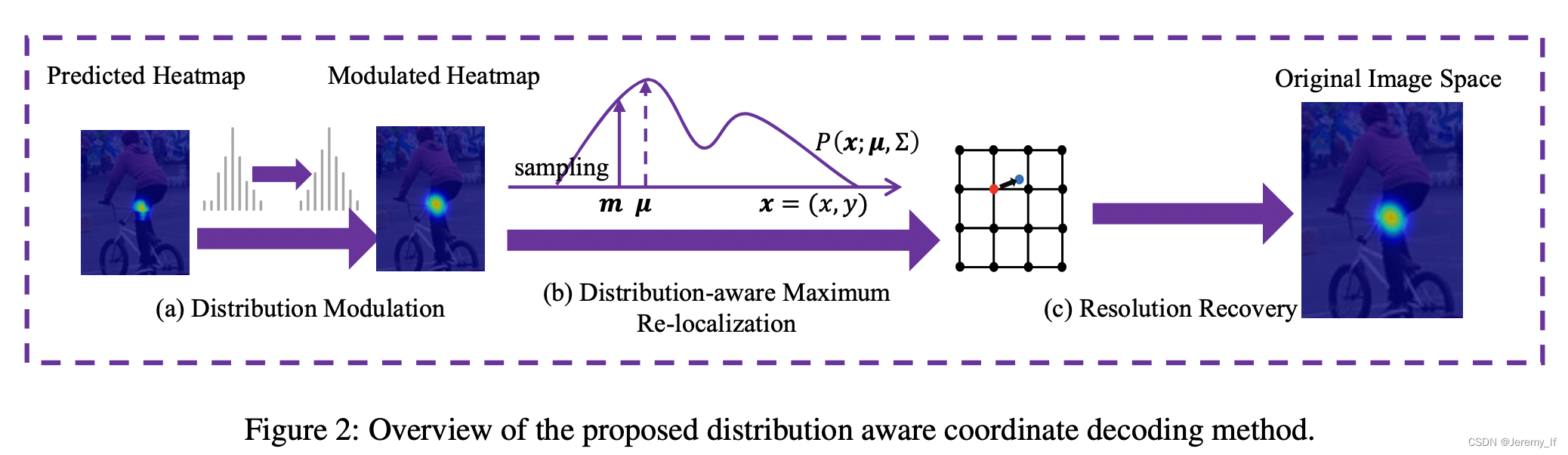
Distribution-Aware Coordinate Representation for Human Pose Estimation
DARK
参考文章2
后处理实现