算法意义

C
→
Y
→
V
→
e
C\rightarrow Y \rightarrow V \rightarrow e
C→Y→V→e
符号
| 符号 | 含义 | – |
|---|---|---|
| Ω \Omega Ω | 研究图像区域 | |
| ∂ Ω \partial\Omega ∂Ω | 研究图像区域的边界 | |
| ϕ ( x , y ) \phi(x,y) ϕ(x,y) | 代求电导率 | |
| σ ( x , y ) \sigma(x,y) σ(x,y) | 节点电压 e 电导率 | |
| j n ( x , y ) j_n(x,y) jn(x,y) | 注入表面电流密度分布 | |
| N | 同态分割网格的个数 | |
| Δ x \Delta x Δx | x轴向的网格边长 | |
| Δ y \Delta y Δy | y轴向的网格边长,令 p i = Δ x Δ y p_i=\Delta x\Delta y pi=ΔxΔy | |
| C ={ c x , y c_{x,y} cx,y} | 连续电导率分布在实数中离散化, c x , y c_{x,y} cx,y |
在该方法中,离散化域被建模为导纳网络,其中基尔霍夫电流 压定律的应用为每个单元产生以下线性方程:
| 符号 | 含义 | – |
|---|---|---|
| V x , y V_{x,y} Vx,y | (x,y)节点处的离散电势 | |
| Y y + Y_{y^+} Yy+ | 导纳项 |
- 电压 = 电压/导纳率
V x , y = 1 Y x − + Y x + + Y y − + Y y + ( Y x + V x + Δ x , y + Y x − V x − Δ x , y + Y y + V x , y + Δ y + Y y − V x , y − Δ y − I i e ) (1) V_{x,y}=\frac{1}{Y_{x^{-}}+ Y_{x^{+}}+ Y_{y^{-}}+ Y_{y^{+}} }( Y_{x^{+}}V_{x+\Delta x,y}+ Y_{x^{-}}V_{x-\Delta x,y}+ Y_{y^{+}}V_{x,y+\Delta y}+ Y_{y^{-}}V_{x,y-\Delta y} - I_{ie}) \tag{1} Vx,y=Yx−+Yx++Yy−+Yy+1(Yx+Vx+Δx,y+Yx−Vx−Δx,y+Yy+Vx,y+Δy+Yy−Vx,y−Δy−Iie)(1)
| 符号 | 含义 | – |
|---|---|---|
| V x , y V_{x,y} Vx,y | (x,y)节点处的离散电势 | |
| I i e I_{ie} Iie | 方程的已知电源项(源) |
导纳项计算如下(由C推断Y(C是连续的初始假设的,Y是离散的),以
Y
y
+
Y_{y^+}
Yy+为例):
Y
y
+
=
c
x
+
∗
Δ
y
Δ
x
=
2
c
x
,
y
c
x
+
Δ
x
,
y
c
x
,
y
+
c
x
+
Δ
x
,
y
∗
Δ
y
Δ
x
(2)
Y_{y^+}=c_{x^+}*\frac{\Delta y}{\Delta x}=\frac{2c_{x,y} c_{x+\Delta x,y} }{c_{x,y}+ c_{x+\Delta x,y}} *\frac{\Delta y}{\Delta x} \tag{2}
Yy+=cx+∗ΔxΔy=cx,y+cx+Δx,y2cx,ycx+Δx,y∗ΔxΔy(2)
为了在N个未知数中求解N个方程的平方线性系统,可以使用迭代或直接方法。
Iterative solution
- 令
V
n
+
1
V^{n+1}
Vn+1表示第n+1次
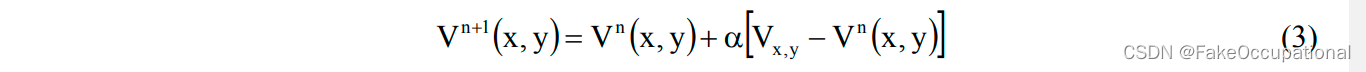
过松弛参数1 < α \alpha α< 2, V ( x , y ) V(x,y) V(x,y)的计算使用公式1.
Non-iterative solution(线性系统)
Y ( N − 1 , n − 1 ) ∗ V ( N − 1 , 1 ) = I ( N − 1 , 1 ) (4) Y_{(N-1,n-1)}*V_{(N-1,1)} =I_{(N-1,1)}\tag{4} Y(N−1,n−1)∗V(N−1,1)=I(N−1,1)(4)
| 符号 | 含义 | – |
|---|---|---|
| V = [ V 1 … V N − 1 ] T V=[V_1… V_{N-1} ]^T V=[V1…VN−1]T | 未知离散电压分布 | |
| I = [ I 1 … I N − 1 ] I=[I_1… I_{N-1} ] I=[I1…IN−1] | 已知离散电流分布 | |
| Y = [ y i j ] i = 1 … N − 1 j = 1 … N − 1 Y=[y_{ij}]_{i=1…N-1}^{j=1…N-1} Y=[yij]i=1…N−1j=1…N−1 | 电导率矩阵 |
,其中每行都有所有零元素,但通常有五个元素除外,如等式(1)所示
通过求Y逆,可以获得线性系统的解向量V
Computed voltages
为了收集计算的电压,通过放置在身体表面上的电极施加多个P电流注入。
所有实现的重构算法都需要为每个注入模式计算定义良好的电极对之间的电压差的数量G。
所计算的电压被存储到M = P*G个向量 g c o m p g^{comp} gcomp中,并且可以通过求解系统(4)的P倍并考虑V向量的对应元素之间的差异来评估它们:
g c o m p ( c ) = T V ′ = T Y ′ − 1 I ′ (5) g^{comp}(c)= TV'=TY'^{-1}I' \tag 5 gcomp(c)=TV′=TY′−1I′(5)
其中列向量c是通过堆叠先前引入的c矩阵的行而获得的,其通用元素ci表示第i个像素的电导率;T是一个变换矩阵,它只从与电极相关的单元中提取电压,并且其行具有除两个值为1和-1之外的所有零元素;

是两个向量,其中Vj是
I
=
I
j
I=I_j
I=Ij时的系统(4)的解;Y’是块对角矩阵
其中每个块仅由Y给出。因此,
g
c
o
m
p
(
c
)
g^{comp}(c)
gcomp(c)的元素
g
i
j
g_{ij}
gij是第i个和第j个电极之间存在的电压差。
Measured voltages
为了收集测量的电压,模拟中使用的相同电流注入模式应通过放置在必须估计电导率的真实物体表面上的电极施加。在这项工作中,通过使用导纳法对所考虑的电导率分布(见图1)进行模拟,获得了测量电压,并将其存储在 M × 1 M×1 M×1的向量 g m e a s g^{meas} gmeas。
3. The Newton-Raphson reconstruction algorithm
目前,EIT中使用重建算法来解决逆问题,即通过find表面电压和电流密度来找到电导率分布
Newton-Raphson(N&R)方法的目的是最小化误差函数e, 其中e是从实际电导率分布测量的电压差和从给定的已知离散电导率分布计算的电压差之间的矢量。定义如下:
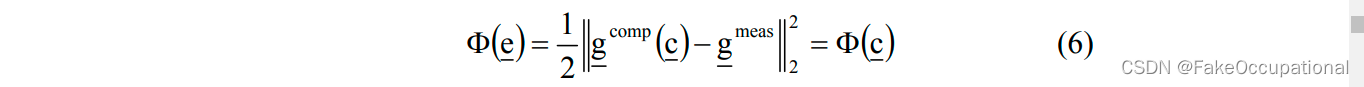
- c = c 1 c =c ^1 c=c1初始化,向前传播 ,并计算 g c o m p ( c 1 ) g^{comp}(c ^1) gcomp(c1)
- 计算 e 1 e^1 e1
- c 1 + Δ c 1 = c 2 c^1 + \Delta c^1 = c^2 c1+Δc1=c2
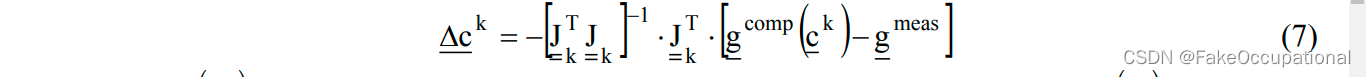
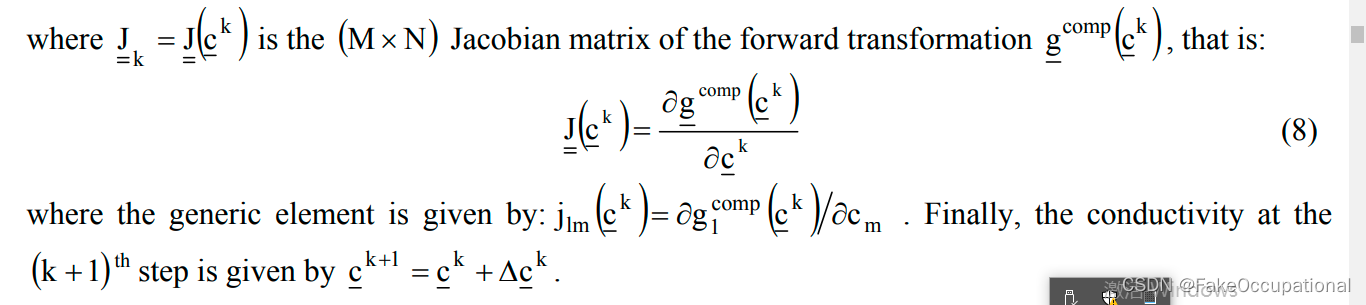
- 迭代至收敛
CG
人体区域电阻抗层析成像算法研究
A Lagrange-Newton Method for EIT/UT Dual-Modality Image Reconstruction †
人体区域电阻抗层析成像系统硬件设计
https://koreascience.kr/article/CFKO200333239336420.pdf