1、二元线性丢番图方程

方程ax +by = c被称为二元线性丢番图方程，其中a、b、c是已知整数，x、y是变量,问是否有整数解。
ax + by= c实际上是二维x-y平面上的一条直线，这条直线上如果有整数坐标点，方程就有解，如果没有整数坐标点，就无解。

如果存在一个解，就有无穷多个解。

1.1有解的判断条件和通解的形式

定理：设a，b是整数且gcd(a, b)=d。如果d不能整除c，那么方程ax + by=c没有整数解，如果d能整除c，那么存在无穷多个整数解。

解释：令a=da'，b= db'；有ax+by = d(a' x +b'y)=c；如果x、y、a'、b'都是整数，那么c必须是d =gcd(a, b)的倍数，才有整数解。

如果 $(x_0,y_0)$ 是方程的一个特解，所有的解（通解）可的形式：x= $x_0$ +(b/d)n，y= $y_0$ - (a/d)n，其中n是任意整数。

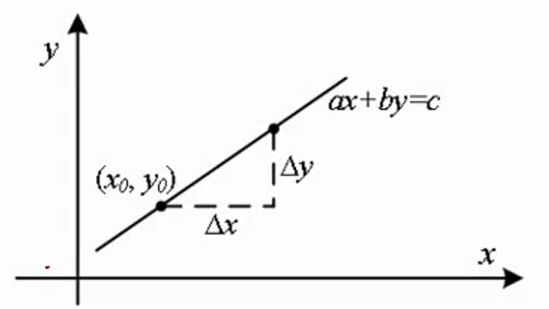
说明: x值按b/d递增，y值按- a/d递增。设 $(x_0,y_0)$ 是一个格点（格点是指x、y坐标均为整数的点),移动到直线上另一个点 $(x_0+\Delta x,y_0+\Delta y)$ ，有 $a\Delta x+b\Delta y=0$ 。△x和Ay必须是整数， $(x_0+\Delta x,y_0+\Delta y)$ 才是另一个格点。

$\Delta x$ 最小是多少?因为a/d与b/d互素，只有 $\Delta x$ = b/d， $\Delta y$ =- a/d时， $\Delta x$ 和 $\Delta y$ 才是整数，并满足a $\Delta x$ +b $\Delta y$ = 0。

定理概况为: ax + by= c有解的充分必要条件是d = gcd(a, b)能整除c。

例:
(1）方程18x + 3y = 7没有整数解，因为gcd(18，3) = 3，3不能整除7;

(2）方程25x + 15y = 70存在无穷个解，因为gcd(25,15)= 5且5整除70，一个特解是 $x_0$ =4， $y_0$ = -2，通解是x=4 + 3n，y = -2- 5n

1.2例题一：线段上的格点数量

【题目描述】在二维平面上，给定两个格点 $p_1=(x_1,y_1)$ 和 $p_2=(x_2,y_2)$ ，问线段 $p_1p_2$ 上除了 $p_1,p_2$ 外还有几个格点?设 $x_1< x_2$ 。

【思路】
首先利用 $p_1,p_2$ 把线段表示为方程ax + by = c的形式，它肯定有整数解。
然后在线段范围内，根据x的通解的表达式 $x = x_0+ (b/d)n$ ，当 $x_1<x<x_2$ 时，求出n的取值情况有多少个，这就是线段内的格点数量。

计算步骤:

(1)、用 $p_1(x_1,y_1)$ 、 $p_2(x_2,y_2)$ 表示线段，线段表示为:

$(y_2-y_1)x + (x_1-x_2)y = y_2x_1-y_1x_2$

(2)、对照ax + by = c，得:
$a = y_2-y_1, b = x1_-x_2,c = y_2x_1-y_1x_2$

$d = gcd(a,b) = gcd(\left | y_2-y_1 \right |,\left |x1-x2 \right |)$

(3)、对照通解公式 $x = x_0+ (b/d)n$ n，令特解是x，代入限制条件 $x_1<x<x_2$ ，有:
$x_1< x+((x_1-x_2)/d)n < x2$

当-d < n< 0时满足上面的表达式，此时n有d-1种取值，即线段内有d-1个格点。

2、方程的特解与扩展欧几里得算法

求解方程ax + by = c的关键是找到一个特解。
根据定理的描述，解和求GCD有关;
求特解用到了欧几里得求GCD的思路，称为扩展欧几里得算法。

2.1扩展欧几里得算法

方程ax + by = gcd(a, b)，根据定理，它有整数解
定理：设a, b是整数且gcd(a, b)=d。如果d不能整除c，那么方程ax + by=c没有整数解，如果d能整除c，那么存在无穷多个整数解。
扩展欧几里得算法求一个特解 $(x_0,y_0)$ 的代码:

def exgcd(a,b):
    if b == 0:return 1, 0
    x,y = exgcd(b,a % b)
    return y, x - a // b * y    # 返回特解xo,yo
a,b = map (int,input ().split())#   试试6x+15y=3
x,y = exgcd (a,b)#计算得到特解
print(x, y)

2.2扩展欧几里得算法与方程ax+by=c的特解

用扩展欧几里得算法得到ax +by =ged(a,b)的一个特解后，再利用它求方程ax +by= c的一个特解。步骤如下:
(1）判断方程ax +by = c是否有整数解，即gcd(a,b)能整除c。记d= gcd(a,b)。
(2）用扩展欧几里得算法求ax + by = d的一个特解 $x_0,y_0$
(3）在 $ax_0 + by_0= d$ 两边同时乘以c/d，得： $ax_0c/d + by_0c/d=c$ （目的是构造c，这样和ax + by= d就能消掉c）