线段树的原理和应用

news2025/1/18 8:56:08

目录

一、前言

二、线段树的概念

1、区间最值问题RMQ (Range Minimum/Maximum Query)

（1）暴力法

（2）高效的办法：线段树

（3）把数列放在二叉树上

（4）查询最小值的复杂度

2、线段树的构造

3、线段树的树结构

三、例题应用

1、最大数（lanqiaoOJ题号826）

（1）初始建一棵空树 build(p, pl, pr)

（2）更新线段树 update()

（3）查询

2、选数异或（2022年省赛，lanqiaoOJ题号2081）

（1）暴力（%40）

（2）动态规划+字典（100%）

（3）线段树（100%）

一、前言

本文讲了线段树的概念和两道例题，建议自己要再多看几眼代码进行思考，第一遍其实我还没有理解透彻为什么要这么做，多看代码多思考。

二、线段树的概念

  • 考核最多的高级数据结构
  • 从初级水平到中级水平的标志：在掌握线段树之后才能说 “我真正进入了算法竞赛的大门。”
  • 应用背景：区间修改、区间查询、区间合并。

1、区间最值问题RMQ (Range Minimum/Maximum Query)

长度为 n 的数列 {a1, a2, ..., an}

（1）求最值：给定 i,j<=n，求 {ai, ...,aj} 区间内的最值。

（2）修改元素：给定 k 和 x，把 a 改成 x。

（1）暴力法

用普通数组存储数列：

查询最值：区间内的最值，复杂度 O(n)

修改元素：复杂度 O(1)

暴力法复杂度：如果有 m 次 “修改元素+查询最值”，总复杂度 O(mn)。

m,n>10^5，O(mn)>10^10

（2）高效的办法：线段树

  • 用线段树，对 n 个数进行 m 次 “修改元素+查询最值”，复杂度：O(mlogn)
  • 线段树：一种用于区间处理的数据结构。
  • 基于二叉树。

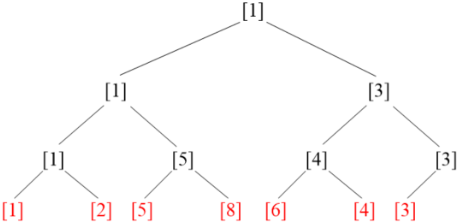
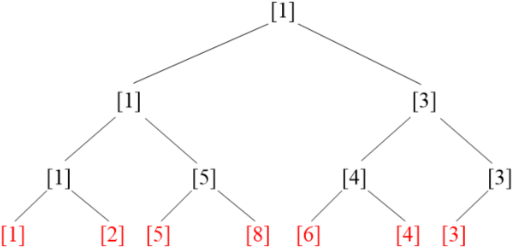
（3）把数列放在二叉树上

例：查询 {1, 2, 5, 8, 6, 4, 3} 的最小值

首先，把数放在二叉树上：

每个结点上的数字是这个结点的子树的最小值。

（4）查询最小值的复杂度

查询某个区间的最小值，只需要 O(logn) 次。

思考：如何在二叉树上定位某个区间?

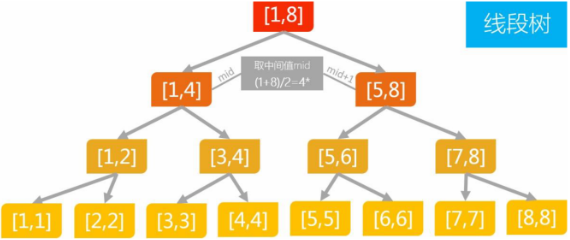
2、线段树的构造

  • 线段树是建立在线段（或者区间）基础上的树，树的每个结点代表一条线段 (或者称为区间) [L, R]。
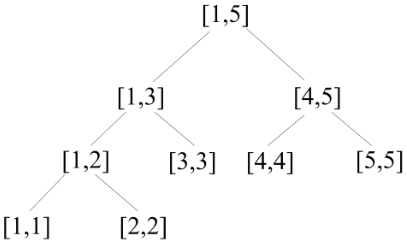
  • 例：线段 [1, 5] 的线段树。

线段 [L,R]：L是左子结点，R是右子结点。

（1）L = R。它是一个叶子结点。

（2）L < R。有两个儿子，左儿子代表区间 [L,M]，右儿子代表区间 [M+1,R]，其中 M = (L + R) / 2。

【线段树的复杂度】

  • 每步处理，从二叉树的根结点开始到最下一层，最多需要更新 log4n 个结点，复杂度 O(logn)；
  • 一共有 n 个数字需要处理，总复杂度 O(nlogn)。
  • 线段树把 n 个数按二叉树进行分组，每次更新有关的结点时，这个结点下面的所有子结点都隐含被更新了，从而大大地减少了处理次数。

【区间查询】

  • 区间查询问题 (最值、区间和) 是线段树的一个基本应用场景。
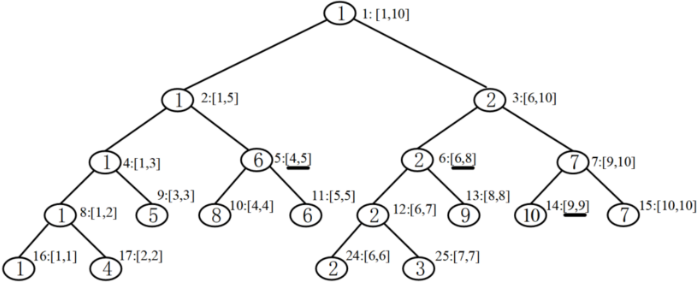
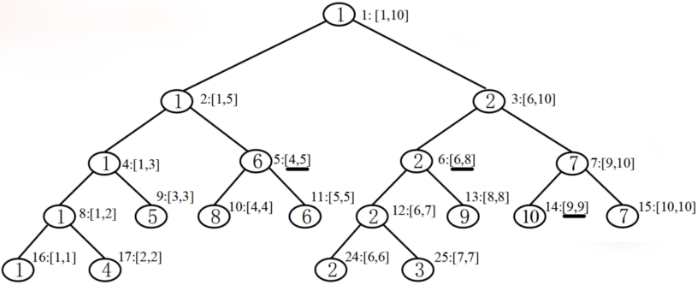
  • 以数列 {1, 4, 5, 8, 6, 2, 3, 9, 10, 7} 为例。
  • 首先建立一棵用完全二叉树实现的线段树，用于查询任意子区间的最小值。
  • 每个结点上圆圈内的数字是这棵子树的最小值。
  • 圆圈旁边的数字，例如根结点的 "1:[1,10]"，1 表示结点的编号，[1,10] 是这个结点代表的元素范围，即第 1 到第 10 个元素。

【查询任意区间 [i, j] 的最小值】

  • 例：查区间 [4, 9] 的最小值
  • 递归查询到区间 [4, 5]、[6, 8]、[9, 9]，见图中画横线的线段，得最小值 min{6, 2, 10}=2。查询在 O(logn) 时间内完成。
  • 线段树高效的原因：每个结点的值，代表了以它为根的子树上所有结点的值。查询这个子树的值时，不必遍历整棵树，而是直接读这个子树的根。
  • m 次 “单点修改+区间查询” 的总复杂度 O(mlogn)。

3、线段树的树结构

用数组 tree[] 实现一棵满二叉树。每个结点的左右儿子：

左儿子：p<<1，即 p*2。

例：根 tree[1] 的左儿子是 tree[2]，结点 tree[12] 的左儿子是 tree[24]。

右儿子：p<<1|1，即 p*2+1。

例：根 tree[1] 的右儿子是 tree[3]，结点 tree[12] 的右儿子是 tree[25]。

注：p<<1|1，是先左移再按位或

#定义根节点是tree[1]，即编号为1的结点是根
tree=[0]*(N<<2)     #用tree[i]记录线段i的最值
#父子关系，p是父
tree[p<<1]  #左儿子，编号p*2
tree[p<<1|1]    #右儿子，编号p*2+1

【线段树的修改】

点修改：在线段树中每次只修改一个点。

区间修改：每次修改一个区间的所有数。

重点在区间修改

  • 给定 n 个元素 {a1，a2，...，an}：
  • 修改（加）：给定 i,j<=n，把 { ai, ..., aj } 区间内的每个元素加 v。
  • 查询：给定 L,R<=n，计算 {aL, ..., aR} 的区间和。

三、例题应用

1、最大数（lanqiaoOJ题号826）

【题目描述】

维护一个数列，要求提供以下两种操作：

1、查询操作。

语法：Q L

功能：查询当前数列中末尾 L 个数中的最大的数，并输出这个数的值。

限制：L 不超过当前数列的长度。(L>0)

2、插入操作。

语法：A n

功能：将 n 加上 t，其中 t 是最近一次查询操作的答案（如果还未执行过查询操作，则 t=0)，并将所得结果对一个固定的常数 D 取模，将所得答案插入到数列的末尾。

限制：n 是整数 (可能为负数) 并且在长整范围内。

注意：初始时数列是空的，没有一个数。

【输入描述】

第一行两个整数，M 和 D，其中 M 表示操作的个数，D 如上文中所述。接下来的 M 行，每行一个字符串，描述一个具体的操作。语法如上文所述。其中，1<=M<=2×10^5，1<=D<=2×10^9。

【输出描述】

对于每一个查询操作，你应该按照顺序依次输出结果，每个结果占一行。

【完整代码】

N=100001
INF=0x7FFFFFFF
tree=[0]*(N<<2)     #4倍
def bulid(p,pl,pr):     #每一个结点都是极小的一个值
    if pl==pr:
        tree[p]=-INF    #本题是求最大值，把每一个结点赋予极小值
        return
    mid=(pl+pr)>>1
    bulid(p<<1,p1,mid)  #p<<1是左儿子
    bulid(p<<1|1,mid+1,pr)  #p<<1|1是右儿子
    tree[p]=max(tree[p<<1],tree[p<<1|1]) #push_up,这里体现了线段树的一个精髓
def update(p,p1,pr,L,R,d):
    if L<=pl and pr<=R:
        tree[p]=d
        return
    mid=(pl+pr)>>1
    if L<=mid:
        update(p<<1,pl,mid,L,R,d)
    if R>mid:
        update(p<<1|1,mid+1,pr,L,R,d)
    tree[p]=max(tree[p<<1],tree[p<<1|1]) #push_up
    return
def query(p,pl,pr,L,R):
    res=-INF
    if L<=pl and pr<=R:
        return tree[p]
    mid=(pl+pr)>>1
    if L<=mid:
        res=max(res,query(p<<1,pl,mid,L,R))
    if R>mid:
        res=max(res,query(p<<1|1,mid+1,pr,L,R))
    return res

m,D=map(int,input().split())
bulid(1,1,N)    #不用bulid,这样写也行；update(1,1,N,1,N,-INF)
cnt=0
t=0
for i in range(m):
    op=list(input().split())
    if op[0]=='A':
        cnt+=1
        update(1,1,N,cnt,cnt,(int(op[1]+t))%D)
    if op[0]=='Q':
        t=query(1,1,N,cnt-int(op[1])+1,cnt)
        print(t)

（1）初始建一棵空树 build(p, pl, pr)

  • build(p, pl,pr)：p是tree[p]，即建立以 tree[p] 为根的一棵子树，它代表区间 [pl, pr]。
  • build() 函数是一个递归函数，递归到最底的叶子结点，赋初始值 tree[p] = -INF，即一个极小的值。本题是求最大值，把每个结点赋值为极小。
  • 建树用二分法，从根结点开始逐层二分到叶子结点。
  • 作用：把底层的值递归返回，赋值给上层结点。线段树的每个结点，代表了以这个结点为根的子树的最大值 (本题是求最大值，有的题目是求区间和)
  • push_up 利用递归函数的回溯，完成了这一任务。
def bulid(p,pl,pr):     #每一个结点都是极小的一个值
    if pl==pr:
        tree[p]=-INF    #本题是求最大值，把每一个结点赋予极小值
        return
    mid=(pl+pr)>>1
    bulid(p<<1,p1,mid)  #p<<1是左儿子
    bulid(p<<1|1,mid+1,pr)  #p<<1|1是右儿子
    tree[p]=max(tree[p<<1],tree[p<<1|1]) #push_up,这里体现了线段树的一个精髓

初始建树 build() 函数并不是必须的，可以不用。

线段树代码中一定会有一个 update() 函数，作用是更新一个区间，它可以替代 build() 的功能。

（2）更新线段树 update()

update(p, pl, pr, L, R, d) 是通用模板。p 表示结点 tree[p]，pl 是左子树，pr 是右子树。区间 [L, R] 是需要更新的区间。d 是修改或更新。

本题的更新功能是新增一个结点，有两个步骤。

1）把这个结点放在二叉树的叶子上。在本题中这样使用：

update(1, 1, N, cnt, cnt, (x+t)%D)；

作用：把 [cnt, cnt] 区间的值赋值为 (x+t)%D。

因为 [cnt, cnt] 这个区间只包含 tree[cnt] 一个结点，所以它是对新增叶子结点 tree[cnt] 赋值。

2）新增这个结点导致它上层结点的变化，需要把变化上传到上层结点。通过 push_up，把变化递归到上层。

def update(p,p1,pr,L,R,d):
    if L<=pl and pr<=R:
        tree[p]=d
        return
    mid=(pl+pr)>>1
    if L<=mid:
        update(p<<1,pl,mid,L,R,d)
    if R>mid:
        update(p<<1|1,mid+1,pr,L,R,d)
    tree[p]=max(tree[p<<1],tree[p<<1|1]) #push_up
    return

（3）查询

查询区间 [L, R] 的最大值。函数 query(p, pl, pr, L, R) 查询以 p 为根的子树，这棵子树内区间 [L, R] 的最大值。

1）如果这棵子树完全被 [L, R] 覆盖，也就是说这棵子树在要查询的区间之内，那么直接返回 tree[p] 的值。这一步体现了线段树的高效率。如果不能覆盖，那么需要把这棵子树二分，再继续下面两步的查询。

2）如果 L 与左部分有重叠。

3）如果 R 与右部分有重叠。

def query(p,pl,pr,L,R):
    res=-INF
    if L<=pl and pr<=R:
        return tree[p]
    mid=(pl+pr)>>1
    if L<=mid:
        res=max(res,query(p<<1,pl,mid,L,R))
    if R>mid:
        res=max(res,query(p<<1|1,mid+1,pr,L,R))
    return res

2、选数异或（2022年省赛，lanqiaoOJ题号2081）

【题目描述】

给定一个长度为 n 的数列 A1, A2, ...,  An 和一个非负整数 x，给定 m 次查询，每次询问能否从某个区间 [l, r] 中选择两个数使得他们的异或等于 x。

【输入格式】

输入的第一行包含三个整数 n, m, x。第二行包含 n 个整数 A1, A2, ...., An。接下来 m 行，每行包含两个整数 li, ri 表示询问区间 [li, ri]。

【输出格式】

对于每个询问，如果该区间内存在两个数的异或为 x 则输出 yes，否则输出 no。

【评测用例规模与约定】

对于 20% 的评测用例，1<=n,m<=100；

对于 40% 的评测用例，1<=n,m<=1000；

对于所有评测用例，1<=n,m<=100000，0<=x<2^20，1<=li<=ri<=n，0<=Ai<2^20

（1）暴力（%40）

用combinations，遍历 [L,R] 内的任意 2 个数的组合

import itertools
def two(l,r):
    b=itertools.combinations(a[l:r+1],2)
    for i in b:
        if i[0]^i[1]==x:
            return 'yes'
    return 'no'

n,m,x=map(int,input().ssplit())
a=[0]+list(map(int,input().split()))    #a[0]不用
c=[]
for i in range(m):
    c.append(list(map(int,input().split())))
for i in c:
    print(two(i[0],i[1]))

（2）动态规划+字典（100%）

  • 设 ai 右边符合要求的是 aj
  • 设 a(i+1) 右边符合要求的是 ak
  • 若 k<j，则对 ai 来说，它右边的 (ai+1, ak) 这一对数，更好地满足要求。

定义字典 mp，mp 的键是 a[i]，对应的值是 i。

  • 第 7 行：把 a[i] 映射到 i。
  • 第 8~9 行：找到距离 a[i] 的符合题目要求的数的最近位置。
  • 第 10 行：判断查询的区间内，有没有符合要求的两个数。

一次字典操作复杂度是 O(logn)，6行做n次，12行做m次，总复杂度 O(nlogn + mlogn)，能通过 100% 的测试。

n,m,x=map(int,input().split())
a=[0]+list(map(int,input().split()))    #加a[0],从a[1]开始
pos=[0]*(n+10)
pos[n+1]=1<<30
mp={}           #定义字典，字典能把数与位置联系起来
for i in range(n,0,-1):     #n次
    mp[a[i]]=i              #把a[i]映射到i
    y=x^a[i]                #若a^b=c,则b=a^c
    pos[i]=pos[i+1]         #从下一个位置找符合条件的数
    if mp.get(y):
        pos[i]=min(pos[i],mp[y])   #最近位置
for i in range(m):          #m次
    L,R=map(int,input().split())
    if pos[L]<=R:
        print('yes')
    else:
        print('no')

（3）线段树（100%）

区间问题一般用线段树，但是本题的区间查询是任意两个数的异或。

如果能建模为区间最值或区间和，线段树就有效了。

  • 题目是找区间内的 ai⊕aj=x，其中 x 是给定的常数。
  • 变形为对区间内的每个 ai，在区间内找一个 aj=ai⊕x。
  • 对于 ai 来说，可能有多个 aj 满足，显然那个距离它最近的 aj 最好，这样在做任意区间查询的时候，最小的区间查询也能满足。

定义一个数组 Left[]，Left[i] 表示 a[i] 左边最近的等于 ai⊕x 的数 aj 的位置。

本题转换为在区间 [L, R] 内查询一个大于 L 的 Left[i]，a[i]的i显然小于R，此时满足题目要求的一对数是 a[i] 和 a[Left[i]]。

由于那个最大的 Left[i] 肯定满足要求，这样就转换成了查询区间最值问题。

  • 定义 Left[] 时只考虑了 a[i] 左边的数，没有考虑 a[i] 右边的数。这并不会遗漏，因为 a[i] 和它左边的 a[j] 是成对的，对于 a[j] 来说，a[i] 就是右边的数。
  • 如何快速计算 Left[]? 这里利用一个哈希技巧，定义数组pos[]，从左到右遍历 a[] 时，用 pos[k] 记录数字 k 上一次出现的位置，那么 Left[i]=pos[ai⊕x]。
  • 建模为查询区间最值问题后，用线段树编码。每次查询的复杂度为 O(logn)，m 次查询的总复杂度为 O(mlogn)，能通过 100% 的测试。
N=100010
Left=[0]*N
pos=[0]*((1<<20)+10)
tree=[0]*(N<<2)         #4倍
def bulid(p,pl,pr):
    if pl==pr:
        tree[p]=Left[pl]
        return
    mid=(pl+pr)>>1
    bulid(p<<1,pl,mid)  #p<<1是左儿子
    bulid(p<<1|1,mid+1,pr)  #p<<1|1是右儿子
    tree[p]=max(tree[p<<1],tree[p<<1|1])    #push_up
def query(p,pl,pr,L,R):
    if L<=pl and pr<=R:
        return tree[p]
    mid=(pl+pr)>>1
    res=0
    if L<=mid:
        res=max(res,query(p<<1,pl,mid,L,R))
    if R>mid:
        res=max(res,query(p<<1|1,mid+1,pr,L,R))
    return res
n,m,x=map(int,input().split())
a=list(input().split())
a.insert(0,0)           #加一个a[0],从a[1]开始
for i in range(1,n+1):
    a[i]=int(a[i])
    Left[i]=pos[a[i]^x]
    pos[a[i]]=i
bulid(1,1,n)
for i in range(m):
    L,R=map(int,input().split())
    if query(1,1,n,L,R)>=L:
        print('yes')
    else:
        print('no')

以上，线段树的原理和应用

祝好

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/178087.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

反向放大电路并联电容与积分电路并联电阻的区别？

反向放大电路并联电容与积分电路并联电阻的区别？

运放反相比例放大电路中反馈电阻两端经常并联一个电容&#xff0c;而运放积分电路的反馈电容上常常并联一个电阻&#xff0c;两者电路结构相似&#xff0c;如下所示&#xff08;隐去阻容值&#xff09;&#xff0c;二者有何区别呢&#xff1f;电阻、电容分别又起到什么作用&…
阅读更多...
djangorestframework全解

djangorestframework全解

这里写目录标题drf安装与使用ApiView继承自原生View的基类基本使用源码分析drf的Request对象响应模块&#xff08;一般不用管&#xff09;内置渲染器局部使用全局使用解析器&#xff08;一般不用管&#xff09;全局使用解析器局部使用解析器同时使用多个解析器&#xff08;默认…
阅读更多...
雅克比行列式补充和曲面的参数方程求导表示法向量

雅克比行列式补充和曲面的参数方程求导表示法向量

接上篇的雅克比行列式部分。其实对于任何变量x,y, dxdy描述的是一个抽象的“面积”。比如&#xff0c;如果x是力F&#xff0c;y是时间t&#xff0c;那么“面积”Ft其实就是做功。所以我们可以认识到&#xff0c;对于dxdy和dudv之间&#xff0c;如果自变量u&#xff0c;v的改变量…
阅读更多...
【网络安全】ip地址、公网、私网

【网络安全】ip地址、公网、私网

一、IP地址 ip地址相当于收发快递时的收货地址和发货地址 IPV4的地址&#xff1a;192.168.0.1 11000000.10101000.00000000.00000001 windows使用>ipconfig&#xff1b;linux使用ifconfig 可以看到IPV4地址/inet旁边的就是IP地址 IP地址的分类 IP地址有32位&#xff0…
阅读更多...
React事件和原生事件的执行顺序

React事件和原生事件的执行顺序

React在内部对事件做了统一的处理&#xff0c;合成事件是一个比较大的概念 为什么要有合成事件 在传统的事件里&#xff0c;不同的浏览器需要兼容不同的写法&#xff0c;在合成事件中React提供统一的事件对象&#xff0c;抹平了浏览器的兼容性差异React通过顶层监听的形式&am…
阅读更多...
ROS学习寄录之环境搭建

ROS学习寄录之环境搭建

1 创建ROS工作空间 1.1 创建工作空间 &#xff08;1&#xff09;创建工作空间 mkdir catkin_ws &#xff08;2&#xff09;进入catkin_ws文件夹&#xff0c;然后创建一个src文件夹 cd catkin_ws mkdir src &#xff08;3&#xff09;进入src文件夹&#xff0c;生成CMakeL…
阅读更多...
JavaScript typeof

JavaScript typeof

文章目录JavaScript typeof, null, 和 undefinedtypeof 操作符NullUndefinedUndefined 和 Null 的区别JavaScript typeof, null, 和 undefined JavaScript typeof, null, undefined, valueOf()。 typeof 操作符 你可以使用 typeof 操作符来检测变量的数据类型。 实例 typeof …
阅读更多...
2.2 标识符与关键字

2.2 标识符与关键字

文章目录1 标识符2 关键字1 标识符 标识符可以简单的理解成一个名字。 在Java中&#xff0c;我们需要给代码中的很多元素起名&#xff0c;包括类名、方法名、字段名、变量名等等。我们给对应元素起的名称就被称为标识符&#xff0c;一个正确的标识符需要遵循以下规则&#xff…
阅读更多...
【蓝桥杯】简单数论4——丢番图方程

【蓝桥杯】简单数论4——丢番图方程

1、二元线性丢番图方程 方程ax by c被称为二元线性丢番图方程&#xff0c;其中a、b、c是已知整数&#xff0c;x、y是变量,问是否有整数解。 ax by c实际上是二维x-y平面上的一条直线&#xff0c;这条直线上如果有整数坐标点&#xff0c;方程就有解&#xff0c;如果没有整数坐…
阅读更多...
【算法竞赛 5】动态规划 ——— 闫氏DP分析法（从集合角度来分析DP问题——01背包）

【算法竞赛 5】动态规划 ——— 闫氏DP分析法（从集合角度来分析DP问题——01背包）

目录 Description 输入格式 输出格式 数据范围 输入样例 输出样例&#xff1a; 题解 状态表示 状态计算 AC_Code 优化后代码 Description 有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。 第 i 件物品的体积是 vi&#xff0c;价值是 wi。 求解将哪些物品…
阅读更多...
2.4.1 整数型

2.4.1 整数型

文章目录1.整型基本数据类型介绍2.byte 数据类型3.short 数据类型4.int 数据类型5.long 数据类型1.整型基本数据类型介绍 整型用于表示没有小数部分的数字&#xff0c;比如1&#xff0c;2&#xff0c;3等&#xff0c;其允许是负数&#xff0c;JAVA共提供了4种整型数据类型&…
阅读更多...
电阻抗成像OpenEIT 番外篇 简单算法

电阻抗成像OpenEIT 番外篇 简单算法

算法意义 C→Y→V→eC\rightarrow Y \rightarrow V \rightarrow eC→Y→V→e 符号 符号含义–Ω\OmegaΩ研究图像区域∂Ω\partial\Omega∂Ω研究图像区域的边界ϕ(x,y)\phi(x,y)ϕ(x,y)代求电导率σ(x,y)\sigma(x,y)σ(x,y)节点电压 e 电导率jn(x,y)j_n(x,y)jn​(x,y)注入表…
阅读更多...
C++ 多线程12：内存模型(stdmemory_order)

C++ 多线程12：内存模型(stdmemory_order)

cpp 多线程&#xff1a;内存模型(std::memory_order) 文章目录cpp 多线程&#xff1a;内存模型(std::memory_order)概念内存模型基础原子操作间的关系Synchronized-withHappens-beforestd::memory_orderRelaxed orderingRelease-Consume orderingRelease-Acquire orderingSeque…
阅读更多...
UnityEditor编辑器扩展开发-自定义Shader入门

UnityEditor编辑器扩展开发-自定义Shader入门

估计需要自定义Shader 的人不多下面内容就看看作为小白的我们&#xff0c;无从入手&#xff0c;当然首先看看 Amplify Shader Editor(ASE&#xff09;是如何实现Shader定义&#xff0c;从(ASE)的Shader代码&#xff0c;得知自定义原理&#xff08;代码&#xff09;//CustomEdit…
阅读更多...
前端艺术之毛玻璃-倾斜-日历

前端艺术之毛玻璃-倾斜-日历

前端艺术之毛玻璃-倾斜-日历描述项目效果index.htmlindex.css描述 项目描述开发语言HTML、JavaScript、CSS库dyCalendarJS、vanilla-tiltEdge108.0.1462.54 (正式版本) (64 位) 该项目中需要使用到的库有&#xff1a; dyCalendarJS vanilla-tilt.js 是 JavaScript 中的一个平…
阅读更多...
C++ | 哈希 | 基于开散列结构的unordered系列容器模拟实现

C++ | 哈希 | 基于开散列结构的unordered系列容器模拟实现

文章目录unordered_map的封装所有接口的声明与实现operator[]重载unordered_set的封装上篇博客模拟实现了哈希的开散列结构&#xff0c;并且将迭代器与泛型进行了封装&#xff0c;至此我们可以将开散列作为底层结构对STL标准容器——unordered_map和unordered_set进行封装。但是…
阅读更多...
使用Vue 简化 用户查询/添加功能

使用Vue 简化 用户查询/添加功能

使用Vue简化 用户查询/添加功能1. 查询功能1.1 Vue核心对象&#xff1a;1.2 brand.html&#xff1a;1.3 selectAllServlet&#xff08;无变化&#xff09;&#xff1a;2. 添加功能2.1 addBrandhtml&#xff1a;2.2 Vue核心对象&#xff1a;2.3 addServlet&#xff08;无变化&am…
阅读更多...
网关zuul源码解析==ZuulServlet

网关zuul源码解析==ZuulServlet

用法&#xff1a; 使用zuul网关&#xff0c;需要引入starter为 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-zuul</artifactId> </dependency> 同时在springboot启动类上加注解…
阅读更多...
7、代码模板的使用

7、代码模板的使用

文章目录7、代码模板的使用7.1 查看Postfix Completion模板&#xff08;后缀补全&#xff09;7.2 查看Live Templates模板&#xff08;实时模板&#xff09;7.3 常用代码模板1 非空判断2 遍历数组和集合3 输出语句4 对象操作5 静态常量声明7.4 自定义代码模板1 自定义Postfix C…
阅读更多...
Android入门第60天-MVVM中的Databinding与ListView结合使用

Android入门第60天-MVVM中的Databinding与ListView结合使用

开篇 还记得我们进入Listview、GridView都是以一个layoutadapter组合在一起来实现的是吧&#xff1f;那么还记得我们的Adapter的写法么&#xff1f; 在我们的Adapter里提供了一个bindView方法 。 在调用时我们需要在Activity里把layout里的控件元素一个个传给这个Adapter。 在我…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023