目录
Description
输入格式
输出格式
数据范围
输入样例
输出样例:
题解
状态表示
状态计算
AC_Code
优化后代码
Description
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
题解
每个物品只有两种状态,选或者不选,选法数量就是2的n次方种。
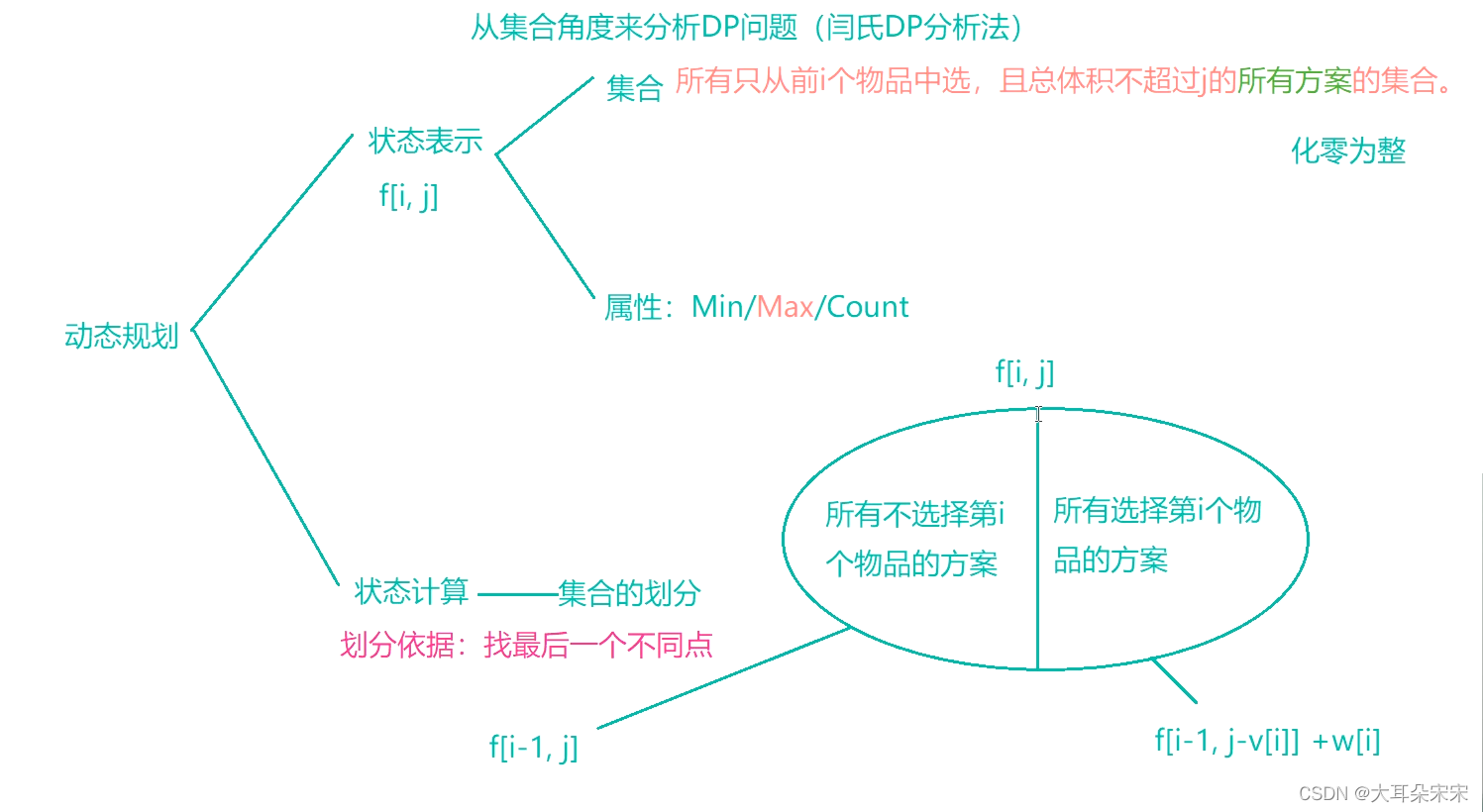
状态表示
一般是第一维是选取前 i 个物品,后面几维是限制条件
集合 :所有只考虑前 i 个物品,且总体积不大于 j 的选法的集合。
属性 :集合中每个方案的max
状态计算
集合划分(如图)
1、不重复
2、不遗漏
AC_Code
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N];//分别表示体积和价值
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++)
for(int j = 0;j <= m; j ++)
{
f[i][j] = f[i - 1][j];//左半边的子集
if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
优化后代码
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N];
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i ++ )
{
int v, w;
cin >> v >> w;
for (int j = m; j >= v; j -- )
f[j] = max(f[j], f[j - v] + w);
}
cout << f[m] << endl;
return 0;
}