数组的基本概念

数组应用实例:统计随机数

数组应用实例:直方图

字符串

多维数组

数组的基本概念

数组(Array)也是一种复合数据类型，它由一系列相同类型的元素(Element)组成。例如定义一个由4个int型元素组成的数组count:

int count[4];

和结构体成员类似，数组count的4个元素的存储空间也是相邻的。结构体成员可以是基本数据类型，也可以是复合数据类型，数组中的元素也是如此。根据组合规则，我们可以定义一个由4个结构体元素组成的数组:

struct complex_struct
{
  double x,y;
}a[4];

也可以定义一个包含数组成员的结构体:

struct 
{
  double x,y;
  int count[4];
}a;

 数组类型的长度应该是用一个整数常量表达式来指定，数组中的元素通过下标来访问。例如前面定义的由4个int型元素组成的数组count图示如下:

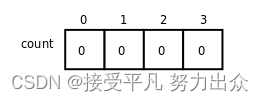
 整个数组占了4个int型的存储单元，存储单元用小框表示，里面的数字是存储在这个单元中的数据，而框外面的数字是下标，这四个单元分别用count[0],count[1],count[2],count[3]来访问。注意，在定义数组int count[4]时,方括号中的数字4表示数组的长度，而在访问数组时，方括号中的数字表示访问数组的第几个元素。和我们平常数数不同，数组元素是从"第0个"开始数的，大多数编程语言都是这么规定的，所以计算机术语中有Zeroth这个词。这样规定使得访问数组元素非常方便，比如count数组中的每个元素占4个字节，则count[i]表示从数组开头跳过4*i个字节之后的那个存储单元，这种数组下标的表达式不仅可以表示存储单元中的值，也可以表示存储单元本身，也就是说可以做左值，因此一下语句都是正确的:

count[0]=7;
count[1]=count[0]*2;
++count[2];

到目前为止我们学了五种后缀运算符:后缀++，后缀--，结构体取成员.,数组取下标[]，函数调用()，还学习了五种单目运算符(前缀运算符):前缀++，前缀--，正号+，负号-，逻辑非!。在C语言中后缀运算符的优先级最高，单目运算符的优先级仅次于后缀运算符，比其它运算符的优先级都高，所以上面举例的++count[2]应该看作对count[2]做前缀++运算。

数组下标也可以是表达式，但表达式的值必须是整型的。例如:

int i=10;
count[i]=count[i+1];

 使用数组下标不能超出数组的长度范围，这一点在使用变量做数组下标时要注意。C编译器并不检查count[-1]或是count[100]这样的访问越界错误，编译时能顺利通过，所以属于运行时错误。但有时候这种错误很隐蔽，发生访问越界时程序可能并不会立即崩溃，而执行到后面某个正确的语句时却有可能突然崩溃，所以从一开始写代码就要小心避免出现这样的问题，事后依靠调试来解决问题的成本是很高的。

数组也可以像结构体一样初始化，未赋值的元素也是用0来初始化的，例如:

int count[4]={3,2,};

则count[0]等于3，count[1]等于2，后面的两个元素等于0.如果定义数组的同时初始化它，也可以不指定数组的长度，例如:

int count[]={3,2,1,};

 编译器会根据Initalizer有三个元素确定数组的长度为3.利用C99的新特性也可以做出Memberwise Initalization:

int count[4]={[2]=3};

下面来举一个完整的例子:

#include<stdio.h>
int main(void)
{
  int count[4]={3,2,},i;
  for(i=0;i<4;i++)
     printf("count[%d]=%d\n",i,count[i]);
  return 0;
}

 这个例子通过循环把数组中的每个元素依次访问一遍，在计算机术语中成为遍历。注意控制表达式i<4,如果写成i<=4就错了，因为count[4]是访问越界的。

数组和结构体虽然有很多相似之处，但也有一个显著的不同:数组不能相互赋值或初始化，例如这样是错误的:

int a[5] = { 4, 3, 2, 1 };
int b[5] = a;

 相互赋值也是错的:

a = b;

既然不能相互赋值，也就不能用数组类型作为函数的参数或返回值。如果写出这样的函数定义:

void foo(int a[5])
{
    ...
}

 然后这样调用:

int array[5] = {0};
foo(array);

编译器也不会报错，但这样写并不是传一个数组类型参数的意思。对于数组类型有一条特殊规则:数组类型做右值使用时，自动转换成指向数组首元素的指针。所以上面的函数调用其实是传一个指针类型的参数，而不是数组类型的参数。接下来的几章里有的函数需要访问数组，我们就把数组定义为全局变量给函数访问，等以后讲了指针再使用传参的方法。这也解释了为什么数组类型不能相互赋值或初始化，例如上面提到的a=b这个表达式，a和b都是数组类型的变量，但是b做右值使用，自动转换成指针类型，而左边仍然是数组类型，所以编译器报的错是是error: incompatible

types in assignment。

数组应用实例:统计随机数

本节通过一个实例介绍使用数组的一些基本模式。问题是这样的:首先生成一系列0-9的随机数保存在数组中，然后统计其中每个数字出现的次数并打印，检查这些数字的随机性如何。随机数在某些场合(例如游戏程序)是非常有用的，但是用计算机生成完全随机的数并不是那么容易的。计算机执行每一条指令的结果都是非常确定的，没有一条指令产生的是随机数，调用C标准库得到的随机数其实是伪随机数，使用数学公式算出来的确定的数，只不过这些数看起来是比较随机的，并且从统计意义上也是很接近均匀分布的随机数。

C标准库中生成伪随机数的是rand函数，使用这个函数需要包含stdlib.h头文件，他没有参数，返回值是一个介于0和RAND_MAX之间的接近均匀分布的整数。RAND_MAX是该头文件中定义的一个常量，在不同的平台上有不同的取值，但可以肯定的它是一个非常大的整数。通常我们用到的随机数是限定在某个范围之中的，例如0-9，而不是0-RAND_MAX，我们可以用%运算符将rand函数的返回值处理一下:

int x = rand() % 10;

完整的程序如下:

#include<stdio.h>
#include<stdlib.h>
#define N 20
int a[N];
void g_random(int upper)
{
	for (int i = 0; i < N; i++)
	{
		a[i] = rand() % upper;
	}
}
void print_random()
{
	for (int i = 0; i < N; i++)
	{
		printf("%d ", a[i]);
	}
}
int main(void)
{
	g_random(10);
	print_random();
	return 0;
}

运行结果如下:

这里介绍一个新的语法， 用#define定义一个常量。实际上编译器的工作分为两个阶段，先是预处理阶段，然后才是编译阶段，用gcc的-E选项可以看到预处理之后，编译之前的程序:

$ gcc -E main.c
...（这里省略了很多行stdio.h和stdlib.h的代码）
int a[20];
void gen_random(int upper_bound)
{
 int i;
 for (i = 0; i < 20; i++)
 a[i] = rand() % upper_bound;
}
void print_random()
{
 int i;
 for (i = 0; i < 20; i++)
 printf("%d ", a[i]);
 printf("\n");
}
int main(void)
{
 gen_random(10);
 print_random();
 return 0;
}

 可见在这里预处理器做了两件事情，一是把头文件stdio.h和stdlib.h在代码中展开，二是把#define定义的标识符N替换成它定义20(在代码中做了三处替换，分别位于数组的定义中的两个函数中)。像#include和#define这种以#号开头的行称为预处理指示，我们将在后面预处理学习其他预处理指示。此外，用cpp main.c命令也可以达到同样的效果，只做预处理而不编译，cpp表示C preprocessor。

那么用#define定义的常量和枚举常量有什么区别?首先,define不仅用于定义常量，也可以定义更复杂的语法结构，称为宏定义。其次，define定义是在预处理阶段处理的，而枚举是在编译阶段处理的。

#include <stdio.h>
#define RECTANGULAR 1
#define POLAR 2
int main(void)
{
 int RECTANGULAR;
 printf("%d %d\n", RECTANGULAR, POLAR);
 return 0;
}

注意，虽然include和define在预处理指示中有特殊含义，但他们并不是C语言的关键字，换句话说, 它们也可以用作标识符，例如声明int include;或者void define(int);在预处理阶段，如果一行以#号开头，后面跟着include或define,预处理器就认为这是一条预处理指示，除此之外出现在其他地方的include或define预处理器并不关心，只是当作一个普通标识符交给编译阶段去处理。

回到随机数这个程序继续讨论，一开始为了便于分析和调试，我们取小一点的数组长度，只生成20个随机数，这个程序的运行结果:

3 6 7 5 3 5 6 2 9 1 2 7 0 9 3 6 0 6 2 6

看起来很随机了，但随机性如何?分布的均匀吗?所谓均匀分布，应该每个数出现的概率都是一样的。在上面的20个结果中，6出现了5次，而4和8一次也没出现。但这并说明不了什么，毕竟我们的样本太少了，才20个数，如果足够的，比如说1000000个数，统计一下其中的数字才能去说明问题。但总不能都把这些数打印出来挨个去数吧。我们需要写一个函数统计每个数字出现的次数。完整的程序如下:

#include <stdio.h>
#include <stdlib.h>
#define N 100000
int a[N];
void gen_random(int upper_bound)
{
 int i;
 for (i = 0; i < N; i++)
 a[i] = rand() % upper_bound;
}
int howmany(int value)
{
 int count = 0, i;
 for (i = 0; i < N; i++)
 if (a[i] == value)
 ++count;
 return count;
}
int main(void)
{
 int i;
 gen_random(10);
 printf("value\thow many\n");
 for (i = 0; i < 10; i++)
 printf("%d\t%d\n", i, howmany(i));
 return 0;
}

 我们只要把#define N的值改为100000，就相当于把整个程序中所用到N的地方都改了，如果我们不这样写，而是在定义数组时直接写成int a[20]。在每个循环中也直接使用20这个值，这称为硬编码，如果原来的代码是硬编码的，那么一旦需要把20改成100000就非常麻烦了，你需要遍历整个d代码去找，判断哪些20表示这个数组的长度就改为100000，哪些20表示别的数量则不做改动，如果代码很长，这是很容易出错的。所以，写代码时应尽可能避免硬编码，这其实也是一个"提取公因式"的过程，和前面的数据抽象讲的抽象具有相同的作用，就是避免一个地方的改动涉及到大的范围，这个程序的运行结果如下:

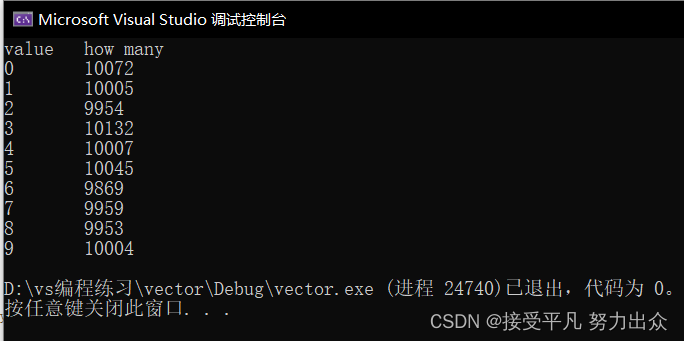
各个数字出现的次数都在10000次左右，可以看出来是比较均匀的。 

思考:用rand函数生成[10, 20]之间的随机整数，表达式应该怎么写？

解题思路:10~20共有11个数字，所以是 rand()%11+10；

数组应用实例:直方图

继续上面的例子，我们统计一列0-9的随机数，打印每个数字出现的次数，像这样的统计结果称为直方图。有时候我们并不是只想打印，更想把统计结果保存下来以便做后续处理。

我们可以把程序改成这样:

int main(void)
{
 int howmanyones = howmany(1);
 int howmanytwos = howmany(2);
 ...
}

这显然是太繁琐，要是这样地随机数有100个?显然这里用数组最合适不过了:

int main(void)
{
 int i, histogram[10];
 gen_random(10);
 for (i = 0; i < 10; i++)
 histogram[i] = howmany(i);
 ...
}

 有意思的是，这里的循环变量i有两个作用，一是作为参数传给howmany函数，统计数字i出现地次数，二是做histogram地下标，也就是"把数字i出现地次数保存在数组histogram的第i个位置"。

尽管上面的方法可以准确地得到统计结果，但是效率很低，这100000个随机数需要从头到尾检查十遍，每一遍只统计一种数字地出现次数。其实可以把histogram中的元素当作累加器来用，这些随机数只需从头到尾检查一遍就可以得出结果:

int main(void)
{
 int i, histogram[10] = {0};
 gen_random(10);
 for (i = 0; i < N; i++)
 histogram[a[i]]++;
 ...
}

首先把histogram的所有元素初始化为0，注意使用局部变量的值之前一定要初始化，否则值不正确的。接下来的代码很有意思，在每次循环中，a[i]就是出现的随机数，而这个随机数同时也是histogram的下标，这个随机数每出现一次就把histogram中相应的元素加1

把上面的程序运行几遍，你会发现每次产生的随机数都是一样的，不仅如此，在别的计算机上运行该程序产生的随机数很可能也是这样。这正说明这些数是伪随机数，是用一套确定的公式基于某个初值算出来的，只要初值相同，随后的整个数列都相同。实际应用中不可能使用每次都一样的随机数，例如开发一个麻将游戏，每次运行这个游戏摸到的牌不应该是一样的。因此，C标准库允许我们自己指定一个初值，然后在此基础上生成伪随机数，这个初值称为Seed，可以用srand函数指定Seed.

srand((unsigned)time(NULL))

srand函数是随机数发生器的初始化函数。

原型:

void srand(unsigned seed);

用法: 它初始化随机种子，会提供一个种子，这个种子会对应一个随机数，如果使用相同的种子后面的 rand() 函数会出现一样的随机数，如: srand(1); 直接使用 1 来初始化种子。不过为了防止随机数每次重复，常常使用系统时间来初始化，即使用 time函数来获得系统时间，它的返回值为从 00:00:00 GMT, January 1, 1970 到现在所持续的秒数，然后将time_t型数据转化为(unsigned)型再传给srand函数，即: srand((unsigned) time(&t)); 还有一个经常用法，不需要定义time_t型t变量,即: srand((unsigned) time(NULL)); 直接传入一个空指针，因为你的程序中往往并不需要经过参数获得的数据。

进一步说明下：计算机并不能产生真正的随机数，而是已经编写好的一些无规则排列的数字存储在电脑里，把这些数字划分为若干相等的N份，并为每份加上一个编号用srand()函数获取这个编号，然后rand()就按顺序获取这些数字，当srand()的参数值固定的时候，rand()获得的数也是固定的，所以一般srand的参数用time(NULL)，因为系统的时间一直在变，所以rand()获得的数，也就一直在变，相当于是随机数了。只要用户或第三方不设置随机种子，那么在默认情况下随机种子来自系统时钟。如果想在一个程序中生成随机数序列，需要至多在生成随机数之前设置一次随机种子。

即：只需在主程序开始处调用 srand((unsigned)time(NULL)); 后面直接用rand就可以了。不要在 for 等循环放置 srand((unsigned)time(NULL));

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
 
int main()
{
   int i, n;
   time_t t;
   
   n = 5;
   
   /* 初始化随机数发生器 */
   srand((unsigned) time(&t));
 
   /* 输出 0 到 50 之间的 5 个随机数 */
   for( i = 0 ; i < n ; i++ ) {
      printf("%d\n", rand() % 50);
   }
   
  return(0);
}

运行结果:

思考:定义一个数组，编程打印它的全排列。比如定义：

#define N 3
int a[N] = { 1, 2, 3 };

则运行结果是：

$ ./a.out
1 2 3 
1 3 2 
2 1 3 
2 3 1 
3 2 1 
3 1 2 
1 2 3

思路:

1. 把第1个数换到最前面来（本来就在最前面），准备打印1xx，再对后两个数2和3做全排列。
2. 把第2个数换到最前面来，准备打印2xx，再对后两个数1和3做全排列。
3. 把第3个数换到最前面来，准备打印3xx，再对后两个数1和2做全排列。

#include <stdio.h>
#define N 3
 
int a[N];
 
void perm(int); /*求数组的全排列 */
void print();
void swap(int, int);
 
int main(){
    int i;
    for(i = 0; i < N; ++i){
        a[i] = i + 1;
    }
    perm(0);
}
 
void perm(int offset){
    int i, temp;
    if(offset == N-1){  // BaseCase
        print();
        return;
    }else{
        for(i = offset;i < N; ++i){
            swap(i, offset);//交换前缀
            perm(offset + 1);//递归
            swap(i, offset);//将前缀换回来，继续做前一次排列
        }
    }
}
 
void print(){
    int i;
    for(i = 0; i < N; ++i)
        printf(" %d ",a[i]);
    printf("\n");
}   
 
void swap(int i, int offset){
    int temp;
    temp = a[offset];
    a[offset] = a[i];
    a[i] = temp;
}

字符串

之前我一直对字符串避而不谈，不做详细解释，现在已经具备了必要的基础知识，可以深入讨论一下字符串了。字符串可以看做一个数组，它的每个元素都是字符型的，例如字符串"Hello,world!\n"图示如下:

注意每个字符末尾都有一个字符'\0‘做结束符，这里的\0是ASCll码的八进制表示，也就是ASCII码为0的NUII字符，在C语言中这种字符串也称为以零结尾的字符串。数组元素可以用过数组名加下标的方式访问，而字符串字面值也可以像数组名一样使用，可以加下标访问其中的字符:

char c = "Hello, world.\n"[0];

但是通过下标修改其中的字符是不允许的:

"Hello, world.\n"[0] = 'A';

 这行代码会产生编译错误,说字符串字面值是只读的,不允许修改的。字符串字面值还有一点和数组明类似，做右值使用时自动转换成指向首元素的指针，在形参和实参中我们看到printf原型的第一个参数是指针类型，而printf("hello world");其实就是传一个指针参数给printf.

前面讲过数组可以像结果提一样初始化，如果是字符数组，也可以用一个字符串字面值来初始化:

char str[10] = "Hello";

 相当于:

char str[10] = { 'H', 'e', 'l', 'l', 'o', '\0' };

str的后四个元素没有定，自动初始化为0，即NUII字符。注意，虽然字符串字面值"Hello"是只读的，但用它初始化的数组str却是可读可写的。 数组str中保存了一串字符，以'\0’结尾，也可以叫字符串。在本书中只要是以NUII字符结尾的一串字符都叫字符串，不管是像str这样的数组，还是像"Hello"这样的字符串字面值。

如果用于初始化的字符串字面值比数组还长，比如:

char str[10] = "Hello, world.\n";

则数组str只包含字符串的前10个字符，不包含NUII字符，这种情况编译器会给出警告。如果要用一个字符串字面值准确地初始化一个字符数组，最好的办法是不指定数组长度，让编辑器自己计算:

char str[] = "Hello, world.\n";

char str[14] = "Hello, world.\n";

printf("string: %s\n", "Hello");

printf("string: Hello\n");

printf("string: %s\n", str);

多维数组

就像结构体可以嵌套一样，数组也是可以嵌套的，一个数组的元素可以是另外一个数组，这样就构成了一个多维数组。例如定义并初始化一个二维数组:

int a[3][2] = { 1, 2, 3, 4, 5 };

 数组a有三个元素，a[0],a[1],a[2]。每个元素也是一个数组，例如a[0]是一个数组，它有两个元素是a[0][0],a[0][1]，这两个元素的类型是int,值分别是1,2.同理，数组a[1]的两个元素是3,4.数组a[2]的两个元素是5,0。如下图所示:

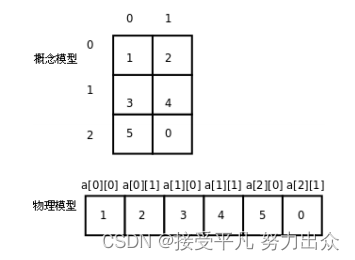
 从概念模型上看，这个二维数组是三行两列的表格，元素的两个下标分别是行号和列号。从物理模型上看，这六个元素在存储器中仍然是连续存储的，就像一维数组一样，相当于把概念模型的表格一行行接起来拼成一串，C语言的这种存储方式称为Row_major方式，而有些编程语言是把概念模型的表格一列一列的接起来拼成一串存储的，称为Column_major方式。

多维数组也可以像嵌套结构体一样用嵌套初始化，例如上面的二维数组也可以这样初始化:

int a[][2] = { { 1, 2 },
               { 3, 4 },
               { 5, } };

注意，除了第一维的长度可以由编译器自动计算而不需要指定，其余各维都必须明确指定长度。利用C99的新特性也可以做Memberwise Initialization,例如:

int a[3][2] = { [0][1] = 9, [2][1] = 8 };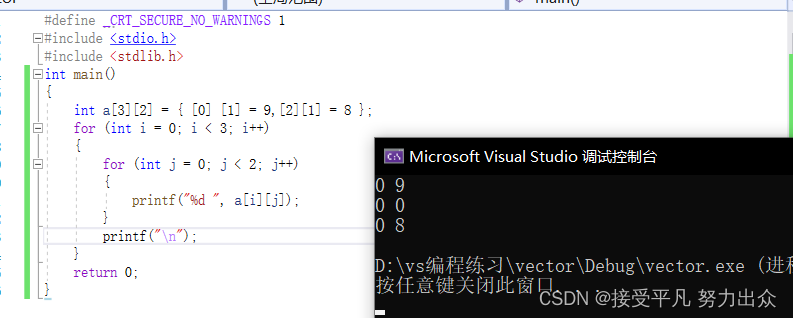

 结构体和数组嵌套的情况也可以做Memberwise Initalization,例如:

struct complex_struct {
 double x, y;
} a[4] = { [0].x = 8.0 };
struct {
 double x, y;
 int count[4];
} s = { .count[2] = 9 };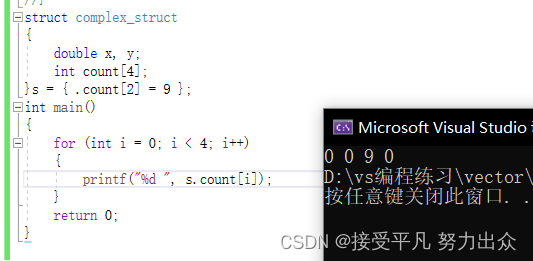

 如果是多维字符数组，也可以嵌套使用字符串字面值做Initalizer,例如:

#include <stdio.h>
void print_day(int day)
{
 char days[8][10] = { "", "Monday", "Tuesday",
 "Wednesday", "Thursday", 
"Friday",
 "Saturday", "Sunday" };
 if (day < 1 || day > 7)
 printf("Illegal day number!\n");
 printf("%s\n", days[day]);
}
int main(void)
{
 print_day(2);
 return 0;
}

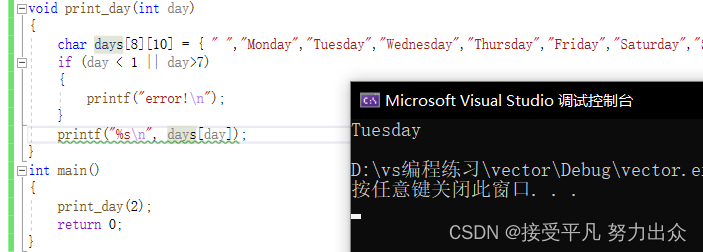
多维字符数组

 这个程序中定义了一个多维字符数组char days[8][10];为了使1-7刚好映射到days[1]-days[7]，我们把days[0]空出来不用，所以第一维的长度是8，为了使最长的字符串"Wednesday"能够保存在一行，末尾还能多出个NULL字符位置，所以第二维长度是10。这个程序和前面switch语句的功能其实是一样的，但是代码简洁太多了。简洁的代码不仅可读性强，而且维护成本也低。像switch语句那样一堆case,printf和break，如果漏写一个break就要出现Bug。这个程序之所以简洁，是因为用数据代替了代码。具体来说，通过下标访问字符串组成的数组可以代替一堆case分支判断，这样就可以把每个case里重复的代码(printf调用)提取出来，从而又一次达到了"提取公因式"的效果。这种方法称为数据驱动的编程，写代码最重要的是选择正确的数据结构来组织信息，设计控制流程和算法尚在其次，只要数据结构选择的正确，其他代码自然而然就变得容易理解和维护了，就像这里的printf自然而然就被提取出来了。

最后，综合本章知识，写一个简单的小游戏--剪刀石头布:

#include<stdio.h>
#include<stdlib.h>
#include<time.h>

int main()
{
	char gesture[3][10] = { "scissor","stone","cloth" };
	int man, computer, result, ret;
	srand((unsigned)time(NULL));
	while (1)
	{
		computer = rand() % 3;
		printf("Input your gesture(0-scissor 1-stone 2-cloth):\n");
		ret = scanf("%d", &man);
		if (ret != 1 || man < 0 || man>2)
		{
			printf("Invalid input! Please input 0,1or2\n");
			continue;
		}
		printf("Your gesture:%s\tComputer's gesture:%s\n", gesture[man], gesture[computer]);
		result = (man - computer + 4) % 3 - 1;
		if (result > 0)
		{
			printf("You win!\n");
		}
		else if (result == 0)
		{
			printf("Draw!\n");
		}
		else
		{
			printf("You lose!\n");
		}
	}
	return 0;
}

运行结果:

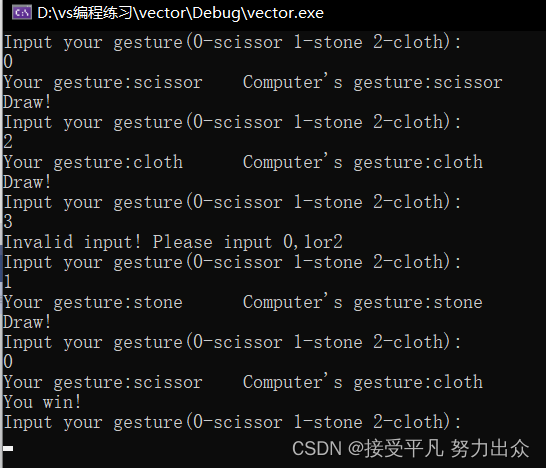
 0，1，2三个整数分别是剪刀石头布在程序中的内部表示,用户也要求输入0，1，2。然后和计算机随机生存的0，1，2比胜负。这个程序的主体是一个死循环，需要按Ctrl-c退出。以往我们写的程序只能打印输出，在这个程序中我们第一次碰到处理用户输入的情况。我们简单介绍一下scanf函数的用法，到格式化I/O函数中再详细解释。scanf("%d",&man)这个调用的功能是等待用户输入一个整数并回车，这个整数会被scanf函数保存在man这个整型变量里。如果用户输入合法(输入的确实是数字而不是别的字符)，而scanf函数返回1.表示成功读入一个数据。但即使用户输入的是整数，我们还需要进一步检查是不是在0-2的范围内，写程序时对用户输入要格外小心，用户有可能输入任何数据，他才不管游戏规则是什么.

和print类似，scanf也可以用%c,%f,%s等转换说明。如果在传给scanf的第一个参数中用%d,%f或%c表示读入一个整数，浮点数或字符，则第二个参数的形式应该是&运算符加相应类型的变量名,表示读进来的数保存到这个变量中，&运算符的作用是得到一个指针类型，到后面指针的基本概念再详细解释；如果在第一个参数中用%s读入一个字符串，则第二个参数应该是数组名，数组名前面不加&，因为数组类型做右值自动转换成指针类型，在端点章节中有scanf读入字符串的例子。

思考:(man-computer+4)%3-1这个神奇的表达式是如何比较出0，1，2这三个数字在"剪刀石头布"意义上的大小?

胜 负 平 胜 负
man-computer -2 -1 0 1 2
man-computer+4 2 3 4 5 6
(man-computer+4)%3 2 0 1 2 0
(man-computer+4)%3-1 1 -1 0 1 -1

刀石头布相生相克，形成一个环，凡是具有环的特性的数学模型都可以考虑用取模运算，首先确定了man-computer和%3，然后再调整其它常数得到normalized的结果。