整数惟一分解定理

任何一个大于1的整数n都可以分解成若干个质因数（素因数）的连乘积，如果不计各个素因数的顺序，那么这种分解是唯一的，即若n>1，一定存在：n=p1p2p3…pm（p1.p2.均为n的质因数）

上式常记作：
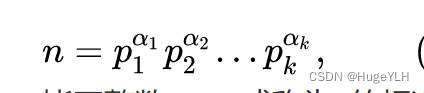
在这里插入图片描述
称为n的标准分解式，质因数分解式。

对于n的标准分解式来说：根据n的标准分解式可以得到以下结论！！！！很重要！！！

可求得n的所有因子个数：(a1+1)(a2+1)(a3+1…+ak+1)
n的所有因子之和：对每个质因数计算由0次至最高次方幂的和，最后把得到的数相乘就得到n的所有因子的和.

在这里插入图片描述

注意：这两个结论非常重要！！！！！！！！！！

再次回到题目：让我们求x^y，因此x的标准分解式如上图所示，我们计算x的y次方，实际上就是计算x的标准分解式的y次方！！！！！！！！！！！

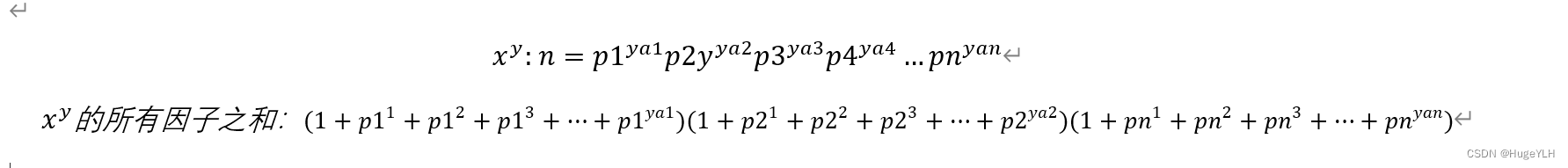
在这里插入图片描述
因此题目让我们求x^y的所有因子之和取余9901，因此这道题就是让我们求：

上图中x^y的所有因子之和然后取余p的结果。，我们只要求得上面的那个长式子的值即可，这个长式子其实就是等比数列求和，因为它的每一个括号里都是一个等比数列的项

我们的基本思路就已经完成了，即我们现在的问题就是如何求得 x^y 的所有因子之和的那一串长式子，即等比数列的和。

可以看出：

1+p1^1+ p1^2+ p1^3 +… p1^n
1+p2^1+ p2^2+ p2^3 +… p2^n
1+pn^1+ pn^2+ pn^3 +… pn^n

他们都具有相同的结构，即
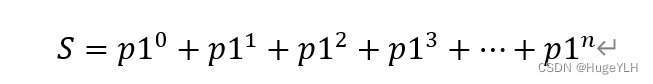
在这里插入图片描述

但是如何求出这个等比数列的和呢?

分治法求等比数列和

我们采用分治法求等比数列的和，我们首先来给这个S举一个例子：
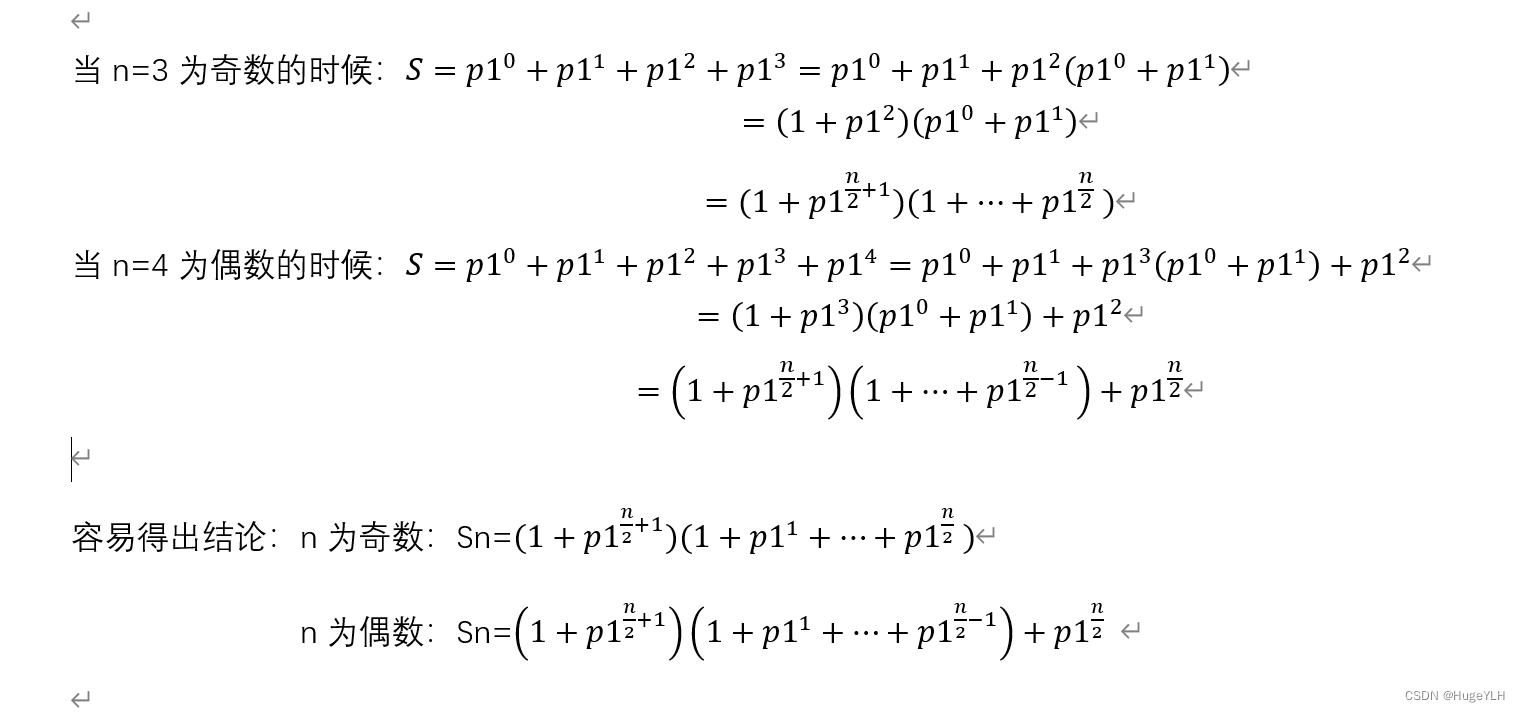
在这里插入图片描述

因此我们就可以得到S的计算公式，分别为n是奇数的情况和n是偶数的情况。而我们注意到，在Sn的式子中，我们又可以得到（1+p1^1+… +p1^(n/2)）这样一个式子，和我们一开始的S的式子形状类似：所以我们便可以通过递归求解中间第二个长式子，而我们可以通过快速幂求得第一个括号里的短式子：(1+ p1^(n/2+1))，而我们要求这一个Sn，只需要传递一个n参数(位数)和p1参数(底数)。

分治求快速幂的模板：注意求和之后要取mod

//分治求快速幂
LL sum(int n,int p1)
{
	if (n == 0)return 1;
	if (n & 1)
	{
		//n是奇数
		return (1 + qpow(p1, n / 2 + 1)) * sum(n / 2, p1) % p;
	}
	else
	{
		//n是偶数
		return (1 + qpow(p1, n / 2 + 1)) * (sum(n / 2 - 1, p1)) % p + qpow(p1, n / 2) % p;
	}
}

完整代码

之和，我们便可以求出x的每一个质因子，以及这个质因子所出现的次数，然后带入sum中，求出x^y 的每一个质因子的连乘积，一直乘到x<=1便得到了答案，注意几个细节：

代码中出现的所有数据类型最好使用long long 型，因此即使是一个统计某一个质因子的出现的次数 Cnt也应该是一个long long
注意所有式子中%p的顺序：在n为奇数的式子最后%p，在n为偶数的式子的中间%p，后面还有一个快速幂的式子也要%p（具体的我也不知道，反正%肯定没坏处）。另外ans在计算每一项式子得到答案的时候要一项一项的乘，然后%p，不能让ans乘以（…%p）的式子，即不能写成： ans*= … 这样写ans会超出数据范围，因为ans本身并没有%p。

#include <iostream>
#include <cmath>
using namespace std;

typedef long long LL;
const LL p = 9901;
int x, y;
LL qpow(LL a, LL b)
{
	/*
	快速幂
	*/
	LL res = 1 % p;
	for (; b; b >>= 1)
	{
		if (b & 1)
		{
			res = res * a % p;
		}
		a = a * a % p;
	}
	return res;
}
//分治求快速幂
LL sum(int n,int p1)
{
	/*
	n：项数
	p1：底数
	*/
	if (n == 0)return 1;
	if (n & 1)
	{
		//n是奇数
		return (1 + qpow(p1, n / 2 + 1)) * sum(n / 2, p1) % p;
	}
	else
	{
		//n是偶数
		return ((1 + qpow(p1, n / 2 + 1)) * (sum(n / 2 - 1, p1)) % p + qpow(p1, n / 2) % p);
	}
}
int main()
{
	LL ans = 1;
	cin >> x >> y;	//x^y
	for (int i = 2; i <= sqrt(x); i++)
	{
		int cnt = 0;
		if (x % i == 0)
		{
			while (x % i == 0)
			{
				x /= i;
				cnt++;
			}
			//i：就是x的某一个质因子			
			//cnt：就是x的某个质因子的幂次  cnt*y 就是x^y的质因子的连乘积的某一项
		}
		//n的所有因子之和的每一项: ans依次相乘
		ans *=sum(cnt * y, i) % p;
	}
	if (x > 1)
	{
		ans *=sum(y, x) % p;
	}
	cout << ans;
	return 0;
}