下面用C语言介绍堆的实现以及应用

1. 堆的简介

堆是一颗完全二叉树。这里所说的堆是一种非连续的数据结构，与操作系统内存分布的堆是两回事，它们没有任何联系。
堆有以下特点：

1. 堆中某个结点的值总是不大于或不小于其父结点的值
2. 堆是一颗完全二叉树
3. 堆的逻辑结构是一颗完全二叉树，但是物理结构是顺序表

小堆： 任何一个结点的值都大于或者等于孩子结点的值
小堆： 任何一个结点的值都小于或者等于孩子结点的值

数据下标计算父子关系公式

2. 堆的实现

这些介绍堆的以下接口

HeapInit

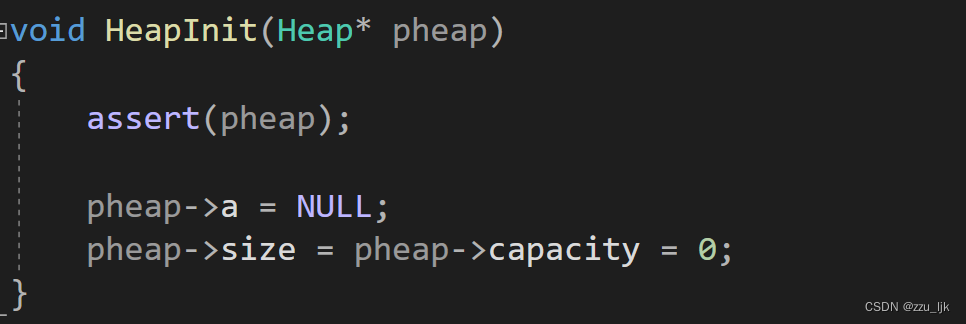
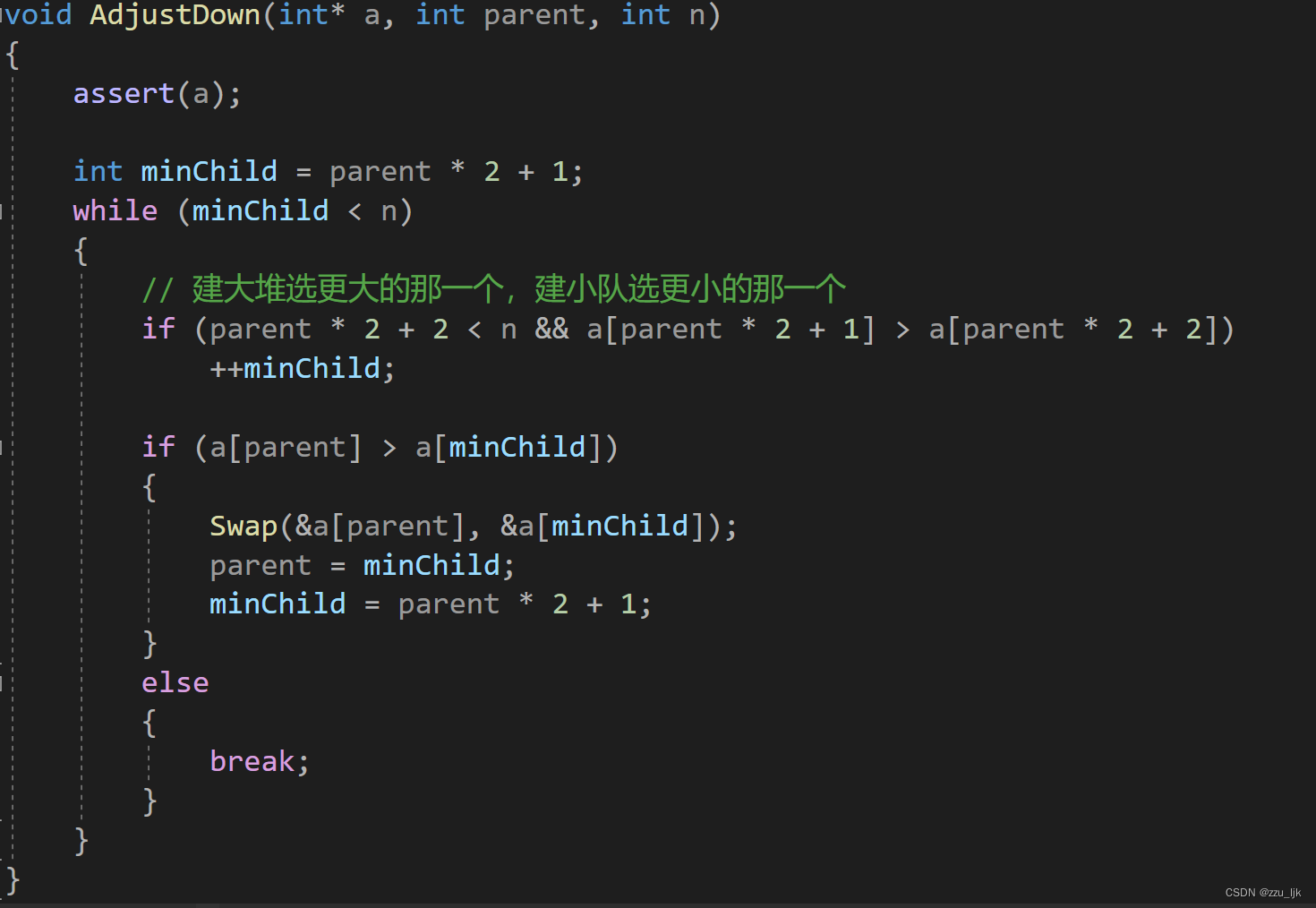
HeapDestroy

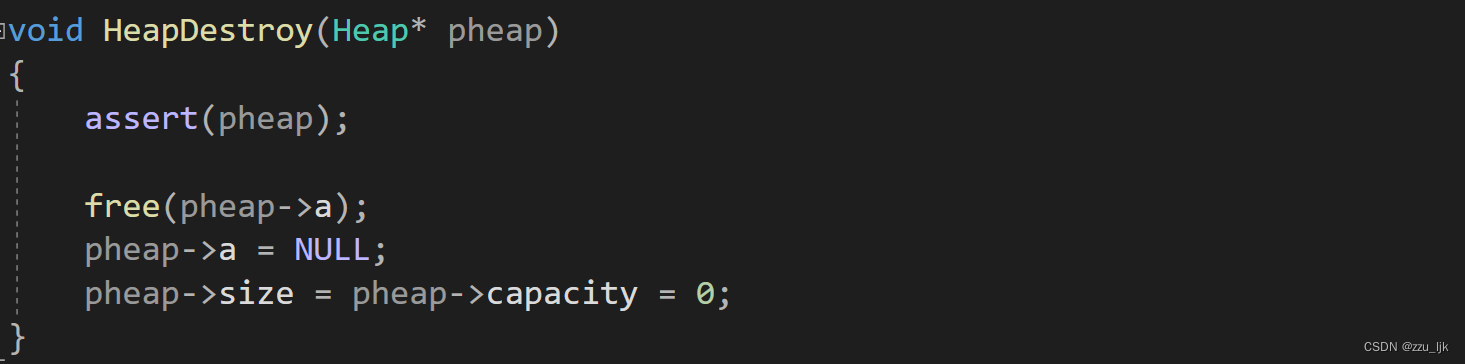
HeapPush

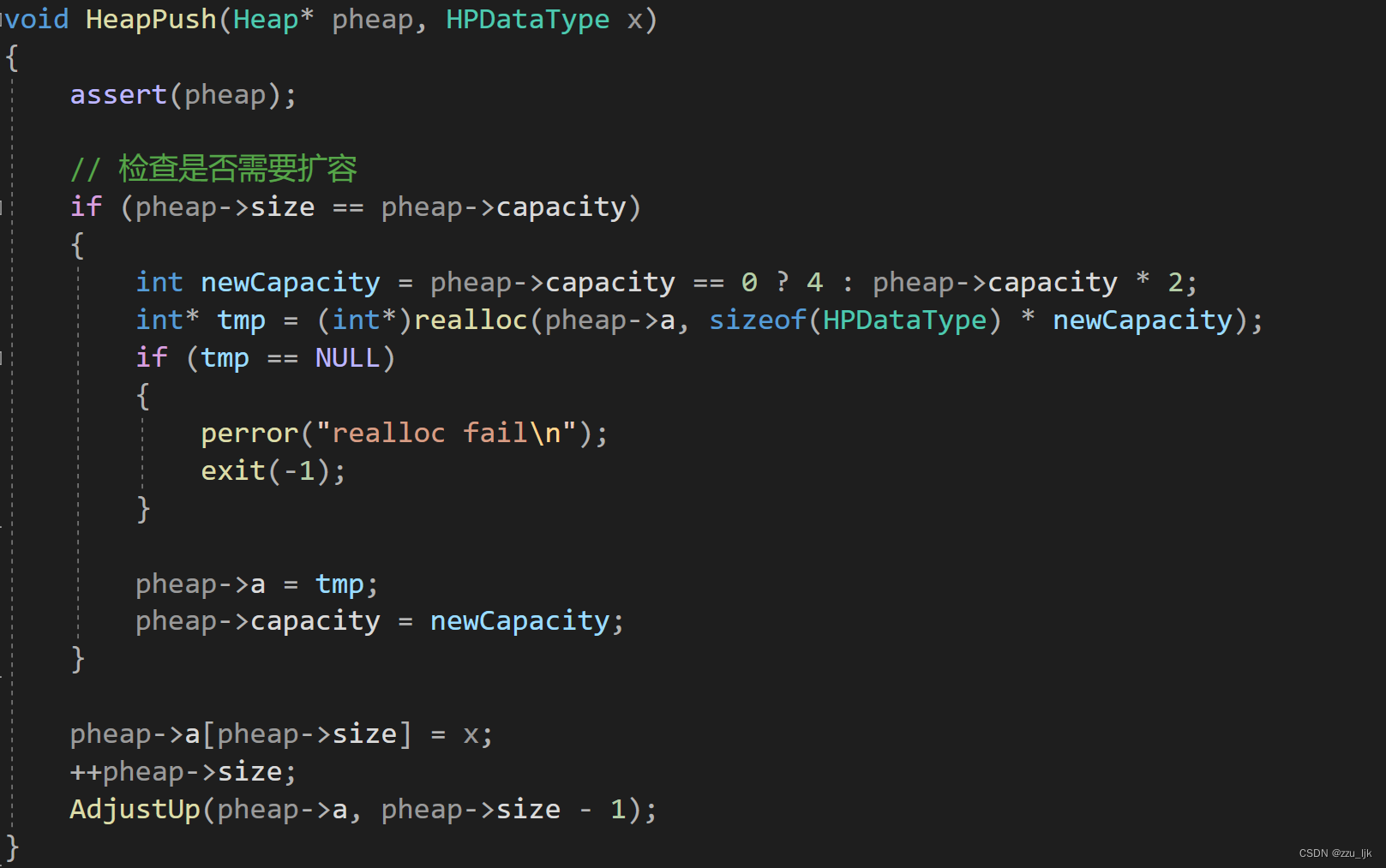
这里使用了向上调整算法

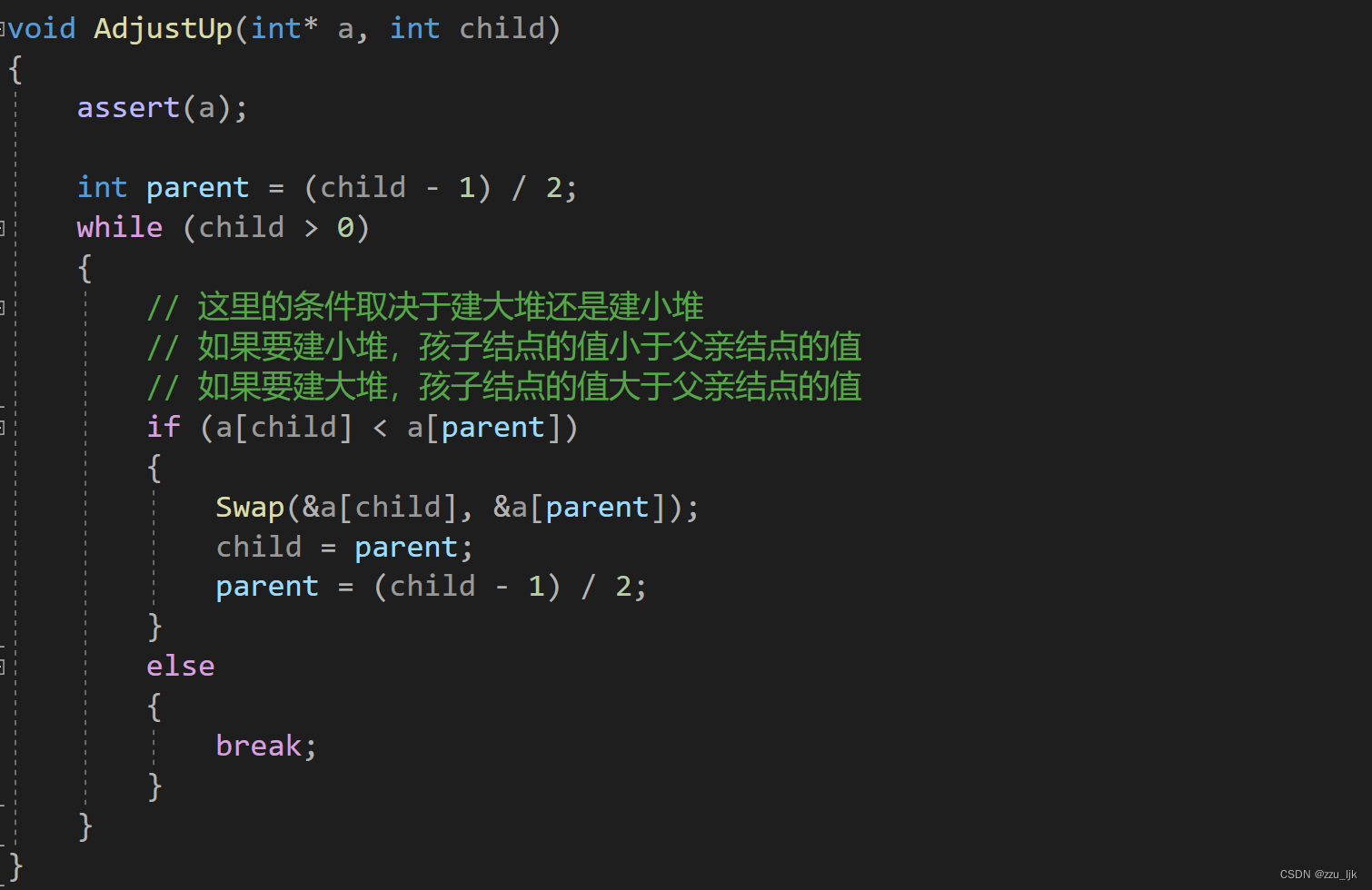
HeapPop

这里使用了向下调整算法

3. 堆的应用

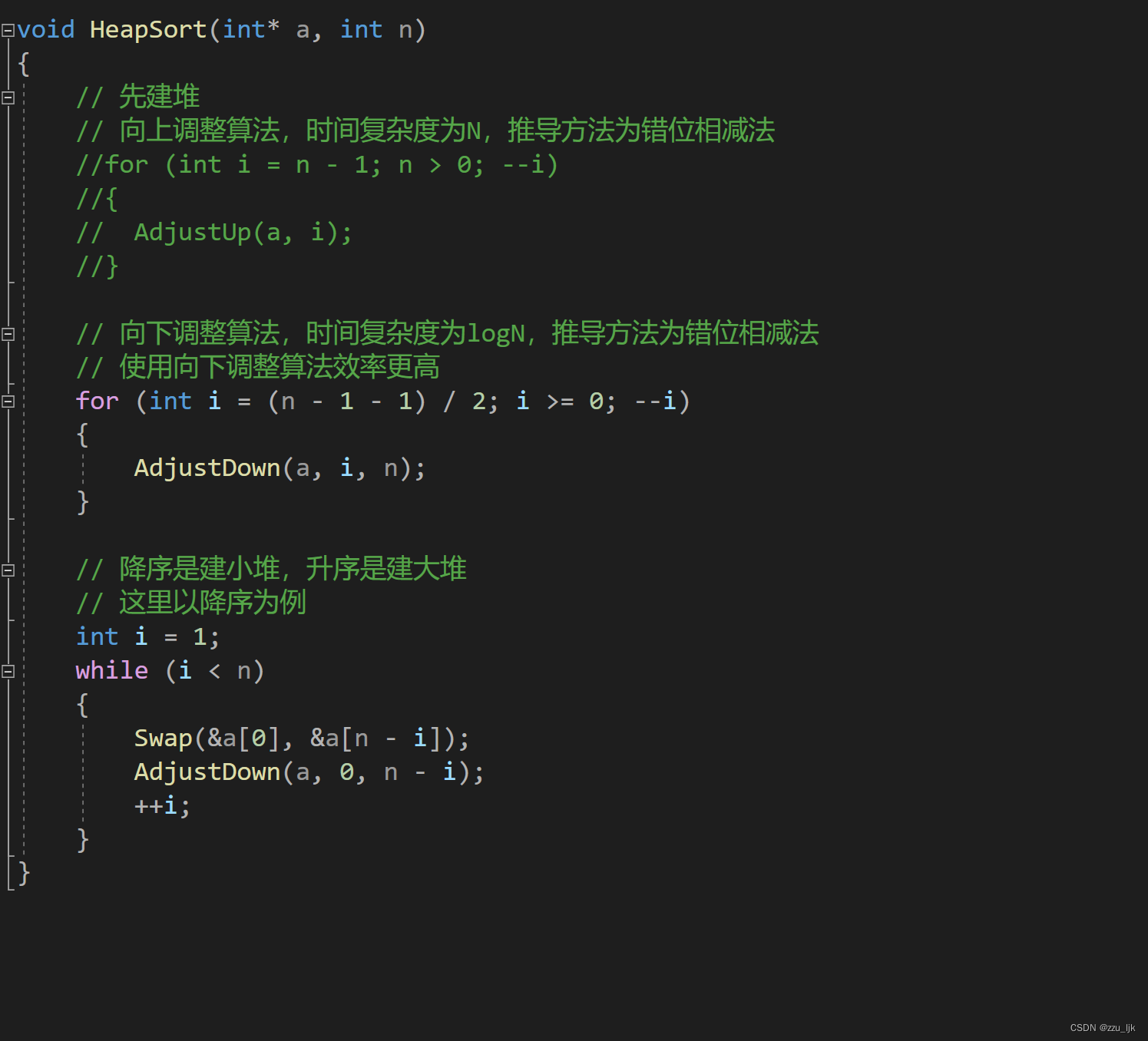
堆排序

升序建大堆，降序建小堆

TopK问题

TopK问题即在N个数中（N非常大）选出前K个最大或者最小的数
这里以选出前K个最大的数为例
选出最大的前K个数可以建大堆也可以建小堆

如果建大堆，思路就和堆排序的思路一样，都是需要先建堆，然后进行选数即可，不同的是这样选数只需要选K次。时间复杂度为N + logK。但是这个方法有一定的弊端。我们不妨设想，当数据非常大的时候，也就是不能全部放在内存的时候，比如10亿个整数，需要40个G的空间来存储，这个时候这40个G就只能放在磁盘中了。我们建堆的话就只能分批次在磁盘中拿数据，然后分部分地建堆，最后再将每部分最大的数据放在一起。这样的话，效率就减慢了，但是也不能说太慢，也在我们可以接受的范围之内。
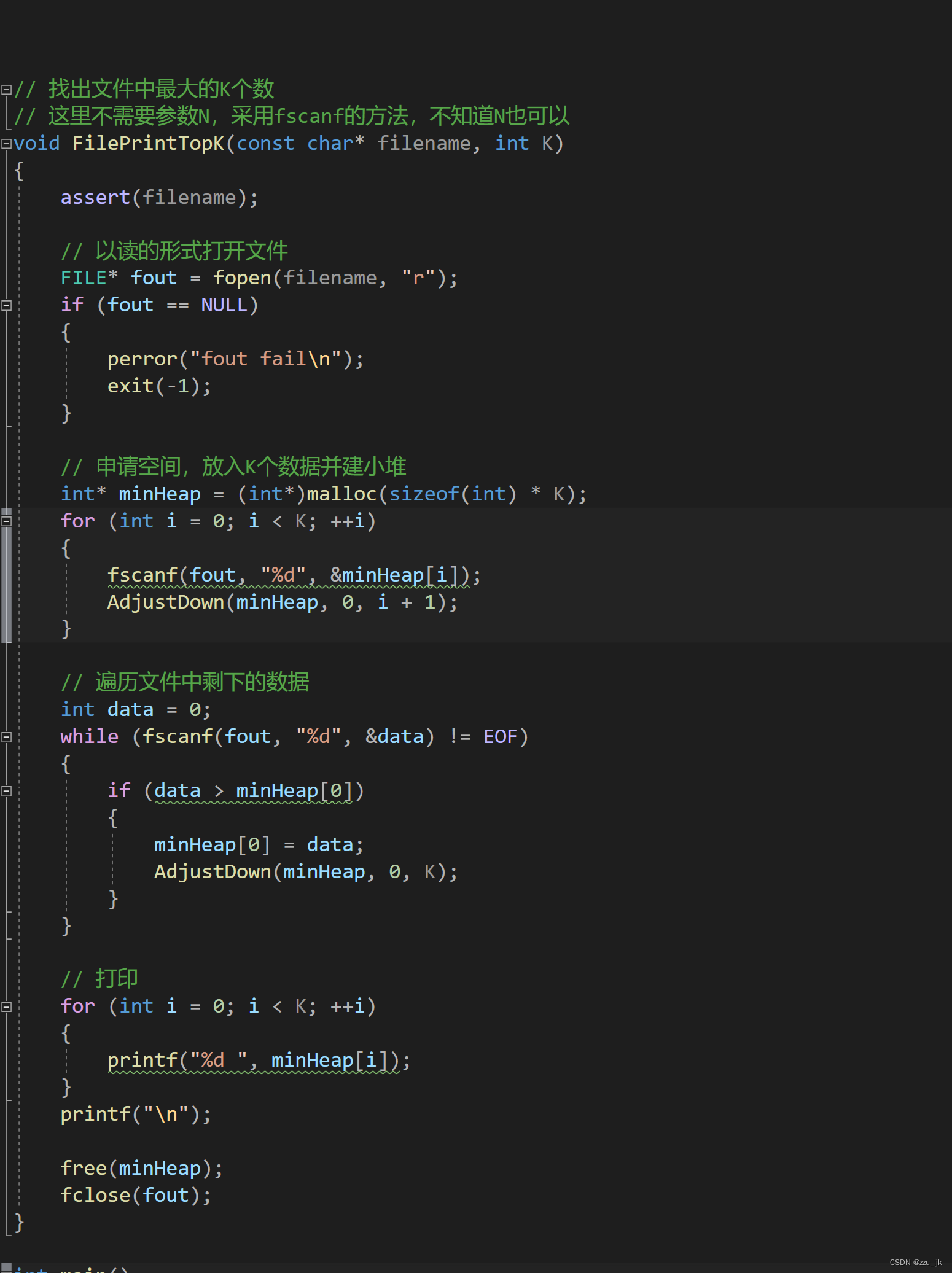
如果建小堆，用小堆来选出最大的K个数，小堆的第一个数是最小的那个数，然后再便利剩下N - K个 数，当有数比小堆中最小的那个数更大时，就将最小的那个数的值赋给堆顶的数，然后使用向下调整算法。时间复杂度为
logK + (N - K)* logK。数据较少时和建大堆的时间复杂度相差不大，但是当数据较大它的优势就很明显了。

结论是选最大K个数建小堆更好，选最小K个数建大堆更好

下面给出选最大K个数建小堆的代码

这里再尝试使用堆来选出磁盘数据中最大的K个数

首先创建文件，并在文件中写入大量的随机数。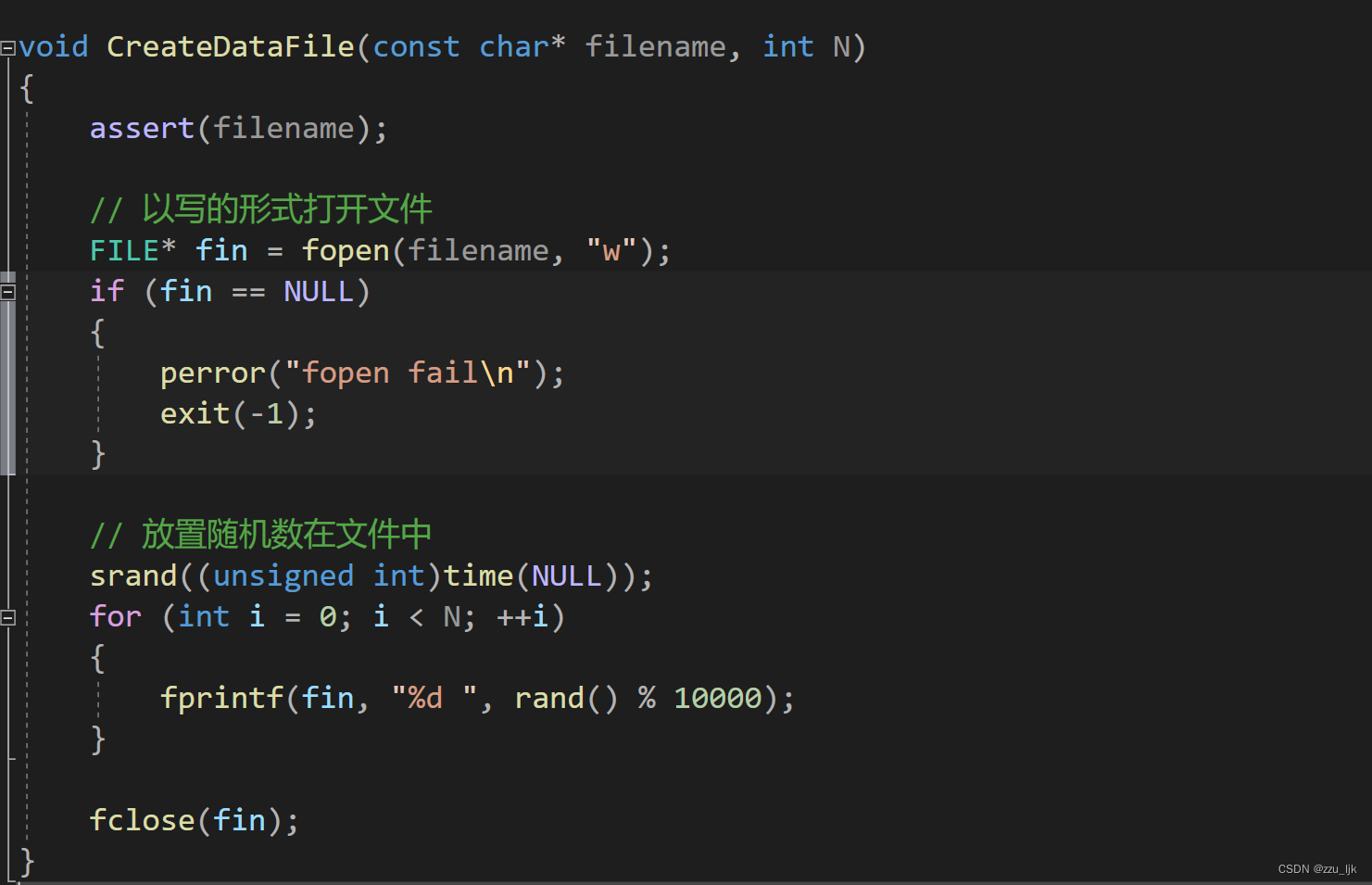
再随便放入几个比更大的数在文件中，这样做的目的是验证我们最终选出的数是否是最大的数。