一、快排

原始快排

算法思想：

ps：排序的效果其实就是使一个数列中的每个数都满足左边数比它小、右边数比它大（假设升序）。

接下来我们来了解快排：

多次递归遍历，每单次遍历，设定一个限定值，单词遍历后，使限定值的左侧值均小于等于限定值，使限定值的右侧值均大于限定值 ，这样就使整体数列中的一个值处在其对应位置上。

之后以上一个限定值为边界，将其左右两侧的子数列分别进行上述单次遍历，最终使得整体数列中的每个值都达到其对应位置上，达到排序的效果。

实现思路：

单次遍历：设定两个指针left 和 right， 每次以数列组的第一个元素为限定值 。left （处于队首）负责找比限定值小的元素，right（处于队尾）负责找比限定值大的元素 。

第一步：left遇到比限定值小（或等于）的元素继续向前遍历（left++），遇到比限定值大的元素就停止遍历，

第二步：当left停止遍历后，right 进行遍历：遇到比限定值大的元素继续向前遍历(right--)，遇到比限定值小（或等于）的元素就停止遍历，然后将left与right所指的值交换 。

第三步:重复上述一二步，直至left与right相遇 ，此时left所指元素小于等于限定值，然后将left所指值与限定值交换 ，至此单次遍历完成，限定值也到达其对应位置 。

多次递归遍历：设定两个变量L和R用来界定单次遍历的范围。(类似二叉树前序遍历)

第一次单次遍历范围(L,R)；左子数列遍历范围：（L，left）;右子数列遍历范围：（left+1，R）

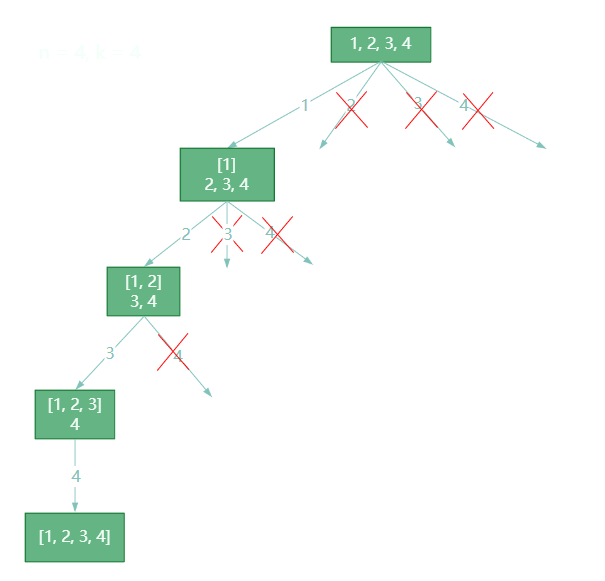
动态图解析：

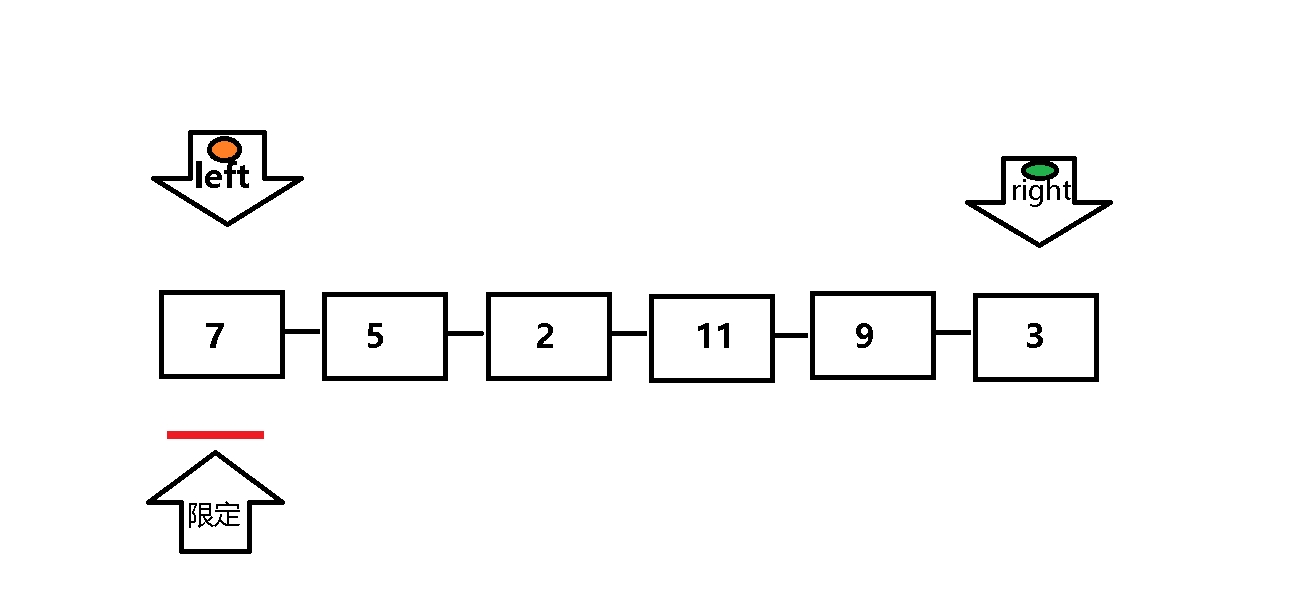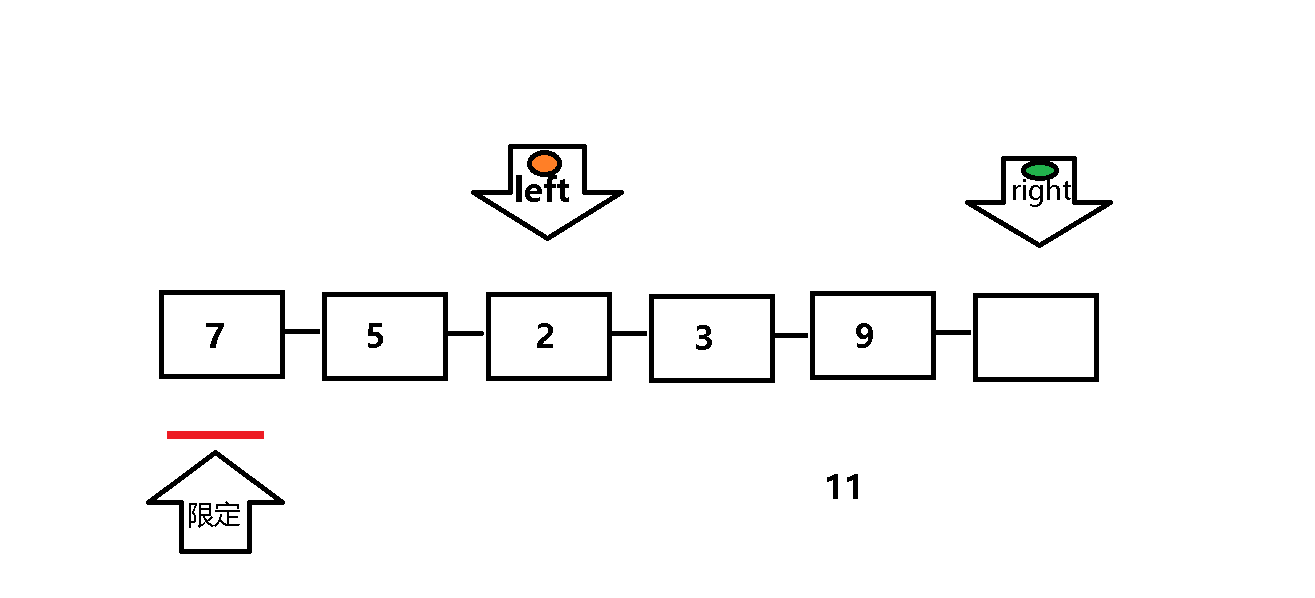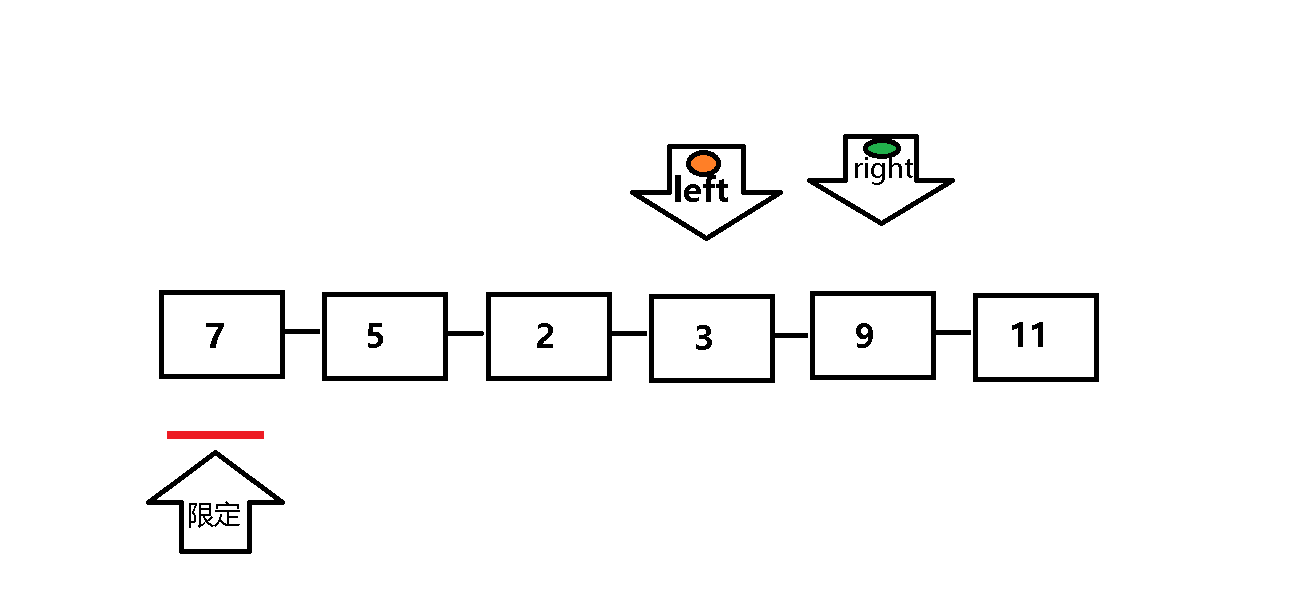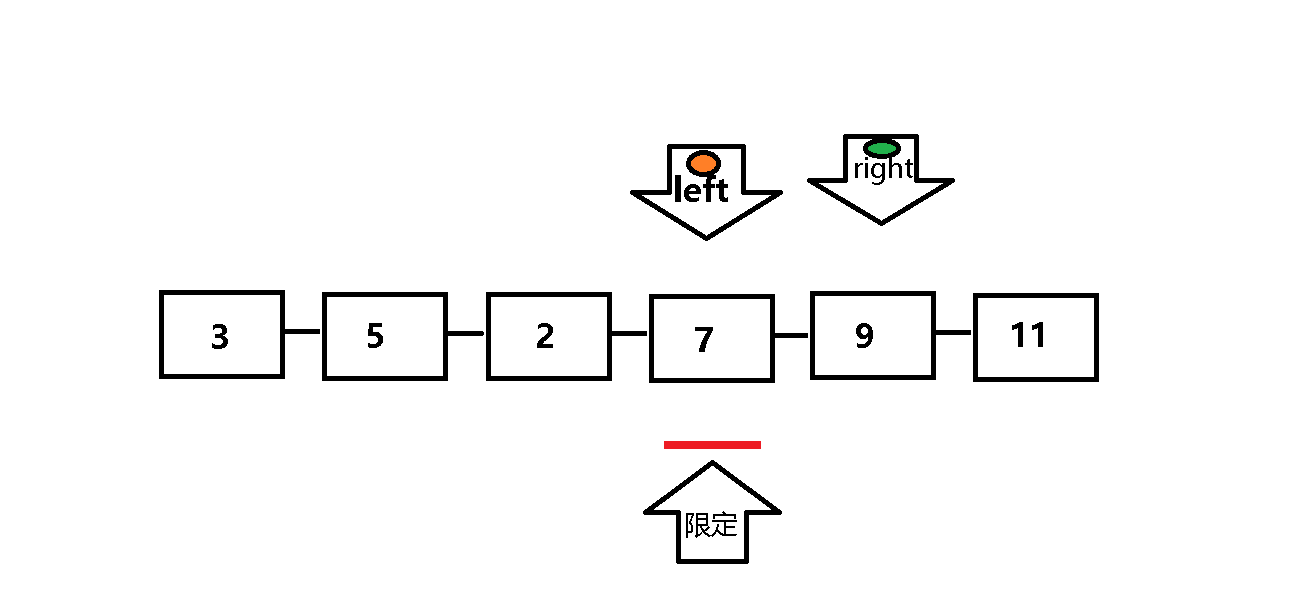
代码实现：

void Qsort(int* pq,int L ,int R)
{
    if (L>=(R-1))
        return;
    int base = L;               //初始限定值为数列的首元素
    int left = L,right = R-1;
    for (; left < right;)
    {       //左侧先遍历保证最后left指向值小于等于限定值
        for (; left!= right&&pq[left + 1] <= pq[base];)    //注意防止越界
        {
            left++;
        }
        for (; right!=left&&pq[right] > pq[base];)         //注意防止越界
        {
            right--;
        }
        if(right!=left)
        swap(&pq[left + 1], &pq[right]);
    }
    swap(&pq[left], &pq[base]);

    Qsort(pq,L, left);                   //遍历左侧子数列
    Qsort(pq,left+1,R);                  //遍历右侧子数列
    
}

挖坑法快排

算法思想:

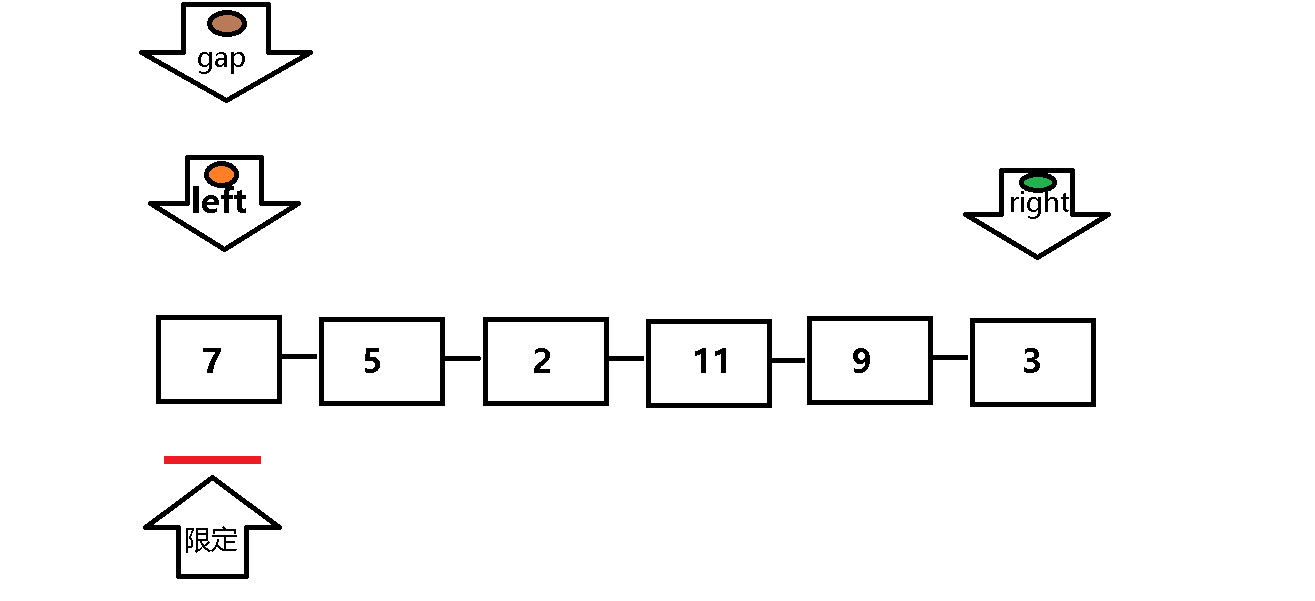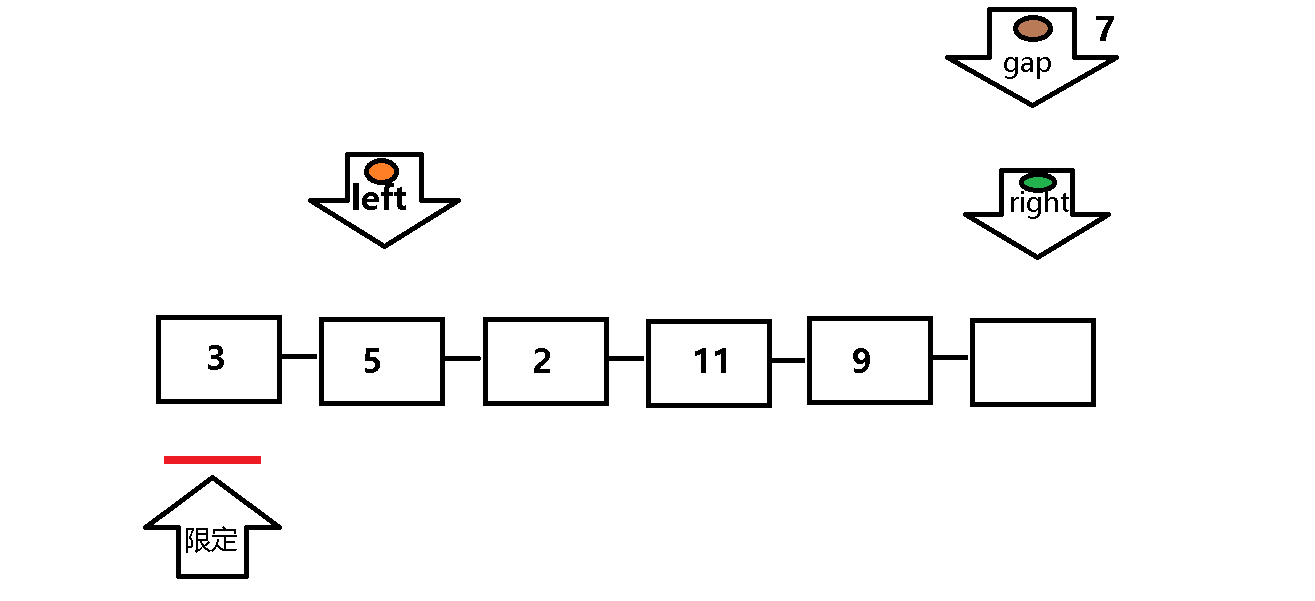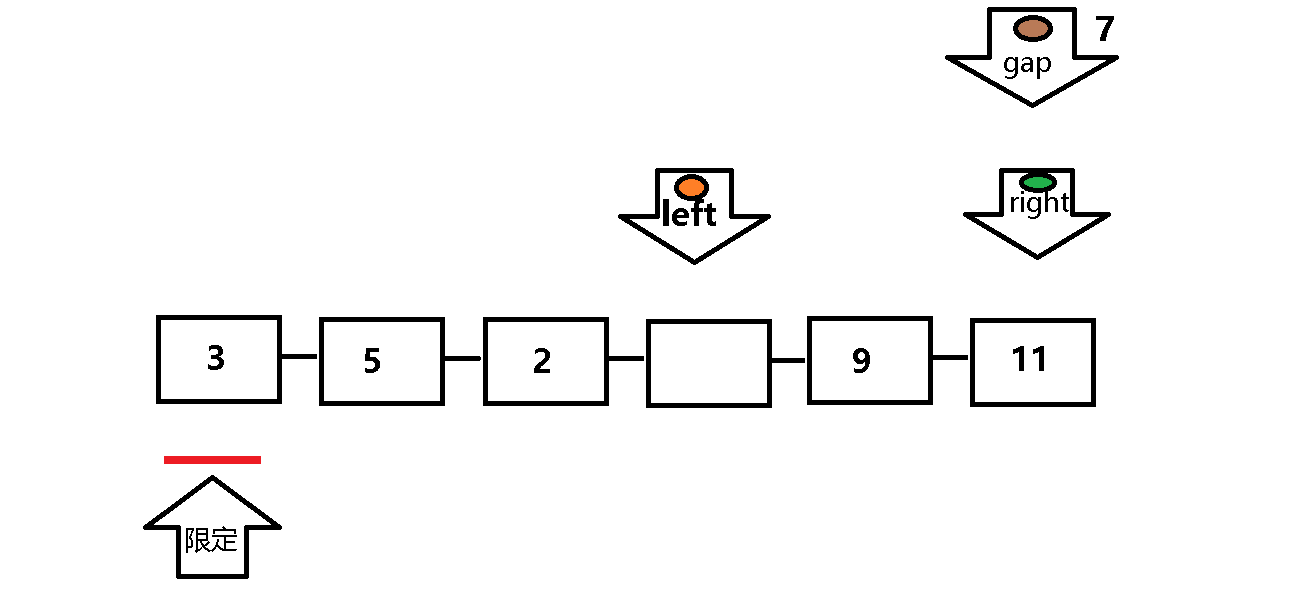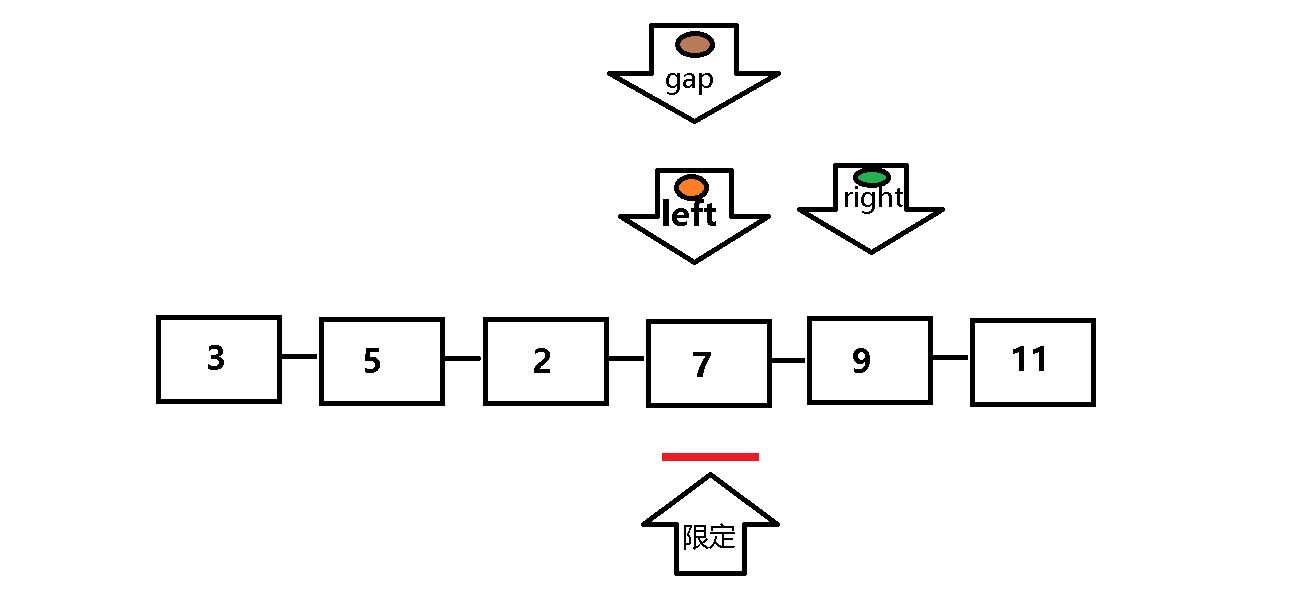
挖坑法与原始快排的遍历顺序基本相同，但是挖坑法的逻辑思维相对更加直接 。

起始用gap记录限定值（gap即为坑），right先走遇到大于限定值继续遍历，遇到小于等于限定值的元素，将其放入坑中（gap）,然后将right的位置记为坑，left重复right的遍历过程。

实现思路：

放入坑中（gap = right 或 gap = left ) 。其余基本和原始快排相同 。

动态图解析：

代码实现：

void GapQsort(int* pq, int L, int R)
{
    if (L >= (R))
        return;
    int gap = L;
    int left = L, right = R - 1;
    int base = pq[L];
    for (; left < right;)
    {
        for (; right!=left&& pq[right] > base; right--);
        pq[gap] = pq[right];
        gap = right;
        for (; left != right && pq[left] <= base; left++);
        pq[gap] = pq[left];
        gap = left;
    }
    pq[gap] = base;
    GapQsort(pq, L, gap);
    GapQsort(pq, gap + 1, R);
}

前后指针法快排

算法思想：

通过两个指针分别以不同的方式遍历数列，形成距离差和标志位，以节约时间复杂度。

快指针负责找大于限定值的元素，慢指针负责找小于等于限定值的元素。

实现思路：

单次遍历：定义前指针front 和后指针 last ，front正常向前遍历，front每遍历一个元素，last做一次检查：last所指元素是否小于等于限定值，若符合，则last也向前遍历；反之，last停止遍历，等待front向前遍历找到小于等于限定值的元素，然后将front与last指定元素交换 ，以此类推，直到front遍历完整个数列，然后将限定值交换至last的位置上 。

动态图解析：

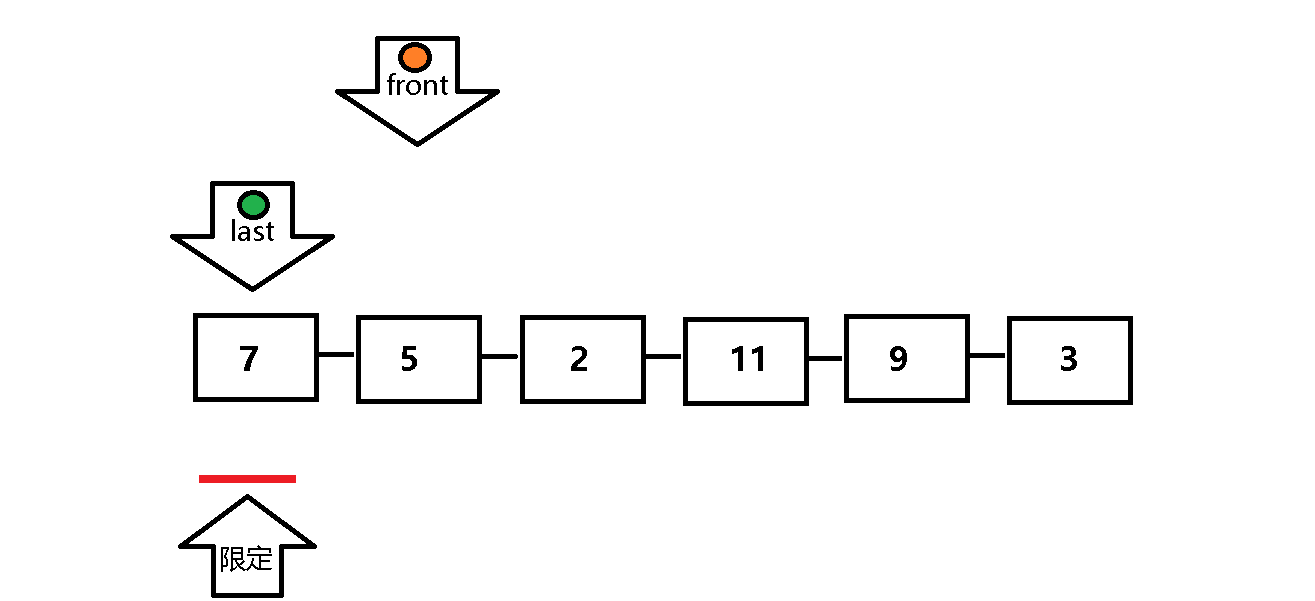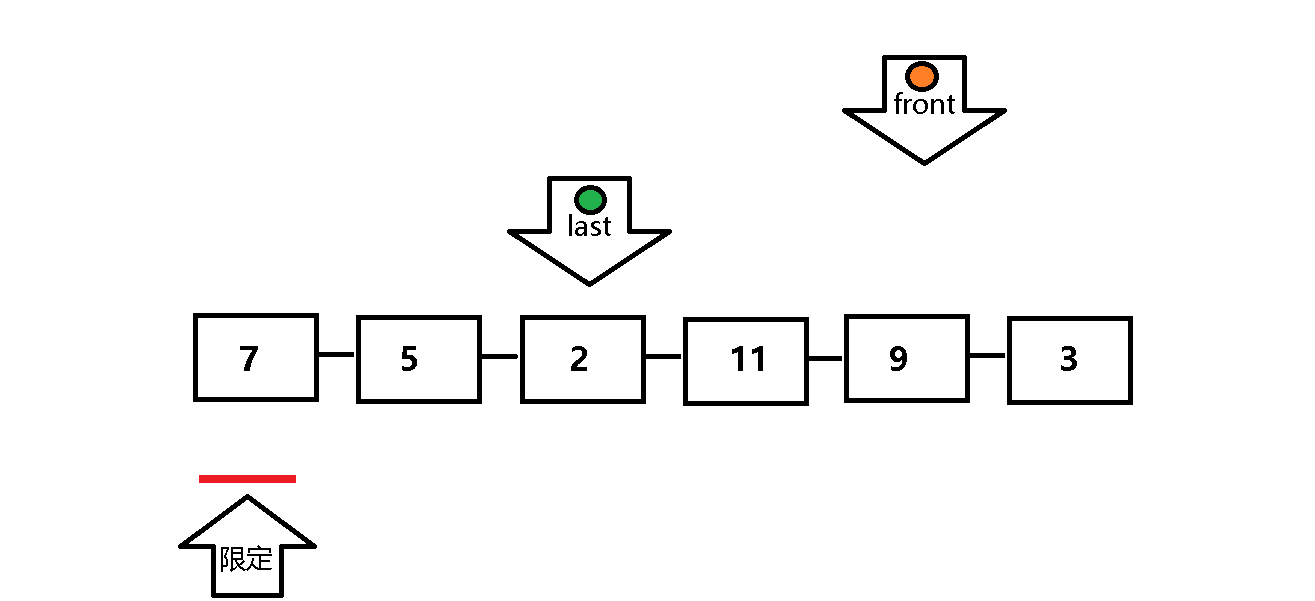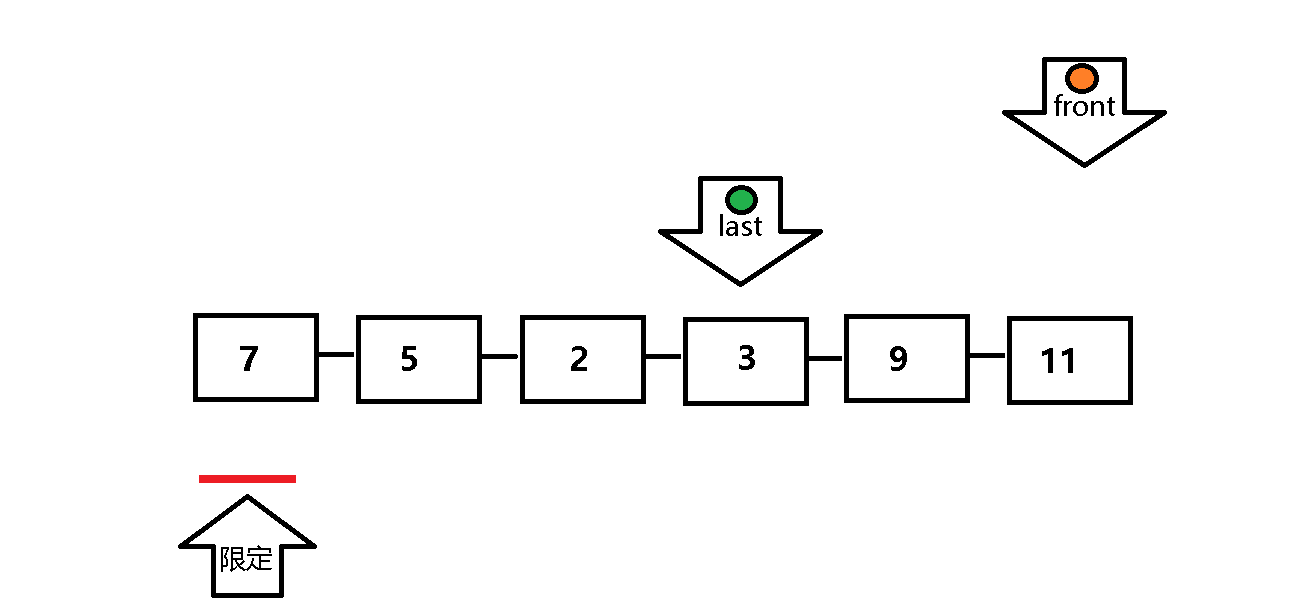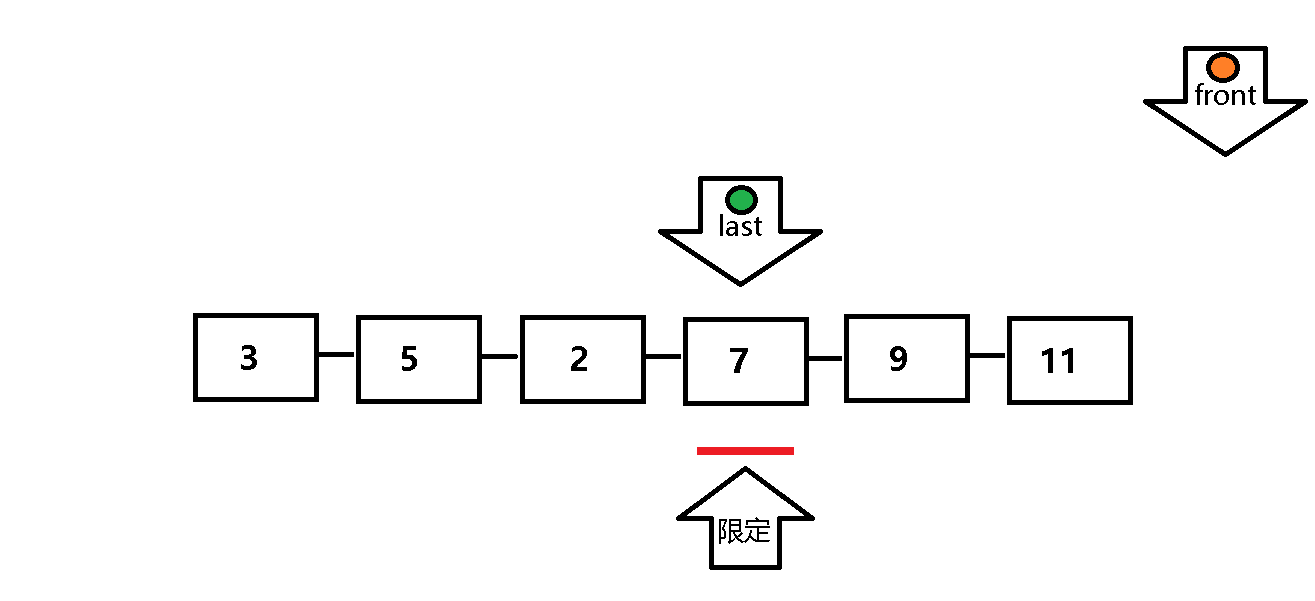
代码实现：

void FRQsort(int* pq, int L, int R)
{
    if (L >= R)
        return;
    int front, last;
    front = last = L;
    int base = Getmid(pq,L,R-1);
    swap(&pq[base], &pq[L]);
    for (front++; front < R; front++)
    {
        if (pq[front] <= pq[L])
            swap(&pq[front], &pq[++last]);
    }
    swap(&pq[last], &pq[L]);
    FRQsort(pq, L, last);
    FRQsort(pq, last+1, R);

}    
int Getmid(int* pq, int left,int right)
{
    int mid = pq[(left+right) / 2];
    if (pq[mid] < pq[left])
    {
        if (pq[left] < pq[right])
            return left;
        else if (pq[mid] < pq[right])
        {
            return right;
        }
        else
            return mid;
    }
    else
    {
        if (pq[right] < pq[left])
            return left;
        else if (pq[mid] < pq[right])
            return mid;
        else
            return right;
    }
}

非递归实现快排

算法思想：

前后指针法多次排序的方式是通过将排序数列的范围作为函数参数来实现的，而非递归的实现中，单次排序的方式与前后指针法无异，区别在于多次排序：将排序数列的范围传入栈空间中，进而达到递归的效果。

例：假设待排序数列的元素如下（以下标形式）： 0 1 2 3 4 5

第一次排序传入排序数列范围 （0，5）， 假设单次排序后限定值下标为 2 ；

第二次排序传入排序数列范围 （0，1），（3，5）假设单次排序后限定值下标分别为 1 ，4

第三次排序传入排序数列范围 （0，0），（3，3），（5，5）

此时传入下标相等，说明只有一个元素，则排序无意义，即无需排序。

实现思路：

第一步将初始数列范围入栈，用一个变量basei表示限定值的下标，用left,right表示范围

第二步在不越界的情况下，将左右子数列分别入栈 。注：遍历子数列时要更新left,right

越界判定：
保持不越界且左子数列至少有两个元素 ：basei >= left + 2
同理，右子数列防越界判定 ：basei <= right - 3

代码实现：

void No_reQSort(int* pq,int k)
{
    Stack* newstack = (int*)malloc(sizeof(Stack));
    Stack_init(newstack);
    Stack_push(newstack, 0);
    Stack_push(newstack, k);

    for (int left, right; Stack_Empty(newstack);)
    {
        right = Stack_Top(newstack);
        Stack_pop(newstack);
        left = Stack_Top(newstack);
        Stack_pop(newstack);
        int basei = auxFRQsort(pq, left, right);
        if (basei >= left + 2)
        {
            Stack_push(newstack, left);
            Stack_push(newstack, basei);
        }
        if (basei <= right - 3)
        {
            Stack_push(newstack, basei + 1);
            Stack_push(newstack, k);
        }
    }
}

二、归并排序

递归实现归并

算法思想：

假设有两个数列a（2，1，3）和b（5，4）将这两个数列组合成一个有固定顺序的（升/降序）数列，这个过程即为两个数列的归并排序。

所以，若有一个待排序数列，我们可以将其分为多个子数列，并对每对子数列进行递归排序，最终使得整体数列有序。

归并排序包含三大部分：两个子数列排序，整体数列分层递归

两个子数列排序：

建立一块新空间（两个子数列合并大小）用两个指针分别遍历两个子数列 ，（假设升序）利用指针比较子数列的元素，元素小的数列将优先拷贝到新空间，直至其中一个子数列先被拷贝完，

再将剩于的一个数列的元素全部拷贝到新空间。

整体数列分层递归：

先将数列按照逐层分裂1/2的方式分解，再从最后一层开始排序并逐层归并。

实现思路：

两个函数的设置，子数列归并排序函数的参数要能表现两个子数列的范围，

整体递归函数的参数要能表示前1/2的数列范围和后1/2的数列范围。

下面代码用的是 （L1，R1） && （L2，R2）

动态解析：

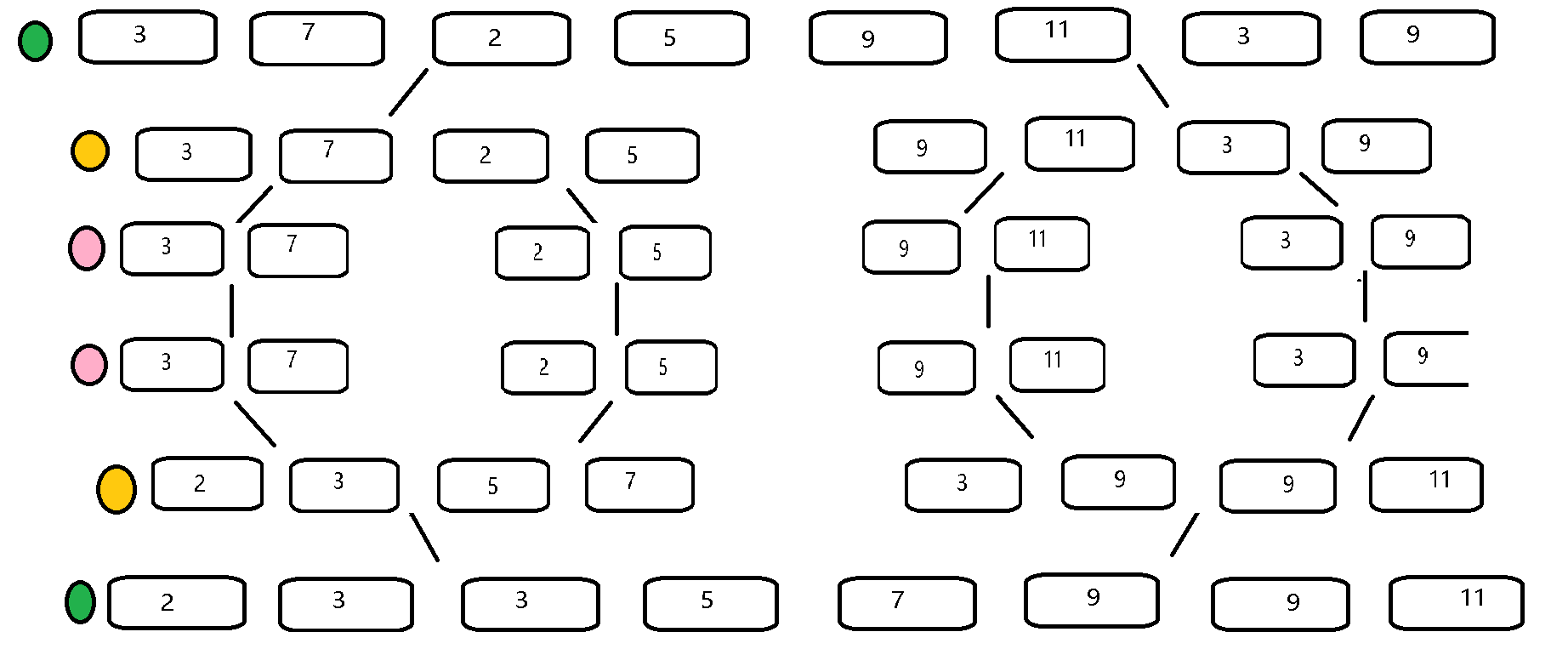
代码实现：

void Tstrcpy(int* a, const int* b,int quant)
{
    for (int i = 0; i < quant; i++)
        a[i] = b[i];
}
void MergeSort(int* pq, int L1, int R1, int L2, int R2)
{
    int L1L = L1, R1R = R1;
    int L2L = L2, R2R = R2;
    int square = R2-L1+1;
    int* temp = (int*)malloc(sizeof(int) * square);
    int i = 0;
    for (i = 0; L1L <= R1R && L2L <= R2R;)
    {
        if (pq[L1L] > pq[L2L])
        {
            temp[i++] = pq[L2L++];
        }
        else
            temp[i++] = pq[L1L++];
    }
    int xtem = (L1L > R1R) ? L2L : L1L;
    for (int k = i; i < square; )
        temp[i++] = pq[xtem++];
    Tstrcpy(&pq[L1], temp, square);
}
void Merge(int *pq,int head,int tail)
{
    if (head >= tail)
        return;
    int L1 = head, R1 = (head + tail) / 2;
    int L2 = (head + tail) / 2 + 1, R2 = tail;
    Merge(pq, L1, R1);
    Merge(pq, L2, R2);
    MergeSort(pq,L1,R1,L2,R2);
}

非递归实现归并

算法思想：

通过下标数值计算的方式，将相邻数列逐次排序。

实现思路：

定义一个gap ,初始为1 ，为相邻子数列的大小 ，每遍历一边gap *= 2，

直至数组以最大二等分的形式进行最后一次归并排序。

其中下标数值的计算可能会出现越界的情况，所以需要针对具体情况进行约束。

代码实现：

void No_reMerge(int* pq, int head, int tail)
{
    int gap = 1;
    int L1, R1, L2, R2 = 0;
    for (; gap <= tail; gap *= 2)
    {
        for (int head = 0,R2 = 0;R2<tail-1;head=head+2*gap)
        {
            L1 = head, R1 = head + gap - 1;
            L2 = head + gap, R2 = head - 1+2*gap;
            if (R1 >= tail)
                R1 = tail-1;
            if (L2 >= tail)
                L2 = tail-1;
            if (R2 >= tail)
                R2 = tail-1;
            //printf("( %d,%d--%d,%d )--", L1, R1, L2, R2);
            MergeSort(pq, L1,R1,L2,R2);

        }
        //printf("\n");
    }
}