一、最长单调序列模型

1、模型母题

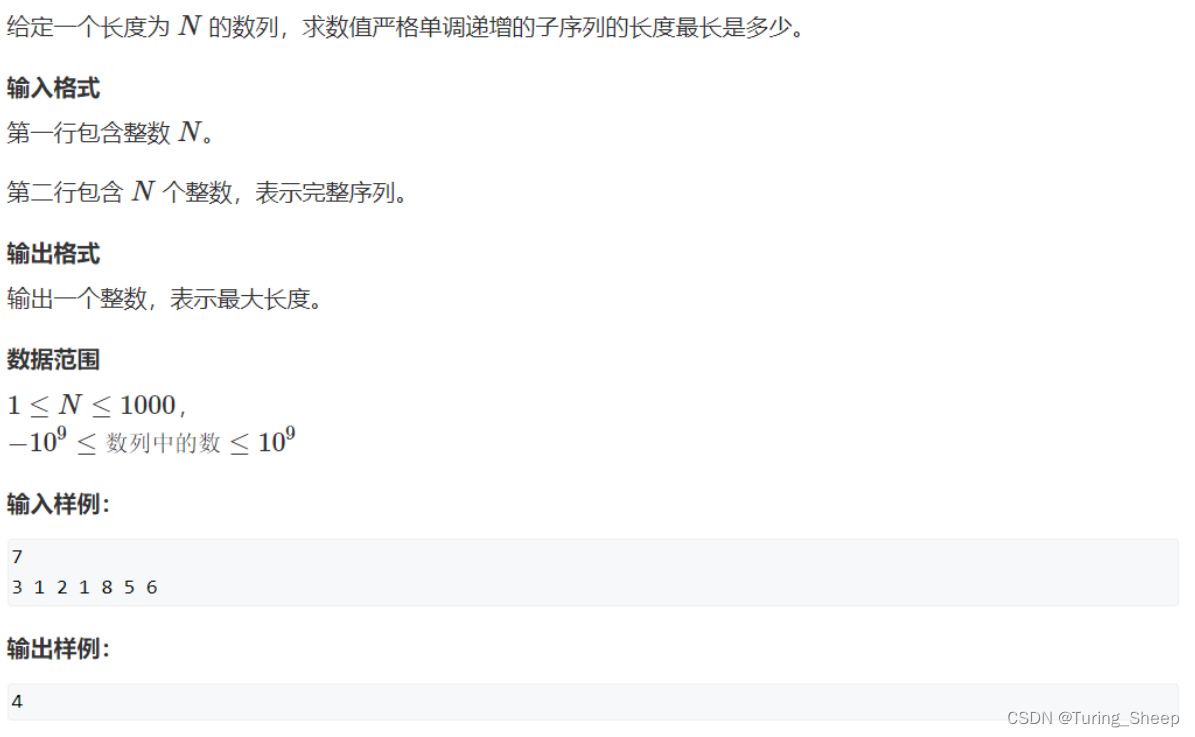
2、思路分析（两种方法：DP，贪心）

这道母题作者在之前的文章中做过详细的解答，如果大家对这两种方法不太理解的话，作者建议先去看之前的文章。最长上升子序列模型

二、模型的应用

1、AcWing 1017. 怪盗基德的滑翔翼

（1）问题

（2）分析

这道题就是一个很单纯的单调序列的使用，大家只需要分别求出最长上升子序列和最长下降子序列，然后比较出一个最大值输出即可。

（3）代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
typedef long long ll;
const int N=110;
int a1[N],a2[N],f1[N],f2[N];
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",a1+i);
        }
        for(int i=n;i>0;i--)a2[i]=a1[n-i+1];
        for(int i=1;i<=n;i++)f1[i]=1,f2[i]=1;
        for(int i=1;i<=n;i++)
        {
            for(int j=i-1;j>0;j--)
            {
                if(a1[i]<a1[j])
                {
                    f1[i]=max(f1[i],f1[j]+1);
                }
            }
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=i-1;j>0;j--)
            {
                if(a2[i]<a2[j])
                {
                    f2[i]=max(f2[i],f2[j]+1);
                }
            }
        }

        int ma=0;
        for(int i=1;i<=n;i++)
        {
            ma=max(f1[i],ma);
        }
        for(int i=1;i<=n;i++)
        {
            ma=max(f2[i],ma);
        }
        cout<<ma<<endl;
        
    }
    return 0;
}

2、AcWing 1014. 登山

（1）问题

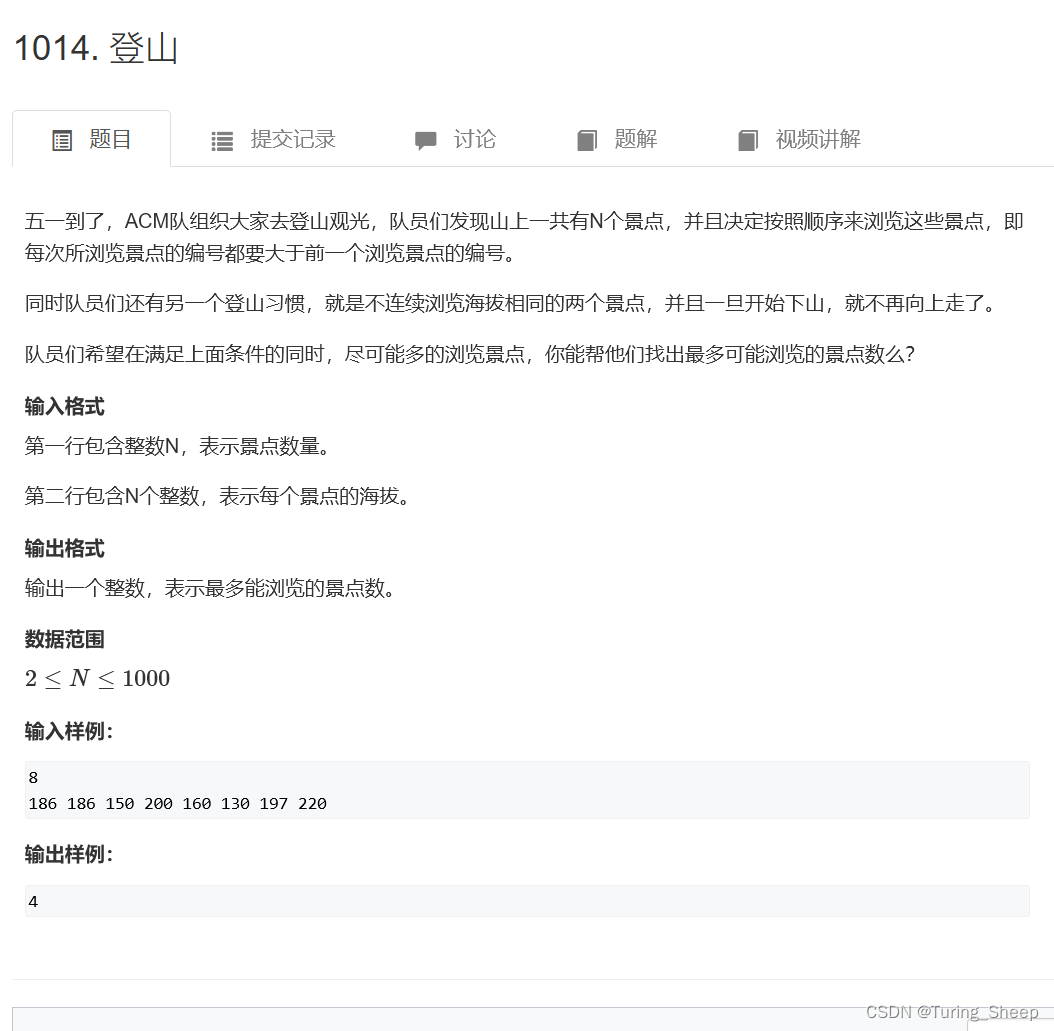
（2）分析

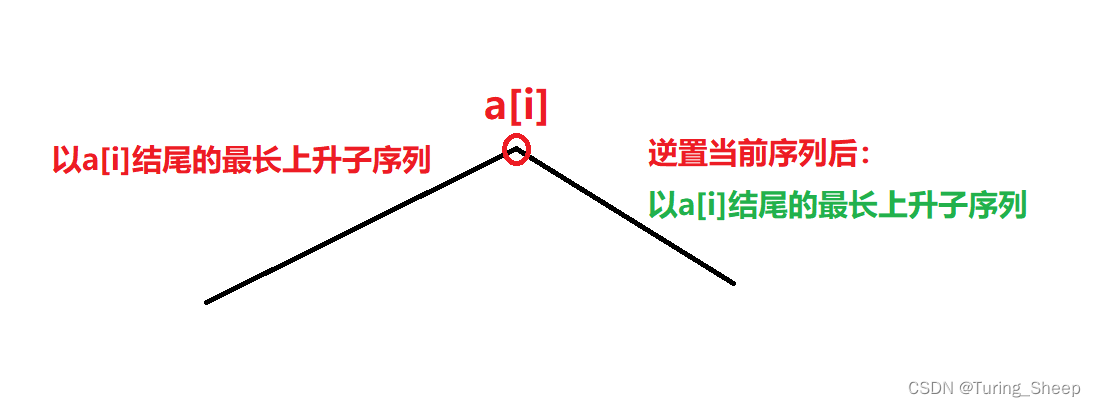
通过上面的图，我们只需要求出以a[i]结尾的正序的最长上升子序列长度l,以及以a[i]为结尾的逆序最长上升子序列的长度m，然后我们找到所有l+m的最大值。

（3）代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e3+10;
int a[N],ra[N];
int f1[N],f2[N],f[N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        scanf("%d",a+i);
    for(int i=n;i>0;i--)
        ra[n-i+1]=a[i];

    for(int i=1;i<=n;i++)f1[i]=1,f2[i]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=i-1;j>0;j--)
        {
            if(a[j]<a[i])
                f1[i]=max(f1[i],f1[j]+1);
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=i-1;j>0;j--)
        {
            if(ra[j]<ra[i])
                f2[i]=max(f2[i],f2[j]+1);
        }
    }
    int ma=0;
    for(int i=1;i<=n;i++)
    {
        f[i]=f1[i]+f2[n-i+1]-1;
        ma=max(f[i],ma);
    }
    cout<<ma<<endl;
    return 0;
}

3、AcWing 482. 合唱队形

（1）问题

（2）分析

这道题和登山的题目几乎一样。

（3）代码

#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int a[N],ra[N];
int f1[N],f2[N],f[N];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)scanf("%d",a+i);
    for(int i=n;i>0;i--)ra[n-i+1]=a[i];
    for(int i=1;i<=n;i++)f1[i]=1,f2[i]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=i-1;j>0;j--)
        {
            if(a[j]<a[i])
                f1[i]=max(f1[i],f1[j]+1);
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=i-1;j>0;j--)
        {
            if(ra[j]<ra[i])
                f2[i]=max(f2[i],f2[j]+1);
        }
    }
    int ma=0;
    for(int i=1;i<=n;i++)
    {
        f[i]=f1[i]+f2[n-i+1]-1;
        ma=max(ma,f[i]);
    }
    cout<<n-ma<<endl;
    return 0;
}

4、AcWing 1012. 友好城市

（1）问题

（2）分析

这道题也是单调序列的变形，但是这道题比之前的两道题不容易看出背后的模型，这道题作者之前已经做过详细地讲解，建议不会的读者去看一下：
传送门：
AcWing 1012. 友好城市

（3）代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef pair<int ,int> pii;
const int N=5100;
pii a[N];
int f[N];
int n;
bool cmp(pii a,pii b)
{
    return a.first<b.first;
}
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)scanf("%d%d",&a[i].first,&a[i].second);
    sort(a,a+n,cmp);
    for(int i=0;i<n;i++)f[i]=1;
    for(int i=0;i<n;i++)
        for(int j=0;j<i;j++)
            if(a[j].second<a[i].second)
                f[i]=max(f[i],f[j]+1);
    int ma=0;
    for(int i=0;i<n;i++)
    {
        ma=max(ma,f[i]);
    }
    cout<<ma<<endl;
    return 0;
}

5、AcWing 1016. 最大上升子序列和

（1）问题

（2）分析

这道题就很简单了，只是从长度变成了最大值，只需要稍作调整即可。将转移方程中的f[j]+1变成f[j]+a[i]。然后初始化的时候初始化为数值本身，而不是1。

（3）代码

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1e3+10;
int a[N],f[N];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)scanf("%d",a+i);
    for(int i=1;i<=n;i++)f[i]=a[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=i-1;j>0;j--)
        {
            if(a[i]>a[j])
            {
                f[i]=max(f[i],f[j]+a[i]);
            }
        }
    }
    int ma=0;
    for(int i=1;i<=n;i++)
    {
        ma=max(f[i],ma);
    }
    cout<<ma<<endl;
    return 0;
}

6、AcWing 1010. 拦截导弹

（1）问题

（2）分析

这道题涉及到了最长上升子序列的贪心做法，在之前的文章中曾经做过详细地讲解，建议读者去看一看那一篇讲解。AcWing 1010. 拦截导弹

（3）代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e6+10;
int a[N],f[N],g[N];
int n;
int main()
{
    while(cin>>a[n])n++;
    int len1=0;
    for(int i=0;i<n;i++)
    {
        int l=0,r=len1;
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(f[mid]>=a[i])l=mid;
            else r=mid-1;
        }
        len1=max(len1,r+1);
        f[r+1]=a[i];
    }
    cout<<len1<<endl;
    int len2=0;
    for(int i=0;i<n;i++)
    {
        int l=0,r=len2;
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(g[mid]<a[i])l=mid;
            else r=mid-1;
        }
        len2=max(len2,r+1);
        g[r+1]=a[i];
    }
    cout<<len2<<endl;
    return 0;
}