POJ3263. Tallest Cow

传送门：Tallest Cow

---

题目：

有N头牛站成一行。两头作能够相支看见，当且仅当它们中间的牛身高都比它们矮。现在，我们只知道其中最高的牛是第P头，它的身高是H，不知道剩余N-1头牛的身高。但是，我们还她道对关系，每对关系都指明了某两头牛A;和B;可以相互看见。求每头牛的身高最大可能是多少。1≤ N,M ≤ 10*，1≤H≤10。

N：牛的总数，P：身高最高的牛，H：身高最高的牛的身高，M：关系的对数

我们定义一个C数组，初始全部元素为0。

假设告诉了我们 i 与 j 的关系（1<=i<j<=N），因此我们可以知道，在i与j之间的全部位置，即 开区间（i，j）之间的所有的牛的身高都至少比 i和j 矮1，因此，我们可以在每组输入的时候（i，j），对i+1和j-1之间全部的元素都减去1，即C[i+1]-=1…C[j-1]-=1，因为中间位置的牛的身高一定且至少比两边的牛的身高矮1。

再加上 p牛的身高一定是最高的，并且我们已知这个H，所以 C[p]一定等于零，因为从上面的分析可得，我们的C数组表示的是一个变化量，因此对于每一对（i，j）之间的元素，C[x]（i<x<j）都执行减1操作，则最后利用 H+C[x] 就可以得到每一头牛的至少的最高高度。

我们如果对于i，j中的每一个元素都进行-1，则这一定是一个二重循环，时间复杂度达到了O（nm），因此这个算法并不算优秀，但是它的确是可以做出来的。

---

前缀和思想

我们有必要对（i，j）中的每一个 元素都执行 -1的操作吗？？

• 我们只需要对C[i+1]-=1， C[j]+=1 ，就可以了。

为什么呢？我们现在只需要对两个位置的元素进行操作，如果真的可以的话，这个算法将会将到O（n+m）的复杂度，基本适用于所有的竞赛测试。

1. 建立一个数组D，来表示这两个位置的操作：C[i+1]-=1， C[j]+=1，这句话表示的含义是：“身高减少状态从i+1开始，一直延续到 j-1，到 j 结束，所以我们可以把这一段看作一个状态，根据这个状态，我们就可以用前缀和求出这些位置的值，C就等于D的前缀和。
2. 前缀和公式：C[i]=C[i-1]+D[i]
   

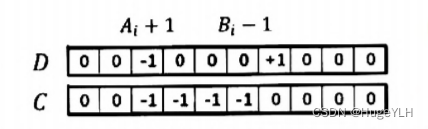
意义：把一段区间的操作转换为对左右两个端点的操作，再通过前缀和逆推出原状态。

代码示例

#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <set>
using namespace std;
int n,p,h,m;
int presum[10005],res[10005];
set<pair<int,int>> s;
int main()
{
    cin>>n>>p>>h>>m; //第p头牛的身高最高
    for (int i=1;i<=m;i++)
    {
        int a,b;
        cin>>a>>b;
        //a始终表示的是左端点，b始终是右端点
        if (a>b) swap(a,b);
        auto p=make_pair(a,b);
        //这一条记录已经被记录了
        if (s.count(p)) continue;
        //对区间左右端点操作
        presum[a+1]-=1;
        presum[b]+=1;
        //加入set，便于去重
        s.insert(p);
    }
    for (int i=1;i<=n;i++)
    {
        //前缀和逆推原状态
        res[i]=res[i-1]+presum[i];
        printf("%d ",h+res[i]);
    }
	return 0;
}