回溯算法理论基础

什么是回溯法

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。回溯是递归的副产品，只要有递归就会有回溯。所以以下讲解中，回溯函数也就是递归函数，指的都是一个函数。

回溯法的效率

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，所以效率并不高。

回溯法解决的问题

组合问题：N 个数里面按一定规则找出 k 个数的集合;
切割问题：一个字符串按一定规则有几种切割方式;
子集问题：一个 N 个数的集合里有多少符合条件的子集;
排列问题：N 个数按一定规则全排列，有几种排列方式;
棋盘问题：N 皇后，解数独等等;

如何理解回溯法

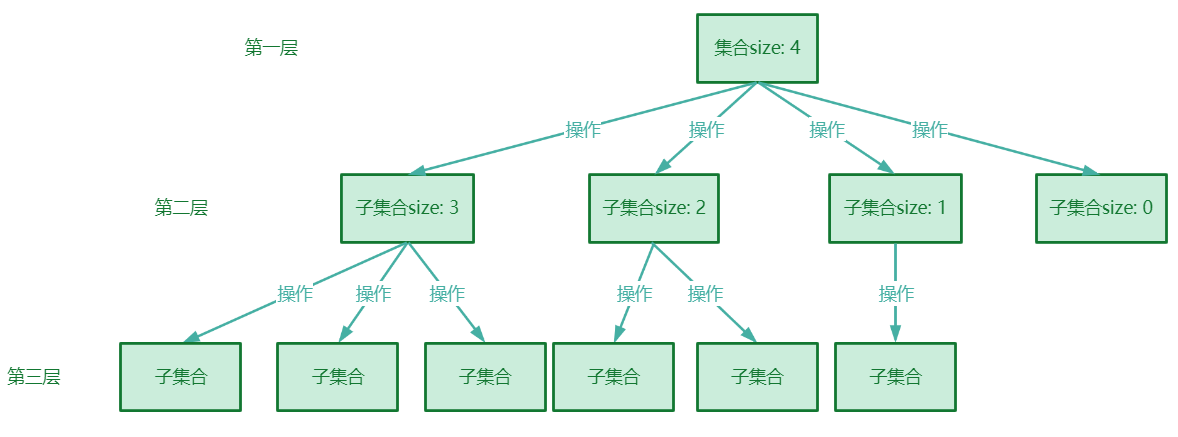
回溯法解决的问题都可以抽象为树形结构，集合的大小构成了树的宽度，递归的深度构成了树的深度。递归会有终止条件，所以一定是一棵高度有限的 N 叉树。

回溯法模板

回溯三步曲
① 回溯函数参数及返回值:
先写逻辑，需要什么参数再填什么参数。一般没有返回值。

void backtracking(参数)

② 回溯函数终止条件:
一般来说搜到叶子结点了也就找到了满足条件的一条答案， 把这条答案存起来，并结束本层递归。

if (终止条件) {
    存放结果;
    return;
}

③ 回溯函数的遍历过程
回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成了树的深度。

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for 循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个 for 循环就执行多少。backtracking 自己调用自己，实现递归。
从图中看出 for 循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。
④ 分析完过程，回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合问题

题目链接：77. 组合
原文链接：77. 组合
视频链接：77. 组合
树形结构：

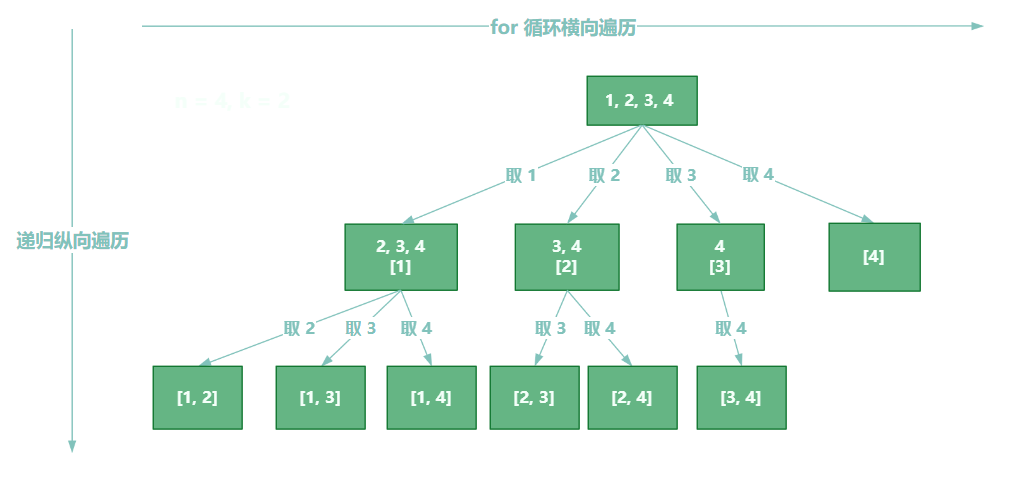
回溯三部曲：
① 确定递归函数参数及返回值：
两个全局变量：

vector<int> path; 			// 用来存放符合条件结果
vector<vector<int>> res;    // 存放符合条件结果的集合

参数除了 $n$ 和 $k$, 还需要有一个 $startIndex$，这个参数用来记录本层递归中集合从哪里开始遍历:

vector<int> path; 			// 用来存放符合条件结果
vector<vector<int>> res;   // 存放符合条件结果的集合
void backtracking(int n, int k, int startIndex) 

② 确定终止条件
path 这个数组的大小如果达到 $k$，说明我们找到了一个子集大小为 $k$ 的组合了，在图中 path 存的就是根节点到叶子节点的路径。

        if (path.size() == k) {
            res.push_back(path);
            return;
        }

③ 确定单层递归逻辑
回溯法的搜索过程就是一个树型结构的遍历过程，在下图中，可以看出 for 循环用来横向遍历，递归的过程是纵向遍历。

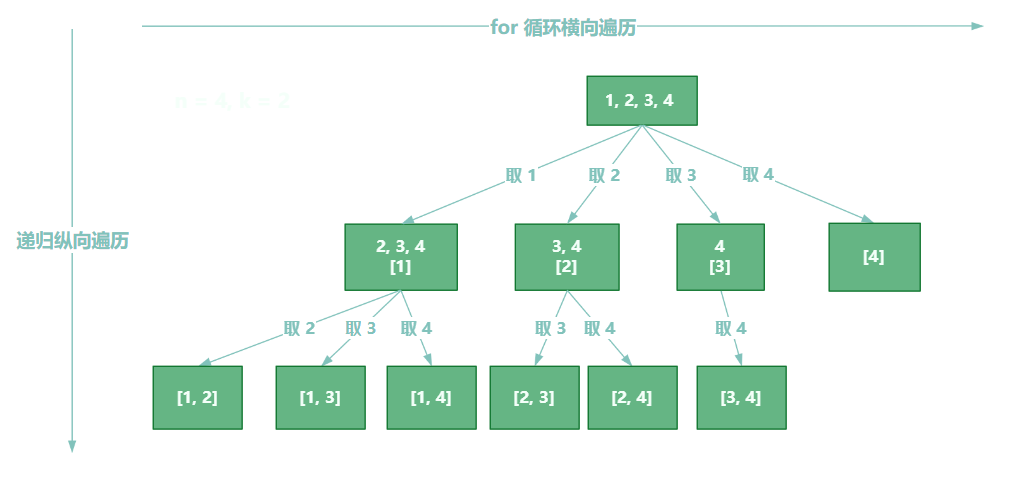
for 循环每次从 $startIndex$ 开始遍历，然后用 $path$ 保存取到的节点 $i$。
backtracking（递归函数）通过不断调用自己一直往深处遍历，总会遇到叶子节点，遇到了叶子节点就要返回。注意下一层搜索要从 $i+1$ 开始。
backtracking 的下面部分就是回溯的操作了，撤销本次处理的结果。

for (int i = startIndex; i <= n; i++) { // 控制树的横向遍历
    path.push_back(i); 					// 处理节点 
    backtracking(n, k, i + 1); 			// 递归：控制树的纵向遍历，注意下一层搜索要从 i+1 开始
    path.pop_back(); 					// 回溯，撤销处理的节点
}

代码如下：

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            res.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i);
            backtracking(n, k, i + 1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return res;
    }
};

组合问题的剪枝优化

视频链接：组合问题的剪枝操作

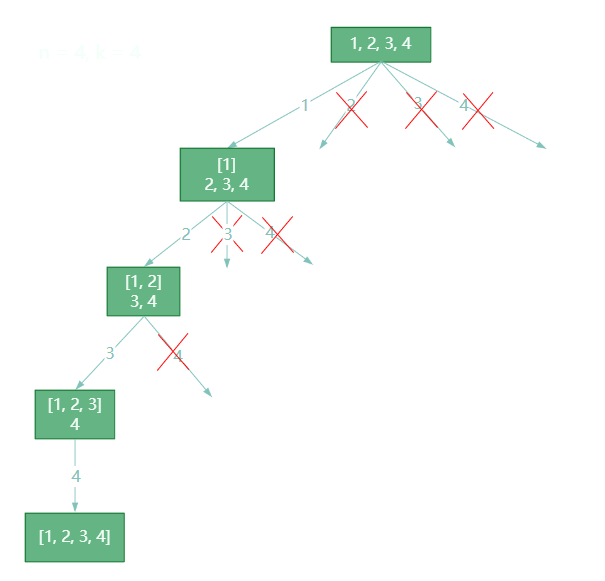
举一个例子，$n=4$，$k=4$ 的话，那么第一层 $for$ 循环的时候，从元素 $2$ 开始的遍历都没有意义了。 在第二层 $for$ 循环，从元素 $3$ 开始的遍历都没有意义了。
图中每一个节点（图中为矩形），就代表本层的一个 $for$ 循环，那么每一层的 $for$ 循环从第二个数开始遍历的话，都没有意义，都是无效遍历。
所以，可以剪枝的地方就在递归中每一层的 $for$ 循环所选择的起始位置。
如果 $for$ 循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了，那么就没有必要搜索了。
优化过程如下：
(1) 已经选择的元素个数：path.size();
(2) 还需要的元素个数为: k - path.size();
(3) 列表中剩余元素（n - i） >= 还需要的元素个数（k - path.size()）;
(4) 在集合 n 中至多要从该起始位置 : i <= n - (k - path.size()) + 1; 开始遍历;
所以优化之后的 for 循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

优化后整体代码：

class Solution {
private:
    vector<int> path;
    vector<vector<int>> res;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            res.push_back(path);
            return ;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) {
            path.push_back(i);
            backtracking(n, k, i + 1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return res;
    }
};