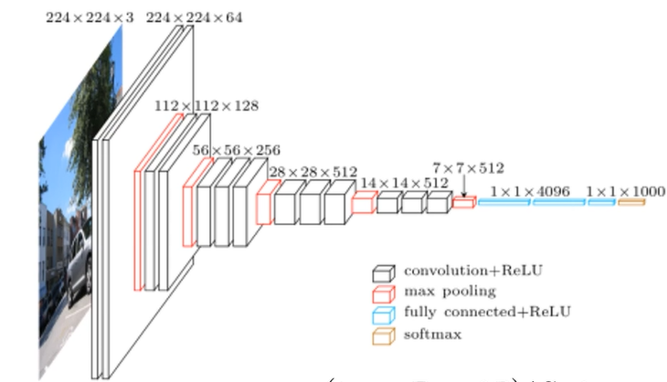
积水面积

先祝大家新年快乐，新的一年，万事如意。

题目描述

一组正整数，分别表示由正方体叠起的柱子的高度。若某高度值为 $x$，表示由 $x$ 个正立方的方块叠起（如下图，$0\le x\le 5000$）。找出所有可能积水的地方（图中蓝色部分），统计它们可能积水的面积总和（计算的是图中的横截面积。一个立方体的位置，为一个单位面积）。

如图：柱子高度变化为 0 1 0 2 1 2 0 0 2 0。

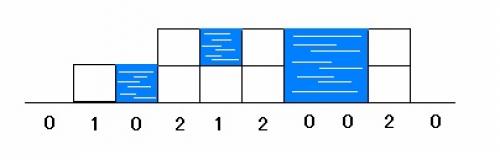
图中蓝色部分为积水面积，共有 $6$ 个单位面积积水。

输入格式

两行，第一行 $n$，表示有 $n$ 个数（$3\le n\le 10000$）。第 $2$ 行连续 $n$ 个数表示依次由正方体叠起的高度，保证首尾为 $0$。

输出格式

一个数，可能积水的面积。

样例 #1

样例输入 #1

10
0 1 0 2 1 2 0 0 2 0

样例输出 #1

6

思路

接雨水，今天偶然看到，又再使用单调栈写了一遍加深印象。

代码实现

import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int ans = 0;
        Deque<Integer> stack = new LinkedList<>();
        int len = sc.nextInt();
        int[] arr = new int[len];
        for(int i = 0; i < len; i++) arr[i] = sc.nextInt();
        for(int i = 0; i < len; i++){
            int cur = arr[i];
            while(!stack.isEmpty() && cur >= arr[stack.peekLast()]){
                int bottom = stack.removeLast();
                if(stack.isEmpty()) break;
                int left = stack.peekLast();
                ans += (Math.min(arr[left], cur) - arr[bottom]) * (i - left - 1);
            }
            stack.addLast(i);
        }
        System.out.println(ans);
        sc.close();
    }
}

最大正方形

题目描述

在一个 $n\times m$ 的只包含 $0$ 和 $1$ 的矩阵里找出一个不包含 $0$ 的最大正方形，输出边长。

输入格式

输入文件第一行为两个整数 $n,m(1\le n,m\le 100)$，接下来 $n$ 行，每行 $m$ 个数字，用空格隔开，$0$ 或 $1$。

输出格式

一个整数，最大正方形的边长。

样例 #1

样例输入 #1

4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1

样例输出 #1

2

思路

可使用动态规划，dp[i][j]的含义为以matrix[i][j] 为右下节点的最大正方形；
状态转移即为：dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1;

代码实现

import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(), m = sc.nextInt();
        int ans = 0;
        int[][] dp = new int[n+1][m+1];
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                int cur = sc.nextInt();
                if(cur != 0){
                    dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1;
                    ans = Math.max(ans, dp[i][j]);
                }
            }
        }
        System.out.println(ans);
        sc.close();
    }
}