一、问题描述

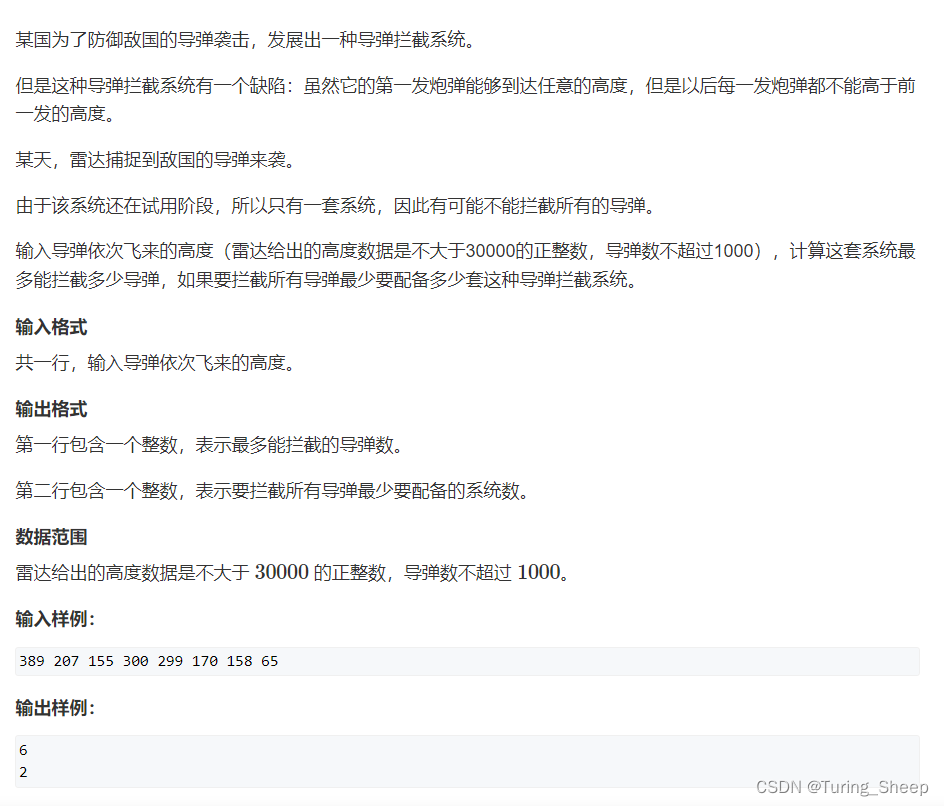
二、算法分析

这道题共分为两问，我们先看第一问。
该问的背后是一个很经典的最长单调子序列模型。
在这个模型中，我们的状态$f[i]$的定义是，以第$i$个元素为结尾的下降（上升）子序列中最长的一个子序列的长度。
状态转移方程也很简单，就是看一看以前面i个元素为结尾的最长子序列中，哪一个能够在后面接上第i个元素，然后在这些可能中取一个最大值。

$$f[i]=max(f[i],f[j]+1,f[k]+1,...)a[j]>a[i],a[k]>a[i],k<i,j<i$$

由于第一问的模型在之前的文章中有过详细地讲解，所以本篇文章重点在于讲解第二问。因此，如果大家对第一问还存在疑惑的话，建议大家去看一看作者之前写的文章：最长上升子序列优化（贪心+二分）（超级详细的讲解）

比较麻烦的是第二问，第二问的意思是，至少需要几个这样的子序列能够覆盖掉所有的元素。
在第二问中，我们使用的算法是贪心。

对于每个导弹而言，有两种选择，第一种选择就是接在当前以后的子序列的后面（如果单调性符合题意的话），第二种选择就是再创建一个新的序列。而再第一种情况当中，我们又可以做出很多种选择，因为符合单调性条件的序列可能有很多，但是具体选择哪一个是最优的选择，我们目前并不知道。

而对于贪心的题目而言，一般情况下，我们都需要先猜测出一个策略，然后对这个策略进行证明，从而体现出我们策略的正确性。在这道题中，我们想要子序列的数目最少，我们大概率是想把一个新的导弹高度接在一个现有的序列的后面。

对于这个猜测，我们可以做一个简单的证明：
假设我们的蓝色情况是在能够接在某个子序列的后面的情况下，依旧选择了自己创建一个新的子序列。我们接下的目的就是证明这种选择不是最优解。

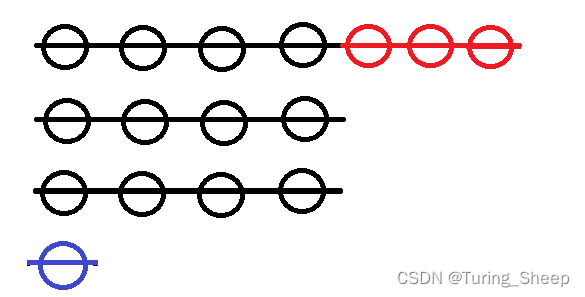
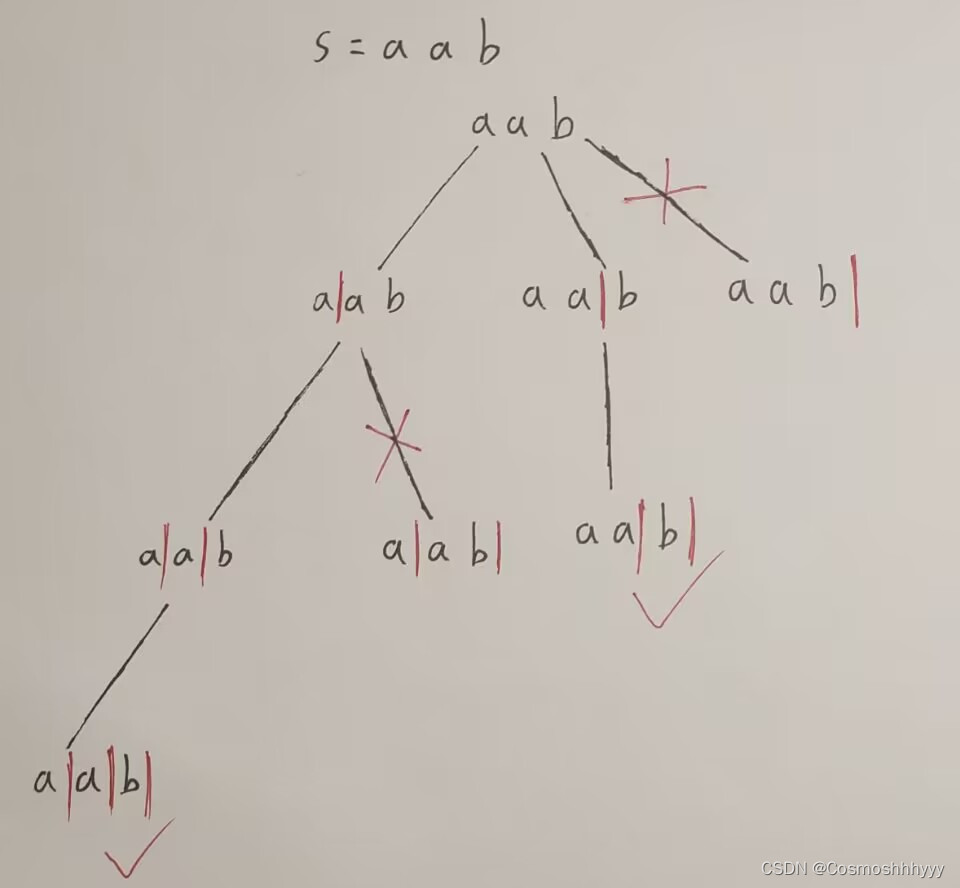
我们假设这个蓝色情况能够接在第一个子序列的红黑交界处，此时就会有两种可能，第一种就是红色无法接在蓝色的后面，第二种就是红色能够链接在二者之间。如下图所示：

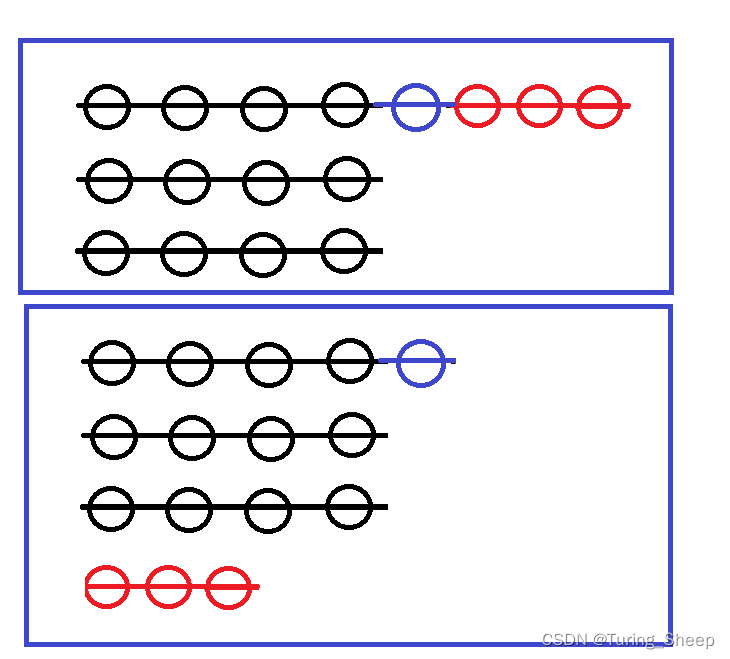
很明显，无论上述哪种可能，最后的结果都是小于等于我们假设的那种情况。也就是说存在一些情况，导致假设的最优选择不是最优的，反而我们的猜测是最优的。因此，我们的猜测是成立的。

根据上面的推到，我们已经知道，对于一个导弹而言，在满足单调性的条件下，接在已经存在的子序列的后面是最优的选择。但是我们还需要考虑一个问题，当有多个子序列符合条件时，我们接在哪一个的后面呢？

根据我们之前的经验，我们的子序列都是单调递减的，因此，将当前的导弹接在符合条件的子序列中，末尾元素最小的那一个的子序列的后面。

接着，我们尝试证明这个观点：

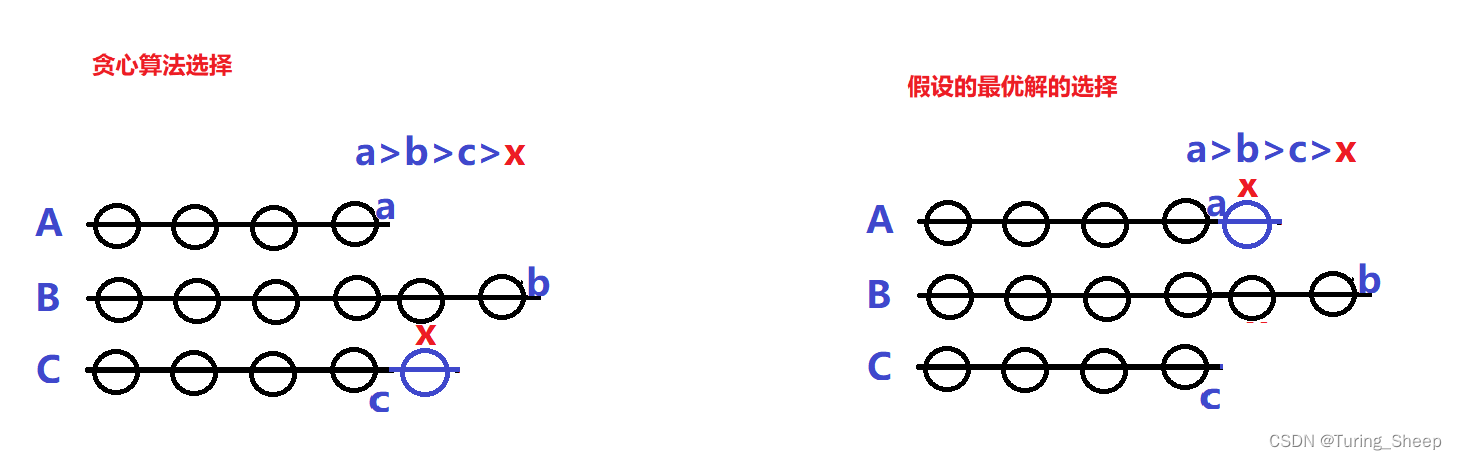
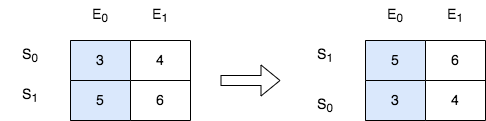
如果此时我们存在一个：y，满足y大于b，但是y小于a。此时我们就会发现，在左侧的方案中，我们可以将y接在A的子序列中，但是在假设的情况里，我们只能重新创建一个新的序列。此时我们贪心算法得到的解就小于了我们假设的情况下所得到的解，而我们想要求的是最小数量，因此，假设的情况不是最优解。

那么假设的情况里，还可以接在b的后面，这种情况下，我们再来比较一下两种选择。如果接在b的后面的话，我们的y在假设的情况中也可以接在A序列的后面，此时两种方案的结果是一样的。也就是说，我们的最优解的答案小于等于假设情况下的答案。

因此，我们的贪心策略是最优解。

那么经过一系列的分析，得出最终的做法：对于任一导弹高度，如果能够接在当前存在的子序列的后面，则接在符合条件的子序列中，末尾元素最小的那个子序列的后面。如果不能接在当前存在的序列的后面，即当前高度高于所有子序列的末尾元素，那么此时我们就再创建一个新的序列。

而这个做法恰好是最长上升子序列的贪心做法。也就是说，当我们想用尽可能少的下降子序列去覆盖整个序列的时候，这个最小值恰好等于最长上升子序列的长度。

三、代码实现

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e6+10;
int a[N],f[N],g[N];
int n;
int main()
{
    while(cin>>a[n])n++;
    int len1=0;
    for(int i=0;i<n;i++)
    {
        int l=0,r=len1;
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(f[mid]>=a[i])l=mid;
            else r=mid-1;
        }
        len1=max(len1,r+1);
        f[r+1]=a[i];
    }
    cout<<len1<<endl;
    int len2=0;
    for(int i=0;i<n;i++)
    {
        int l=0,r=len2;
        while(l<r)
        {
            int mid=l+r+1>>1;
            if(g[mid]<a[i])l=mid;
            else r=mid-1;
        }
        len2=max(len2,r+1);
        g[r+1]=a[i];
    }
    cout<<len2<<endl;
    return 0;
}