Python量化交易07——散户反买策略

news2024/9/28 1:17:48

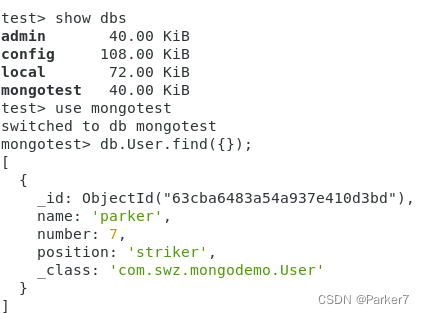
参考来源：b站up 邢不行

我们都知道在A股，散户一直是最大的韭菜贡献组群。散户买入多的个股，大概率可能跌的很惨，散户卖出多的股票，大概率会涨。

跟着北向资金买能赚钱，那么跟着散户反买，是不是也有很好的盈利效果呢？

下面用A股所有的历史数据进行测试。

数据展示

所有A股历史数据，放在一个stock文件夹里面

其中一个文件长这个样子，基本都包括正常的股票交易数据等。

代码过程

导入包，定义读取函数：

import os
import numpy as np
import pandas as pd
def load_file(path, file):
    path += file
    df = pd.read_csv(path, encoding='gbk',usecols=['股票代码','交易日期','收盘价',
                                                   '前收盘价','成交额','散户资金卖出额'],
                     parse_dates=['交易日期'], skiprows=1)
    return df

获取stock文件夹下面所有的股票代码文件名称：

file_path = r'./stock/'
file_list = os.listdir(file_path)
file_list = [f for f in file_list if '.csv' in f]
file_list[:3]

显示前三个

定义测试的时间段：

# 测试时间段
start_time = '20070101'
end_time = '20220331'

计算所有股票日交易数据的后一天，三天，五天的收益率：

dfs = []
for f in file_list:
    print(f)
    df = load_file(file_path, f)
    df['散户资金占比'] = df['散户资金卖出额'] * 10000/ df['成交额']
    for i in [1, 3, 5]:
        df['未来%d日涨跌幅' % i] = df['收盘价'].shift(-i) / df['前收盘价'].shift(-1) - 1
    df.dropna(subset=['散户资金卖出额', '成交额'], how='any',inplace=True, axis=0)
    dfs.append(df)
all_df = pd.concat(dfs, ignore_index=True)
all_df.head()

过滤一下时间：

all_df = all_df[all_df['交易日期'] >= pd.to_datetime(start_time)]
all_df = all_df[all_df['交易日期'] <= pd.to_datetime(end_time)]
all_df.shape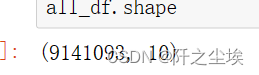

总共900w多条数据。

计算最终结果表格数据：

# ===计算最终表格
result = pd.DataFrame()  # 创建一个空的表格
for flow in np.arange(0,1,0.1):
    # 筛选出净买入大于flow的情况
    t_df = all_df[all_df['散户资金占比'] > flow]
    # 计算出现次数
    result.loc[flow, '出现次数'] = t_df.shape[0]
    # 计算未来N天数据
    for i in [1, 3, 5]:
        result.loc[flow, '未来%d日上涨次数' % i] = t_df[t_df['未来%d日涨跌幅' % i] > 0].shape[0]
        result['未来%d日上涨概率' % i] = result['未来%d日上涨次数' % i] / result['出现次数']
        result.loc[flow, '未来%d日上涨平均涨幅' % i] = t_df['未来%d日涨跌幅' % i].mean()

结果展示

由于对颜色有选择困难症，，，就用代码随机生成颜色：

import random   #定义随机生成颜色函数
def randomcolor():
    colorArr = ['1','2','3','4','5','6','7','8','9','A','B','C','D','E','F']
    color ="#"+''.join([random.choice(colorArr) for i in range(6)])
    return color

结果进行样式展示：

result.rename_axis("散户资金卖出占比") # 索引重命名
.reset_index()
.style.bar(color=randomcolor(), subset=['未来1日上涨概率','未来3日上涨概率','未来5日上涨概率'],vmin=0.3, vmax=0.9)
.bar(color=randomcolor(), subset=['未来1日上涨平均涨幅','未来3日上涨平均涨幅','未来5日上涨平均涨幅'],vmin=0.000, vmax=0.014)
.format({'出现次数':"{:.0f}",'未来1日上涨次数': "{:.0f}",'未来3日上涨次数': "{:.0f}",'未来5日上涨次数': "{:.0f}"})
.format({'未来1日上涨概率': "{:.2%}",'未来3日上涨概率': "{:.2%}",'未来5日上涨概率': "{:.2%}"})
.format({'未来1日上涨平均涨幅': "{:.3%}",'未来3日上涨平均涨幅': "{:.3%}",'未来5日上涨平均涨幅': "{:.3%}"})
.format({'散户资金卖出占比':'>{:.1f}'})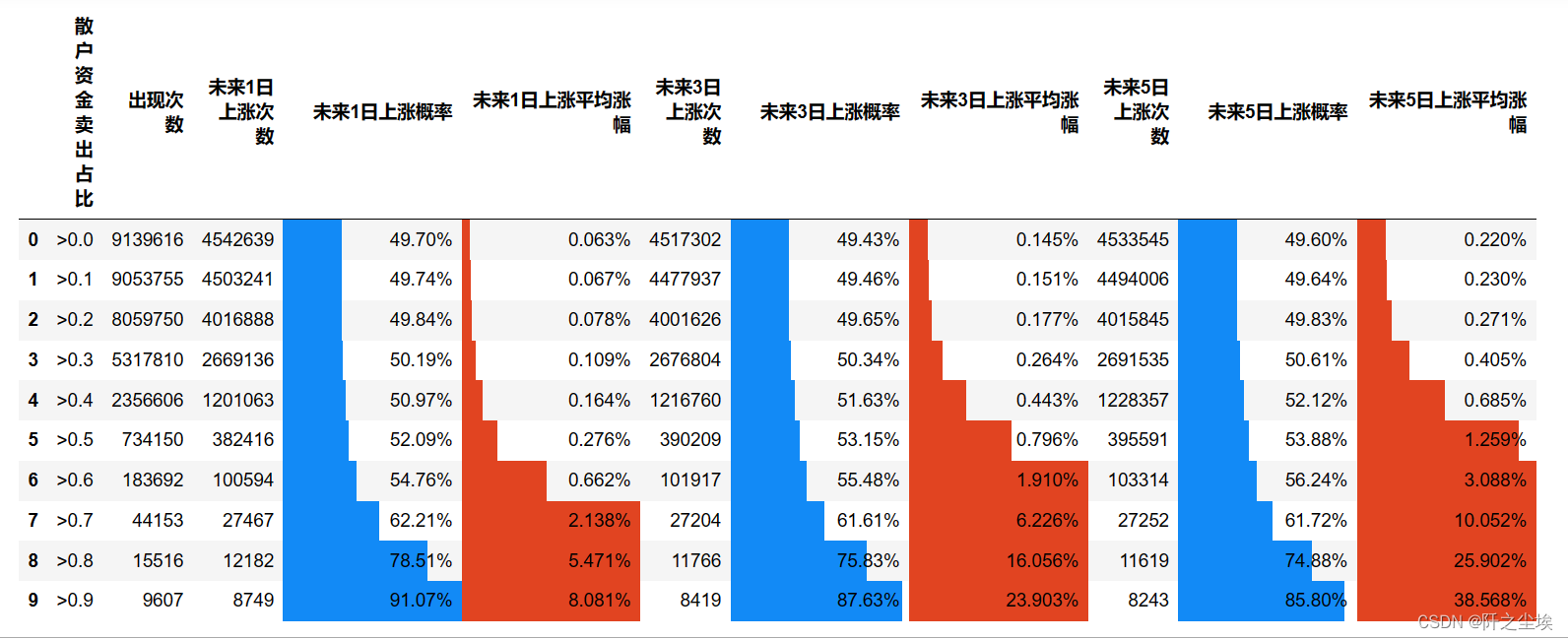

可以把计算结果进行存储：

#result.to_csv('result.csv', encoding='gbk')

我们可以看到上述结果，随着散户资金卖出的占比越来越高，在A股上所有的历史数据中出现的次数也越来越少，而且未来几日上涨的次数也越来越少。
，并且很明显，当散户资金卖出战成交额占比大于60%以上时，未来一日，三日，五日上涨的概率都明显大于50%，而且获得的平均涨幅的收益也是较高的。并且随着这个散户卖出占比比例越高，这个胜率和涨幅也越来越高。
很明显，跟着散户反卖这个策略是能够获得盈利的。

回测结果

利用这个策略，我们实施了一个这样的交易逻辑，即每日选择所有股票中，散户卖出占比最高的三只股票进行买入，仓位分散为1/3，每三天重新计算卖出占比，轮流换一次仓。
这个策略的代码会很复杂，需要借助专门的量化框架来进行回测。
这里就给出最终的回撤结果的一个画图展示：

import pandas as pd
import matplotlib.pyplot as plt
equity = pd.read_csv(r'回测结果_event_资金流_1_3_3_3.csv', encoding='gbk', parse_dates=['交易日期'])
equity.set_index(['交易日期'], inplace=True)
equity.head()

画图：

equity[['净值', '基准净值']].plot(figsize=(9, 5), grid=False, fontsize=20)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.savefig(r'散户反买策略.png')
plt.show()