回溯——排列组合

news2024/11/16 6:56:03

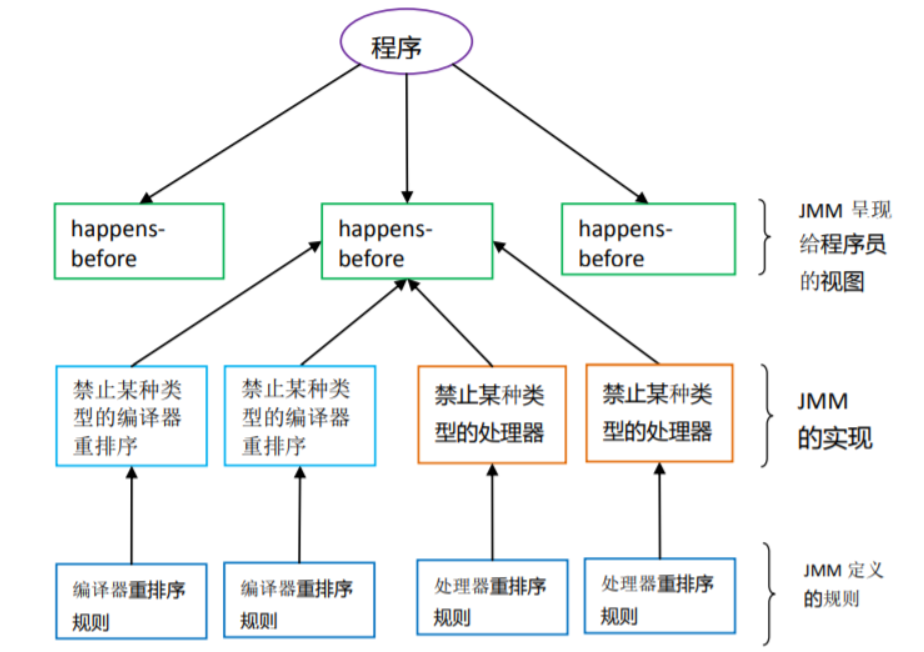
1.组合(结果不区分顺序)

1.同一个集合求组合需要startindex

需要startindex

1.元素可以重复使用

startindex为i

例：

lc39[组合总和] 给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

  • 所有数字（包括 target）都是正整数。
  • 解集不能包含重复的组合。

示例 1： 输入：candidates = [2,3,6,7], target = 7, 所求解集为： [ [7], [2,2,3]

示例 2： 输入：candidates = [2,3,5], target = 8, 所求解集为： [2,2,2,2],2,3,3],3,5]

class Solution {

    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> temp = new LinkedList<>();
    int[] candidates;

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        this.candidates = candidates;
        helper(0,target);
        return res;
    }

    void helper(int index,int target){
        if (target == 0){
            res.add(new LinkedList<>(temp));
            return;
        }

        for (int i = index; i < candidates.length; i++) {
            temp.add(candidates[i]);
            if (target - candidates[i] >= 0){
                helper(i,target - candidates[i]);
            }
            temp.removeLast();
        }
    }
   
}

关于自己的错误解答：index从0开始。

例如candidates = [1,2]，

第一层为1，第二层可以为1，2。

第一层为2，第二层还是可以为1，2。

可以看到其中的[1,2] [2,1]是重复了的。

2.元素不能重复使用

startindex为i+1

lc77[组合] 给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],]

public class Solution {
    List<List<Integer>> res;
    LinkedList<Integer> path;
    int n;
    int k;

    public List<List<Integer>> combine(int n, int k) {
        res = new ArrayList<>();
        if (k <= 0 || n < k) {
            return res;
        }
        this.k = k;
        this.n = n;
        path = new LinkedList<>();
        dfs(1);
        return res;
    }

    private void dfs(int index) {
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }
        //不是i <= n的原因:输入6,4，如果目前结果集中已有1个元素，则只需要遍历到4（上限）即可，因为从5/6开始无法凑够4个数
        //也就是最小可选范围需要小于k - size
        //最小可选范围 = n - 上限 + 1
        //n - 上限 + 1 = k - size
        //上限 = n + 1 - (k - size)
        for (int i = index; i <= n + 1 - (k - path.size()); i++) {
            path.addLast(i);
            dfs(i + 1);
            path.removeLast();
        }
    }
}

lc40[组合总和II] 给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates中的每个数字在每个组合中只能使用一次。

说明：

  • 所有数字都是正整数。
  • 解集不能包含重复的组合。

示例 1: 输入: candidates = [10,1,2,7,6,1,5], target = 8, 所求解集为: [[1, 7],[1, 2, 5],[2, 6],[1, 1, 6]]

示例 2: 输入: candidates = [2,5,2,1,2], target = 5, 所求解集为: [[1,2,2],[5]]

需要注意数组元素重复，但结果不允许重复。所以需要对于树层去重，树枝不需去重。

class Solution {

    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> temp = new LinkedList<>();
    int[] candidates;
    boolean[] used;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        this.candidates = candidates;
        Arrays.sort(candidates);
        helper(0,target);
        return res;
    }

    void helper(int index,int target){
        if (target == 0){
            res.add(new ArrayList<>(temp));
            return;
        }


        for (int i = index; i < candidates.length && target - candidates[i] >= 0; i++) {
            //当i=index时，说明遇到的是同一层的第一个，i>index时，遇到的是同一层的非第一个，需要跳过。
            if (i > index && candidates[i - 1] == candidates[i]){
                continue;
            }
            temp.add(candidates[i]);
            helper(i + 1,target - candidates[i]);
            temp.removeLast();
        }
    }
}

//使用标记数组，认真看，还是很好理解的
class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> ans = new ArrayList<>();
//    标志数组，用来辅助判断同层节点是否已经遍历
    boolean[] used;
    int sum = 0;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        used = new boolean[candidates.length];
        // 为了将重复的数字都放到一起，所以先进行排序
        Arrays.sort(candidates);
        backTracking(candidates, target, 0);
        return ans;
    }

    private void backTracking(int[] candidates, int target, int startIndex) {
        if (sum == target) {
            ans.add(new ArrayList(path));
        }
        for (int i = startIndex; i < candidates.length; i++) {
            if (sum + candidates[i] > target) {
                break;
            }
            //如果是同一层，used在上一步的回溯中设为false，相同的数跳过
            //同一枝，used是true，相同的数不需要跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
                continue;
            }
            used[i] = true;
            sum += candidates[i];
            path.add(candidates[i]);
            // 每个节点仅能选择一次，所以从下一位开始
            backTracking(candidates, target, i + 1);
            used[i] = false;
            sum -= candidates[i];
            path.removeLast();
        }
    }
}

lc216[组合总和III] 找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

  • 所有数字都是正整数。
  • 解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

class Solution {

    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> temp = new LinkedList<>();
    int n;
    int k;

    public List<List<Integer>> combinationSum3(int k, int n) {
        this.n = n;
        this.k = k;
        dfs(1,0);
        return res;
    }

    void dfs(int index,int count){

        if (count == n && temp.size() == k){
            res.add(new LinkedList<>(temp));
            return;
        }
        for (int i = index; i <= 9; i++) {
            temp.add(i);
            dfs(i + 1,count+i);
            temp.removeLast();
        }
    }
}

2.不同集合求组合不需要startindex

lc17[电话号码的数字组合] 给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

示例:

  • 输入：“23”
  • 输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
class Solution {
    //设置全局列表存储最后的结果
    List<String> list = new ArrayList<>();
    //每次迭代获取一个字符串，所以会设计大量的字符串拼接，所以这里选择更为高效的 StringBuild
    StringBuilder temp = new StringBuilder();
    //初始对应所有的数字，为了直接对应2-9，新增了两个无效的字符串""
    String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    String digits;
    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) {
            return list;
        }
        this.digits = digits;
        //迭代处理
        backTracking(0);
        return list;
    }

    void backTracking(int index){
        if (index == digits.length()){
            list.add(new String(temp));
            return;
        }
        
        String curString = numString[digits.charAt(index) - '0'];
        for (int i = 0; i < curString.length(); i++) {
            temp.append(curString.charAt(i));
            backTracking(index + 1);
            temp.deleteCharAt(temp.length() - 1);
        }
    }
}

3.子集(特殊的组合)

如果把子集问题、组合问题、排列问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点

lc78[子集] 给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例: 输入: nums = [1,2,3] 输出: [[3],[1],[2],1,2,3],1,3],2,3],1,2]]

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    Deque<Integer> queue = new ArrayDeque<>();
    int[] nums;

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        if (nums.length == 0){
            return res;
        }
        this.nums = nums;
        dfs(0);
        return res;
    }

    void dfs(int index){
        if (index <= nums.length){
            res.add(new ArrayList<>(queue));
        }
        for (int i = index; i < nums.length; i++) {
            queue.add(nums[i]);
            dfs(i + 1);
            queue.removeLast();
        }
    }
}

lc90[子集II] 给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

  • 输入: [1,2,2]
  • 输出: [2], [1], [1,2,2], [2,2], [1,2], []
class Solution {

    List<List<Integer>> res = new LinkedList<>();
    Deque<Integer> queue = new ArrayDeque<>();
    int[] nums;

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        if (nums.length == 0){
            return res;
        }
        this.nums = nums;
        Arrays.sort(nums);
        dfs(0);
        return res;
    }


    void dfs(int index){
        if (index <= nums.length){
            res.add(new ArrayList<>(queue));
        }

        for (int i = index; i < nums.length; i++) {
            //只留取同一层的第一个相同的数。
            //当i大于index，且与i-1相等说明同一层中当前数与前一个数相等。
            if (index < i && nums[i] == nums[i - 1]){
                continue;
            }
            queue.add(nums[i]);
            dfs(i + 1);
            queue.removeLast();
        }
    }
}

lc491[递增子序列] 给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例:

  • 输入: [4, 6, 7, 7]
  • 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:

  • 给定数组的长度不会超过15。
  • 数组中的整数范围是 [-100,100]。
  • 给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

可以使用used数组，上述情况中属于纵向递归可以重复，横向遍历不能重复，所以used写在函数里，每次递归会创建新的used数组。

如果将used写在外边(全局变量)，则在整棵树中都不能重复

//要求递增所以不能给原数组排序
class Solution {
    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtracking(nums,0);
        return res;
    }

    private void backtracking (int[] nums, int start) {
        if (path.size() > 1) {
            res.add(new ArrayList<>(path));
        }

        //题目中-100 <= nums[i] <= 100
        int[] used = new int[201];
        for (int i = start; i < nums.length; i++) {
            if (!path.isEmpty() && nums[i] < path.get(path.size() - 1) ||
                    (used[nums[i] + 100] == 1)) {
            	continue;   
            }
            used[nums[i] + 100] = 1;
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

并且，原数组中有重复数的时候不能直接用数组下标来标记数字是否使用。例如原数组nums[] = {1,1}，used[] = {1,0}只能说明第一个1被使用，第二个1还是可以使用，失去了去重的意义。以496题为例可以用：used[nums[i] + 100] == 1来标记。

此题也可以使用set集合来去重，但set涉及到hash计算，效率远低于数组，在数组范围允许的情况下最好还是使用数组较好。

4.切割问题(特殊的组合)

lc131[分割回文串] 给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: “aab” 输出: [ [“aa”,“b”], [“a”,“a”,“b”]

切割问题，也可以抽象为一棵树形结构，如图：

[(img-YO8t7Jj8-1674273086023)(D:\MK图片\131.分割回文串.jpg)]

递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

此时可以发现，切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。

class Solution {
    List<List<String>> lists = new ArrayList<>();
    Deque<String> deque = new LinkedList<>();

    public List<List<String>> partition(String s) {
        backTracking(s, 0);
        return lists;
    }

    private void backTracking(String s, int startIndex) {
        //如果起始位置大于s的大小，说明找到了一组分割方案
        if (startIndex >= s.length()) {
            lists.add(new ArrayList(deque));
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            //如果是回文子串，则记录
            if (isPalindrome(s, startIndex, i)) {
                String str = s.substring(startIndex, i + 1);
                deque.addLast(str);
            } else {
                continue;
            }
            //起始位置后移，保证不重复
            backTracking(s, i + 1);
            deque.removeLast();
        }
    }
    //判断是否是回文串
    private boolean isPalindrome(String s, int startIndex, int end) {
        for (int i = startIndex, j = end; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}

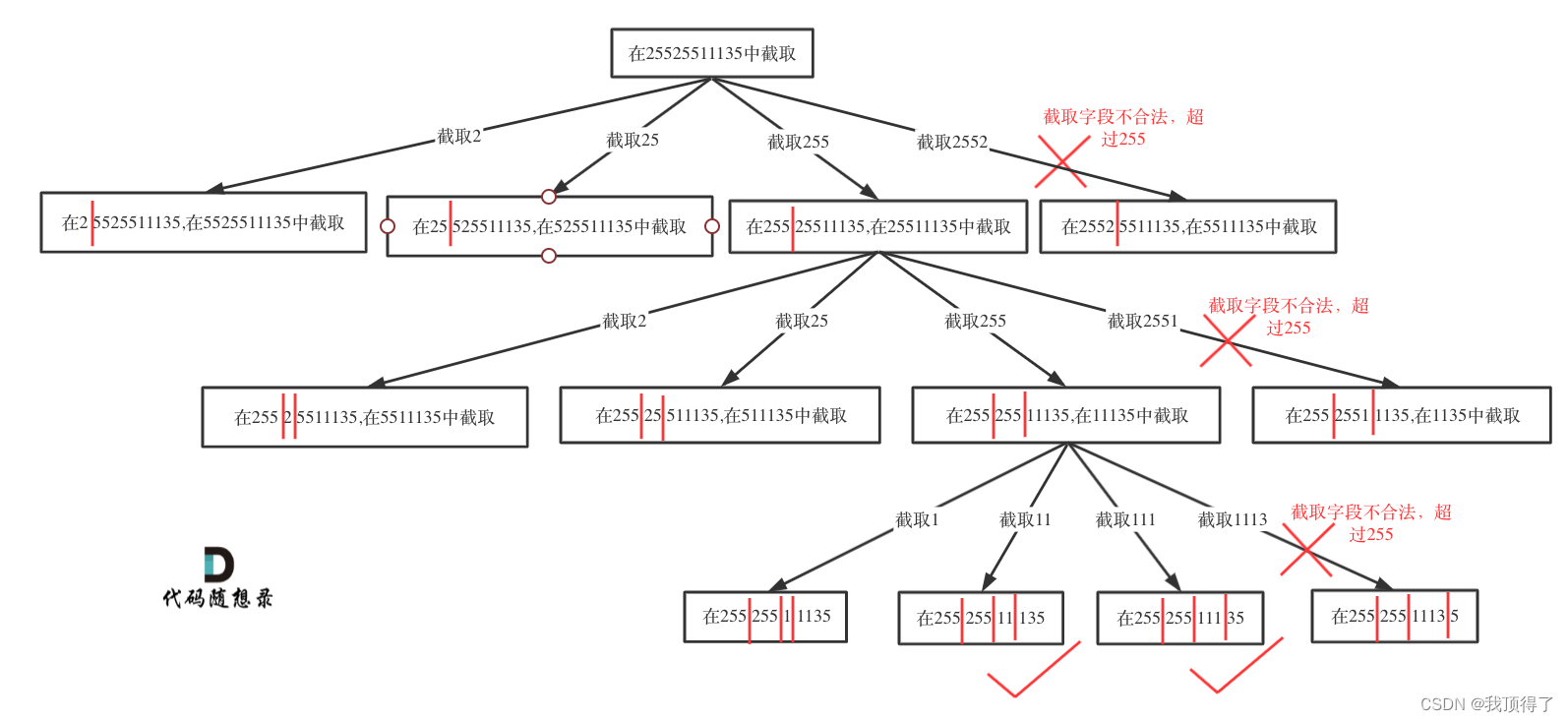
lc93[分割回文串] 给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

有效的 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

例如：“0.1.2.201” 和 “192.168.1.1” 是 有效的 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是 无效的 IP 地址。

示例 1：

  • 输入：s = “25525511135”
  • 输出：[“255.255.11.135”,“255.255.111.35”]
class Solution {

    List<String> res = new ArrayList<>();
    Deque<String> path = new ArrayDeque<>(4);
    String s;
    public List<String> restoreIpAddresses(String s) {
        this.s = s;
        dfs(0, 4);
        return res;
    }

    void dfs(int index, int sum){
        //当前有4段且长度刚好为s长度
        if (sum == 0 && index == s.length()){
            res.add(String.join(".", path));
        }

        for (int i = index; i < s.length(); i++) {
            //长度小于三且是回文串
            if (i - index < 3 && judgeNumber(s,index,i)){
                path.add(s.substring(index,i+1));
                dfs(i+1,sum-1);
                path.removeLast();
            }
        }

    }

    public boolean judgeNumber(String s, int left, int right){
        int len = right - left + 1;
        //当前为0开头的且长度大于1的数字需要剪枝
        if(len>1 && s.charAt(left)=='0'){
            return false;
        }
        //将当前截取的字符串转化成数字
        int res = len<=0 ? 0 : Integer.parseInt(s.substring(left, right+1));
        //判断截取到的数字是否符合
        return res>=0 && res<=255;
    }
}

在这里插入图片描述

2.排列(结果区分顺序)

首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

但排列问题需要一个used数组，标记已经选择的元素。

lc46[全排列] 给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

  • 输入: [1,2,3]
  • 输出: [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]
class Solution {

    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
    boolean[] used;
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0){
            return result;
        }
        used = new boolean[nums.length];
        permuteHelper(nums);
        return result;
    }

    private void permuteHelper(int[] nums){
        if (path.size() == nums.length){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++){
            if (used[i]){
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteHelper(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

// 解法2：通过判断path中是否存在数字，排除已经选择的数字
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0) return result;
        backtrack(nums, path);
        return result;
    }
    
    public void backtrack(int[] nums, LinkedList<Integer> path) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
        }
        for (int i =0; i < nums.length; i++) {
            // 如果path中已有，则跳过
            if (path.contains(nums[i])) {
                continue;
            } 
            path.add(nums[i]);
            backtrack(nums, path);
            path.removeLast();
        }
    }
}

lc47[全排列II] 给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

  • 输入：nums = [1,1,2]
  • 输出： [[1,1,2], [1,2,1], [2,1,1]]

示例 2：

  • 输入：nums = [1,2,3]
  • 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10
//第一种相对较好理解
class Solution {
    private List<List<Integer>> res = new ArrayList<>();
    private List<Integer> path = new ArrayList<>();
    private boolean[] used = null;

    public List<List<Integer>> permuteUnique(int[] nums) {
        used = new boolean[nums.length];
        Arrays.sort(nums);
        backtracking(nums);
        return res;
    }

    public void backtracking(int[] nums) {
        if (path.size() == nums.length) {
            res.add(new ArrayList<>(path));
            return;
        }
        
        HashSet<Integer> hashSet = new HashSet<>();//层去重，相比普通的多了个层去重
        //除了使用set去重也可以使用used[nums[i] + 100] == true来去重。
        for (int i = 0; i < nums.length; i++) {
            if (hashSet.contains(nums[i]))
                continue;
            if (used[i])//枝去重，起startindex的作用
                continue;
            hashSet.add(nums[i]);//记录元素
            used[i] = true;
            path.add(nums[i]);
            backtracking(nums);
            path.remove(path.size() - 1);
            used[i] = false;
        }
    }
}


//第二种
class Solution {
    //存放结果
    List<List<Integer>> result = new ArrayList<>();
    //暂存结果
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used = new boolean[nums.length];
        Arrays.fill(used, false);
        Arrays.sort(nums);
        backTrack(nums, used);
        return result;
    }

    private void backTrack(int[] nums, boolean[] used) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
/*
for循环保证了从数组中从前往后一个一个取值，再用if判断条件。所以nums[i - 1]一定比nums[i]先被取值和判断。如果nums[i - 1]被取值了，used[i - 1]会被置true，只有当递归再回退到这一层时再将它置false。所以当used[i - 1] == true时，说明nums[i - 1]和nums[i]分别属于两层递归中（在同一树枝中），也就是我们要用这两个数分别放在数组的两个位置，这时不需要去重。但是当used[i - 1] == false时，说明nums[i - 1]和nums[i]属于同一层递归中，此时需要去重。
*/
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            //如果同⼀树枝nums[i]没使⽤过，开始处理
            if (used[i] == false) {
                used[i] = true;
                path.add(nums[i]);
                backTrack(nums, used);
                path.remove(path.size() - 1);//回溯
                used[i] = false;//回溯
            }
        }
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/175209.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C进阶_内存库函数_和这群虫豸在一起，怎能搞好政治呢？

C进阶_内存库函数_和这群虫豸在一起，怎能搞好政治呢？

其实之前我写过这篇……但是不够详细&#xff01;今天重新写一下。 目录 memcpy 模拟实现memcpy memmove 模拟实现memmove memcpy 它的函数原型是&#xff1a; void * memcpy ( void * destination, const void * source, size_t num ); 查阅文档它的文档&#xff1a; C…
阅读更多...
帮助有一定计算机基础的人 快速复习并重新拾起C语言基础（数据类型篇）

帮助有一定计算机基础的人 快速复习并重新拾起C语言基础（数据类型篇）

数据类型 帮助有一定计算机基础的人 快速复习并重新拾起C语言基础C语言数据类型分类基本数据类型整型类型的分类整型类型的基本用法有符号与无符号的区别字符型数据转义字符char 类型的范围浮点数类型数据字符串常量字符串输入之scanf函数字符输入输出函数算术运算符比较运算符…
阅读更多...
SPI-读写串行FLASH

SPI-读写串行FLASH

简介 是由摩托罗拉公司提出的通讯协议&#xff0c;即串行外围设备接口&#xff0c;是一种高速全双工的通信总线。它被广 泛地使用在ADC、LCD等设备与MCU间&#xff0c;要求通讯速率较高的场合。特性 1、全双工&#xff08;即可以同时收发&#xff09;2、最少需要占用4条线&…
阅读更多...
图解统计学 10 | 贝叶斯公式与全概率公式

图解统计学 10 | 贝叶斯公式与全概率公式

文章目录概率联合概率条件概率全概率公式贝叶斯公式过年了&#xff0c;作为水果店老板的我们&#xff0c;一共进了三种水果&#xff0c;其中&#xff1a;西瓜&#xff1a;50个 香蕉&#xff1a;30个 橙子&#xff1a;20个 为了方便顾客挑选&#xff0c;放在如下的格子里&…
阅读更多...
[Android]Shape Drawable

[Android]Shape Drawable

ShapeDrawable可以理解为通过颜色来构造的图形 <android.widget.Buttonandroid:id"id/button1"android:layout_width"wrap_content"android:layout_height"wrap_content"android:text"Button"android:background"drawable/sha…
阅读更多...
MongoDB学习笔记【part4】SpringBoot集成MongoDB、MongoTemplate开发CURD

MongoDB学习笔记【part4】SpringBoot集成MongoDB、MongoTemplate开发CURD

一、Spring Boot 集成 Mongodb spring-data-mongodb 提供了 MongoTemplate 与 MongoRepository 两种方式访问mongodb&#xff0c;MongoRepository 操作简单&#xff0c;但 MongoTemplate 更加灵活&#xff0c;我们在项目中可以灵活使用这两种方式操作mongodb。 第一步&#x…
阅读更多...
铸造性能监控平台【grafana+influxdb/prometheus+Linux/Windows】

铸造性能监控平台【grafana+influxdb/prometheus+Linux/Windows】

目录一、grafanainfluxdbjmeter1、前言2、安装grafana和influxdb3、启动grafana4、访问grafana5、启动influxdb6、配置influxdb和jmeter7、在grafana中显示数据8、其他模板二、grafanaprometheusexporter1、前言2、grafana启动3、exporter安装与运行4、prometheus安装与运行5、…
阅读更多...
代码随想录算法训练营第23天 二叉树 java : 669. 修剪二叉搜索树108.将有序数组转换为二叉搜索树538.把二叉搜索树转换为累加树

代码随想录算法训练营第23天 二叉树 java : 669. 修剪二叉搜索树108.将有序数组转换为二叉搜索树538.把二叉搜索树转换为累加树

文章目录LeetCode 669. 修剪二叉搜索树题目讲解思路LeetCode 108.将有序数组转换为二叉搜索树题目讲解思路LeetCode 538.把二叉搜索树转换为累加树题解思路总结LeetCode 669. 修剪二叉搜索树 题目讲解 思路 在1到3的区间选择 元素 如何超过3 或者 小于1 如果小于1 叫要考虑 …
阅读更多...
NeRF: Representing Scenesas Neural Radiance Fieldsfor View Synthesis论文阅读

NeRF: Representing Scenesas Neural Radiance Fieldsfor View Synthesis论文阅读

注意&#xff1a;和很多文章一样&#xff0c;在Google搜索到最终版本时&#xff0c;有链接指出其有7个历史版本&#xff0c;但内容较详细的却不是最终版本&#xff0c;而是ECCV (2020)版&#xff0c;阅读时可以两个版本配合着阅读。 1. 摘要 我们提出了一种方法&#xff0c;通…
阅读更多...
202301读书笔记|《命运》蔡崇达

202301读书笔记|《命运》蔡崇达

202301读书笔记|《命运》蔡崇达 《命运》是我读的蔡崇达的第二本书&#xff0c;第一本是《皮囊》印象最深的一句就是“肉体是拿来用来的&#xff0c;不是拿来伺候的。” 当时读完第一本就很受触动&#xff0c;这一次读完《命运》依然很触动我。作者真的很厉害&#xff0c;这个故…
阅读更多...
SpringBoot看这一篇文章就够了

SpringBoot看这一篇文章就够了

第一章 SpringBoot简介 第1节 SpringBoot是什么 1 21.SpringBoot是一个可以快速创建可运行的、独立的、生产级的基于Spring的应用程序 2.SpringBoot采用一种约定优于配置的设计理念,可以快速让用户创建出一个可运行的基于Spring的应用第2节 SpringBoot的优势 1 2 3 4 51.快速构…
阅读更多...
nacos源码解析==SPI和spring.factories机制-服务注册-心跳发送-服务拉取-服务调用

nacos源码解析==SPI和spring.factories机制-服务注册-心跳发送-服务拉取-服务调用

Spring.Factories这种机制实际上是仿照java中的SPI扩展机制实现的 springboot核心基础之spring.factories机制 - 知乎 SpringBoot1IDEA编写一个自己的starter_一个java开发的博客-CSDN博客_idea创建spring starter spring-cloud-starter-alibaba-nacos-discovery 将要注册到…
阅读更多...
know sth. new 大话C#的进阶必知点解析第1章 第5节 名贵中药材程序WPF显示图片报错，找不到资源？ 什么原因

know sth. new 大话C#的进阶必知点解析第1章 第5节 名贵中药材程序WPF显示图片报错，找不到资源？ 什么原因

1 Ui布局代码&#xff1b; 布局方面&#xff0c;主要还是继承了原先的布局方式。包括图片的展示&#xff0c;也是用了最外层border边框的方式&#xff0c;边框加入背景颜色方式的图片展示&#xff1b; 去把目标图片进行显示出来&#xff0c;这个没有太多技术含量。 至于图片的…
阅读更多...
Spring Boot操作数据库学习之整合Druid

Spring Boot操作数据库学习之整合Druid

文章目录一 Druid 简介二 配置数据源创建项目步骤及数据库内容三 整合操作3.1 添加Druid数据源依赖3.2 编写配置文件3.3 测试3.4 自定义绑定数据源设置3.5 导入Log4j的依赖&配置日志输出3.6 添加DruidDataSource组件3.7 测试3.8 配置 Druid 数据源监控3.9 配置过滤器一 Dru…
阅读更多...
SAPIEN PowerShell Studio 介绍

SAPIEN PowerShell Studio 介绍

PowerShell Studio是一款优秀的基于PowerShell研发的脚本编辑器&#xff0c;它拥有全新的代码分析、智能预选、xaml支持功能&#xff0c;能够给用户提供一套完整的软件开发环境&#xff0c;让用户能够更加轻松的工作&#xff0c;这样一来大家开发项目的效率就会大大提升。创建模…
阅读更多...
Day866.binlogredoLog -MySQL实战

Day866.binlogredoLog -MySQL实战

日志系统 Hi&#xff0c;我是阿昌&#xff0c;今天学习的是关于MySql的binlog&redoLog的内容。 一条查询语句的执行过程一般是经过连接器、分析器、优化器、执行器等功能模块&#xff0c;最后到达存储引擎。 那么&#xff0c;一条更新语句的执行流程又是怎样的呢&#x…
阅读更多...
人大金仓数据库的用户与角色

人大金仓数据库的用户与角色

创建用户 create user 用户名 授予用户创建数据库权限 alter user 用户名 要给的权限 然后查看用户信息 \du 用户名 设置用户密码 没有口令不能登录 alter user 用户名 password ‘kingbase’; 修改用户的并发连接数 alter user 用户 connection limit 要设置的连接数; 修改…
阅读更多...
as-if-serialhappens-before

as-if-serialhappens-before

一、as-if-serialas-if-serial语义的意思是&#xff1a;不管怎么重排序&#xff08;编译器和处理器为了提高并行度&#xff09;&#xff0c;&#xff08;单线程&#xff09;程序的执行结果不能被改变。编译器、runtime和处理器都必须遵守as-if-serial语义。 为了遵守as-if-seri…
阅读更多...
java类成员/final/static都涉及到了2023025

java类成员/final/static都涉及到了2023025

类成员&#xff1a; 在Java类里只能包含成员变量、方法、构造器、初始化块、内部类&#xff08;包括接口、枚举&#xff09;这5种成员&#xff0c;目前已经介绍了前面4种&#xff0c;其中static可以修饰成员变量、方法、初始化块、内部类&#xff08;包括接口&#xff0c;枚举&…
阅读更多...
显示器的相关知识

显示器的相关知识

目录 显示器的作用 显示器的尺寸 人眼的可视角度 显示器的分辨率 显示器的刷新率 显示器的灰阶响应时间 显示器的色域 显示器的色深 显示器的色准 显示器的HDR参数 显示器的面板 画面撕裂 前言 导致画面撕裂的原因 防画面撕裂技术 视频的码率 显示器的作用 把…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023