过年了，作为水果店老板的我们，一共进了三种水果，其中：

西瓜：50个

香蕉：30个

橙子：20个

为了方便顾客挑选，放在如下的格子里，每个格子放一个水果，总共 100 个

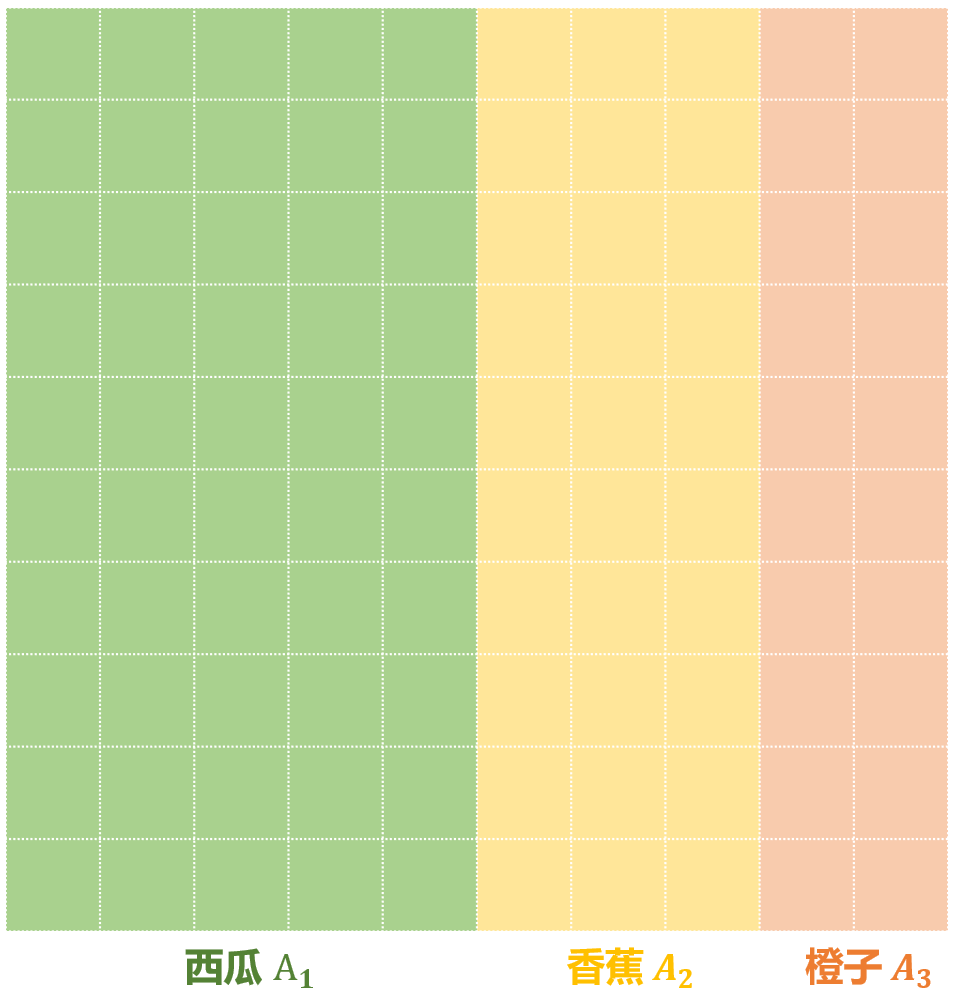
概率

现在有一人前来买水果，那么可以算出他买某种水果的概率：

西瓜：$P(A_1)=50/100=0.5$

香蕉：$P(A_2)=30/100=0.3$

橙子：$P(A_3)=20/100=0.2$

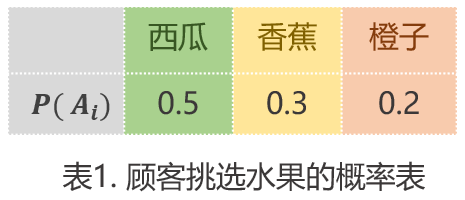
我们统计下买某种水果的概率，并记录为表1

联合概率

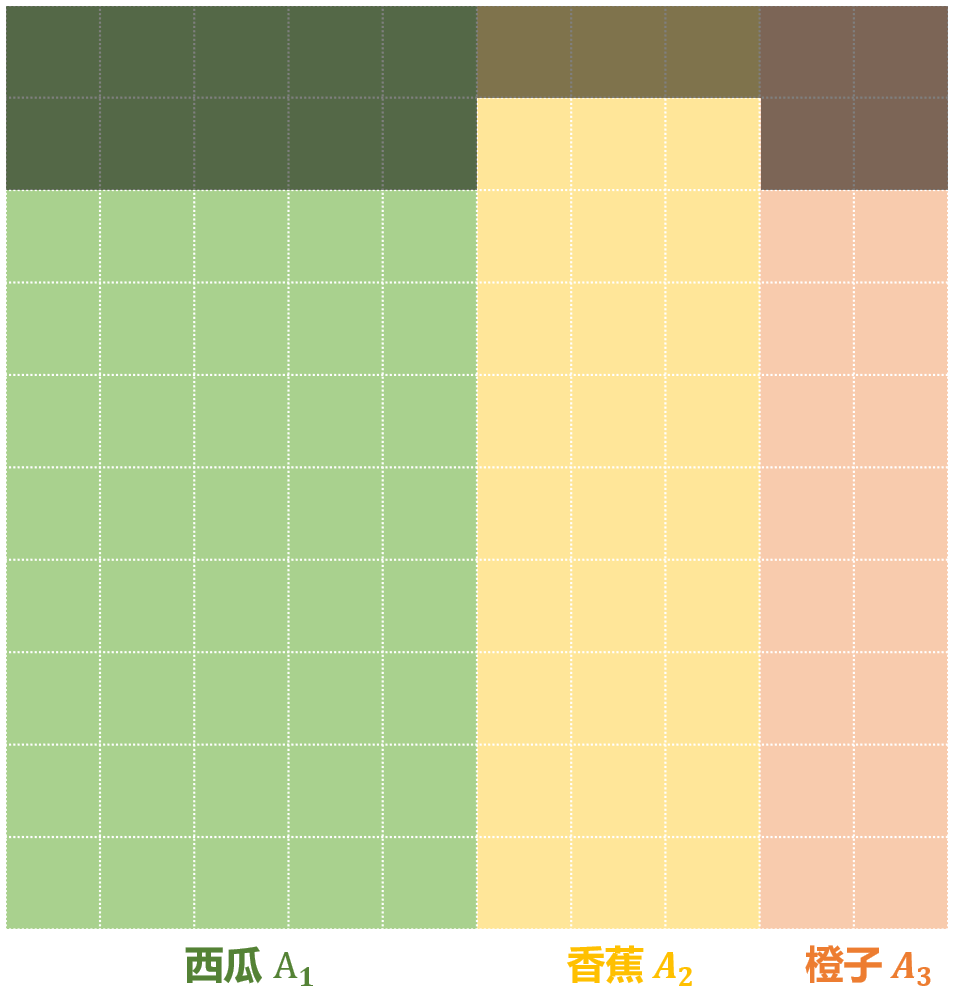
水果质量乘次不齐，会有少量的坏果，顾客一般从外观难以分辨。

但是作为经验老道的老板，大概知道有几个坏果，用较深的颜色统计每种水果中的坏果，从图中可以看到：

西瓜里有 10 个坏果

香蕉里有 3 个坏果

橙子里有 4 个坏果

那么顾客既选西瓜又选到坏果的概率是

西瓜：$P(A_1,B)=10/100=0.1$

这里，顾客既选西瓜A_1又选到坏果B的概率用P(x_1,y)表示，逗号用来表示两件事同时发生。

其他的类似：

香蕉：$P(A_2,B)=3/100=0.03$

橙子：$P(A_3,B)=4/100=0.04$

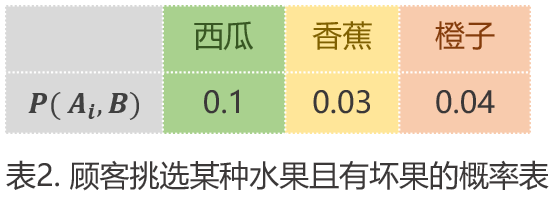
我们统计下顾客挑选某种水果且有坏果的概率表，记录为表2

条件概率

与之前不同，顾客现在就想买颗西瓜，他选到坏果的概率是多少？

西瓜：$P(B|A_1)=10/50=0.2$

这里，顾客从西瓜里选到坏果的概率用 $P(B|A_1)$ 表示，

其中 |表示在 A_1发生的前提下又发生B的概率。

其他水果：

香蕉：$P(B|A_2)=3/30=0.1$

橙子：$P(B|A_3)=4/20=0.2$

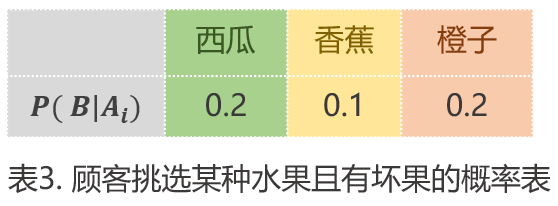
我们统计下顾客从某种水果挑选到坏果的概率表，记录为表3

现在我们把以上三张表整理成一张表

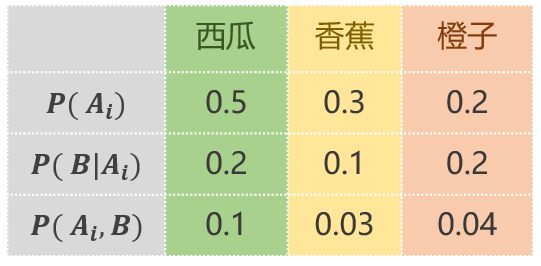
我们会惊奇的发现一个规律：

西瓜：$P(A_1,B)=P(A_1)P(B|A_1)=0.5\times 0.2=0.1$

香蕉：$P(A_2,B)=P(A_2)P(B|A_2)=0.3\times 0.1=0.03$

橙子：$P(A_3,B)=P(A_3)P(B|A_3)=0.2\times 0.5=0.04$

恭喜你，已经发现了联合概率公式：

$P(A_i,B)=P(A_i)P(B|A_i)$

利用幼儿园的乘除法，可以转化为：

$P(B|A_i)=\frac{P(A_i,B)}{P(A_i)}$

这就是所谓的条件概率公式。

条件概率也可以用集合图表示，其实就是用 $P(A_i,B)$ 联合概率(交集) 除以 $P(A_i)$

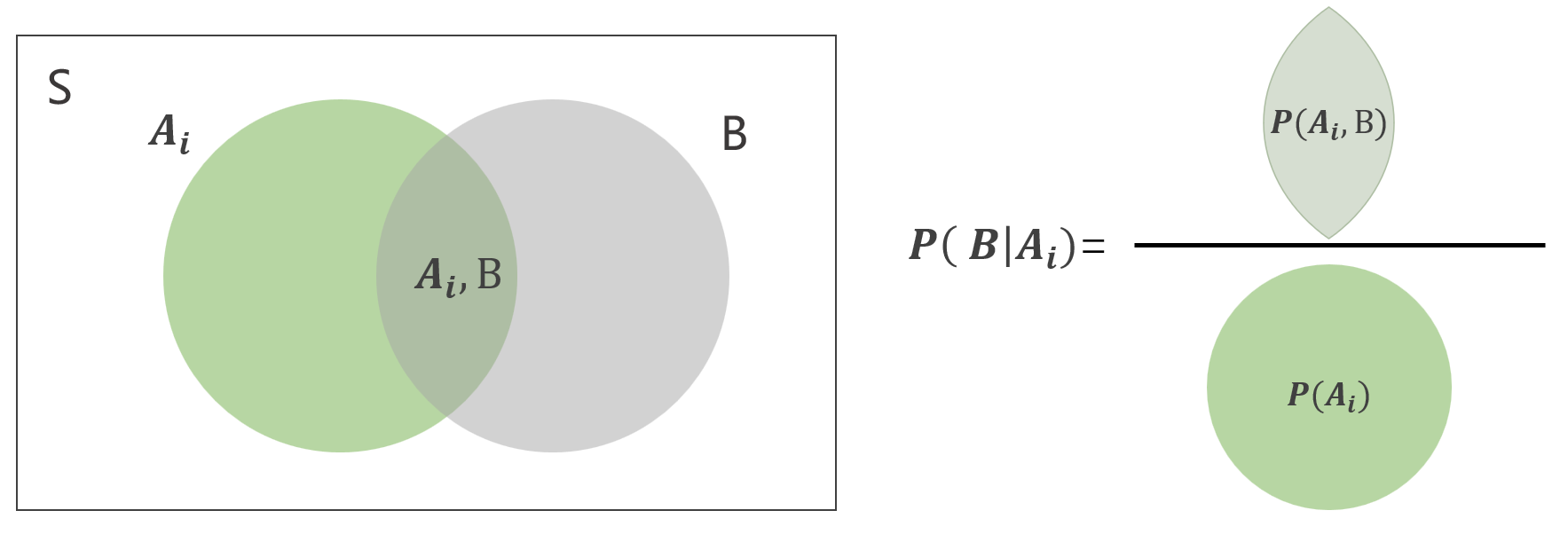
全概率公式

现在统计下顾客选到坏果的概率为：

$P(B)=(10+3+4)/100=0.17$

再拿过来刚刚的统计表

我们现在发现又一条规律：

$P(B)=P(A_1,B)+P(A_2,B)+P(A_3,B)=0.1+0.03+0.04=0.17$

在现实生活中，我们并不能直接得到 $P(A_i,B)$ 的值，或者获取难度太大。

一般只能获得某个事件发生的概率 $P(A_i)$ 或在 A 事件发生后 B 事件发生的条件概率 $P(B|A_i)$ ,

因此，代入刚刚推导出的联合概率公式，

也就是使用$P(A_i)P(B|A_i)$ 来指代$P(A_i,B)$ ，得到：

$$\begin{gathered} P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)P(B|A_3) \\ =0.5\times 0.2+0.3\times 0.1+0.2\times 0.2=0.17 \end{gathered}$$

以上就是所谓的全概率公式。

我们一般见到的数学表示形式如下：

$P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...+P(A_n)P(B|A_n)={\sum }_{i=1}^{n}P(A_i)P(B|A_i)$

贝叶斯公式

现在，坏果作为促销商品，那么顾客想从坏果中选到西瓜的概率是多少，也就是计算 $P(A_1|B)$

**注意：**这里需要区分 $P(A_1|B)$ 和 $P(B|A_1)$ 二者的区别

$P(B|A_1)$ 指的是选西瓜这件事已经确定的情况下，从中选坏果的概率，用图表示

$P(A_1|B)$ 指的是在坏果已经确定的情况下，从中选西瓜的概率，用图表示

根据上图，很容易得到坏果总共有 17 个，其中 10 个西瓜：

$P(A_1|B)=\frac{10}{17}$

用符号代替：

$P(A_1|B)=\frac{P(A_1,B)}{P(B)}=\frac{P(A_1)P(B|A_1)}{P(B)}$

根据联合概率公式：

关于为什么要使用联合概率公式转换，参考上一小节

$P(A_1|B)=\frac{P(A,B)}{P(B)}=\frac{P(A_1)P(B|A_1)}{P(B)}$

根据全概率公式：

$P(A_1|B)=\frac{P(A_1)P(B|A_1)}{P(B)}=\frac{P(A_1)P(B|A_1)}{P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)P(B|A_3)}$

这个就是所谓的贝叶斯公式。

代入值

$P(A_1|B)=\frac{0.5\times 0.2}{0.3\times 0.1+0.5\times 0.2+0.2\times 0.2}=\frac{1}{0.17}=\frac{10}{17}$