题目链接

Leetcode.126 单词接龙 II

题目描述

按字典 wordList完成从单词 beginWord到单词 endWord转化，一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> ... -> sk这样的单词序列，并满足：

每对相邻的单词之间仅有单个字母不同。

转换过程中的每个单词 $s_i（1<=i<=k）$必须是字典 wordList 中的单词。注意，beginWord不必是字典 wordList中的单词。
$s_k==endWord$

给你两个单词 beginWord和 endWord，以及一个字典 wordList。请你找出并返回所有从 beginWord到 endWord 的 最短转换序列 ，如果不存在这样的转换序列，返回一个空列表。每个序列都应该以单词列表 $[beginWord,s_1,s_2,...,s_k]$ 的形式返回。

示例 1：

输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出：[[“hit”,“hot”,“dot”,“dog”,“cog”],[“hit”,“hot”,“lot”,“log”,“cog”]]
解释：存在 2 种最短的转换序列：
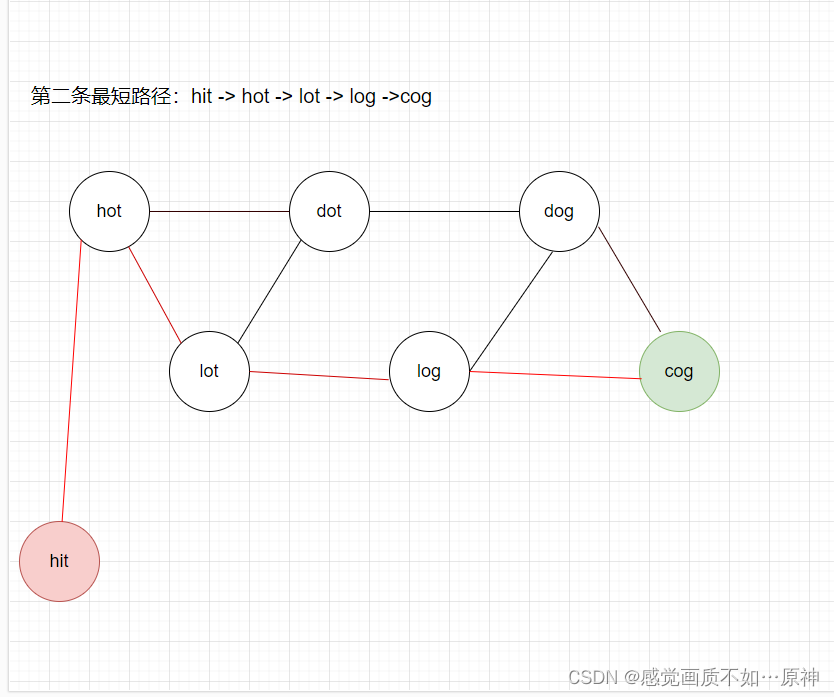
“hit” -> “hot” -> “dot” -> “dog” -> “cog”
“hit” -> “hot” -> “lot” -> “log” -> “cog”

示例 2：

输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
输出：[]
解释：endWord “cog” 不在字典 wordList 中，所以不存在符合要求的转换序列。

提示：

• $1<=beginWord.length<=5$
• $endWord.length==beginWord.length$
• $1<=wordList.length<=500$
• $wordList[i].length==beginWord.length$
• $beginWord、endWord和wordList[i]$ 由小写英文字母组成
• $beginWord!=endWord$
• $wordList$ 中的所有单词 互不相同

分析：

本题在 127. 单词接龙 的基础之上，还要记录最短的路径，求所有的最短路径。

一般这种 求一些路径 我们可以使用 回溯 来解决。

如图，我们要求 起点hit 和 终点cog 的最短路径。

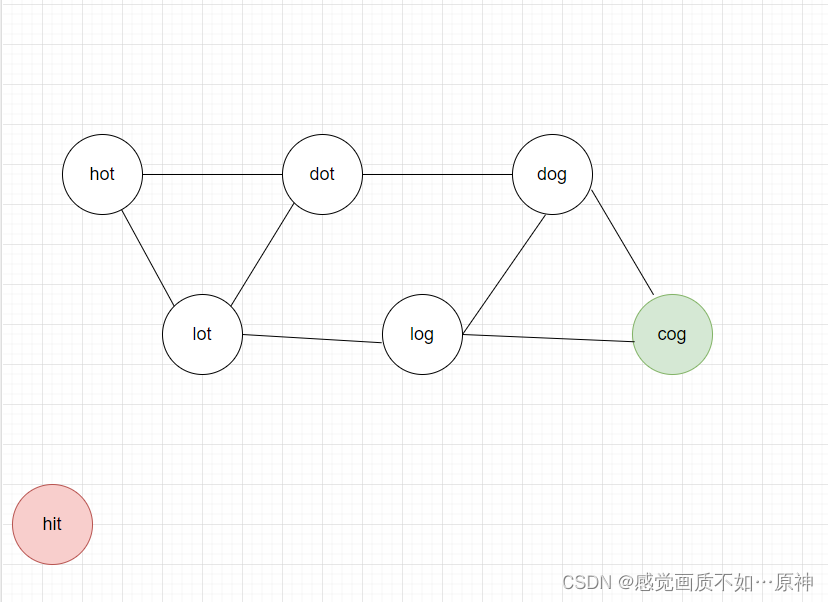
思路：

• 先用一个哈希表 uset 记录所有的单词
• 用一个列表 path 记录路径，合法的 在uset中的单词 才插入到path中。
• 如果遍历到的 当前字符串 $cur==endWord$，说明找到了终点。根据情况将 path 加入到结果列表 res 中：
• • 如果此时的 path.size() < min_d(初始化为无穷大，用来记录最短路径的长度的)，说明又找到了一条更短的路径，所以之前记录在 res 中的路径全部清空，再加入path 同时 min_d 更新为 path.size()。
• • 如果此时的 path.size() == min_d，说明又找到一条相同长度的最短路径，此时将path 直接加入 res即可。

代码：

class Solution {
public:
    //记录 wordList 中的单词
    unordered_set<string> uset;
    //记录结果路径
    vector<vector<string>> res;
    //最短路径长度
    int min_d = 1e9;

    void dfs(string cur,string endWord,vector<string>& path,unordered_set<string>& visited){

        if(cur == endWord){
            int len = path.size();
            if(len < min_d){
                min_d = len;
                res.clear();
                res.push_back(path);
            }
            else if(len == min_d) res.push_back(path);

            return ;
        }

        //此时path.size() > min_d，说明此时的path中肯定不是最短路径 直接返回即可
        if(path.size() > min_d) return ;


        int n = cur.size();
        //从 cur 的每一个位置，都从 'a' 到 'z' 枚举
        for(int i = 0;i < n;i++){
            char op = cur[i];
            for(char c = 'a';c <= 'z';c++){
                //如果 c 与 原字符 op 一样 直接跳过本次循环
                if(op == c) continue;

                cur[i] = c;

                if(uset.count(cur)){
                    //如果已经访问过这个点 也直接跳过本次循环
                    if(visited.count(cur)) continue;
                    
                    //记录新的点
                    visited.insert(cur);
                    path.push_back(cur);

                    dfs(cur,endWord,path,visited);

                    //回溯 恢复现场
                    visited.erase(cur);
                    path.pop_back();
                }
            }
            cur[i] = op;
        }

    }

    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
        unordered_set<string> visited;
        vector<string> path;

        for(auto &s:wordList) uset.insert(s);

        //如果 wordList 不包含 endWord 直接返回空列表
        if(!uset.count(endWord)) return res;

        //path 此时先加入起点
        path.push_back(beginWord);
        //因为是无向图 所以用一个哈希表来记录 已经访问过的点
        visited.insert(beginWord);

        dfs(beginWord,endWord,path,visited);


        return res;
    }
};

但是这份代码会超时。。。

解法二：

• 我们可以先通过 BFS，建出一个最短路径的反向图（因为本质上我们是在求 图的最短路问题，而且因为反向图比较好建）。

建好的图应该是以下这个样子：

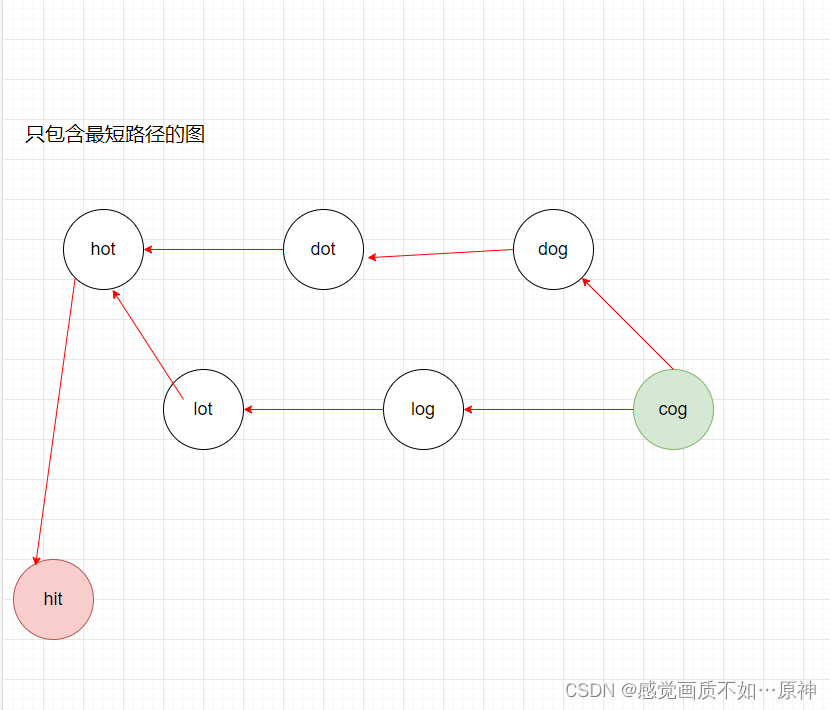
• 所以我们第二步只需要从终点到起点 DFS 即可。

代码：

class Solution {
public:
   //记录结果
    vector<vector<string>> res;
    //图
    unordered_map<string,vector<string>> g;
    vector<string> path;
    string t;


    void dfs(string u){
        if(u == t){
           //因为从终点到起点 所以我们要逆序加入结果列表
            res.emplace_back(path.rbegin(),path.rend());
            return;
        }

        for(auto &v:g[u]){
            path.push_back(v);
            dfs(v);
            //回溯 恢复现场
            path.pop_back();
        }
    }

    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
        //记录从起点开始的长度
        unordered_map<string,int> dist;
        //记录 wordList 的单词
        unordered_set<string> uset(wordList.begin(),wordList.end());
        queue<string> q;

        //起点距离为0
        dist[beginWord] = 0;
        q.push(beginWord);

        while(!q.empty()){
            auto cur = q.front();
            q.pop();

            auto next_str = cur;
            int n = cur.size();


            for(int i = 0;i < n;i++){
                char op = next_str[i];
                for(char c = 'a';c <= 'z';c++){
                    if(c == op) continue;
                    next_str[i] = c;
                    if((uset.count(next_str)) && (!dist.count(next_str) || dist[next_str] == dist[cur] + 1)){
                        //建反向边
                        g[next_str].push_back(cur);
                    }
                    //点 s 是没有访问过的点
                    if(uset.count(next_str) && !dist.count(next_str)){
                        dist[next_str] = dist[cur] + 1;
                        //如果 next_str 是终点，直接跳出循环
                        if(next_str == endWord) break;
                        q.push(next_str);
                    }
                }
                next_str[i] = op;
            }
        }


        //判断从起点能否到达终点 不能直接返回空列表
        if(!dist.count(endWord)) return res;

        //path 加入终点 倒着 dfs
        path.push_back(endWord);
        

        t = beginWord;

        dfs(endWord);

        return res;
    }
};