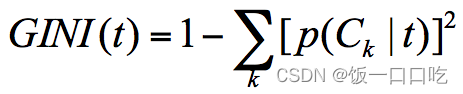本文主要对Python版本PathPlanning运动规划库中RotationToWorldFrame函数的内部计算过程分析,包括相关必备python基础和计算过程分析两部分,并给出了等效的MATLAB版本计算过程程序,方便分析对比。
(注:RotationToWorldFrame函数内部应用的SVD分解(奇异值分解)求旋转矩阵的原理,本文并不进行介绍,在本文最后给出了相关资料,本文仅分析其计算过程)
一、相关Python基础
1、python中的行向量、列向量、矩阵,示例程序如下:
import numpy as np
# 行向量示例
a1=np.array([[1,2,3]])
# 列向量示例
a2=np.array([[40],[50],[60]])
# 矩阵示例
a3=np.array([[1,2,3],[40,50,60]])
print(np.shape(a1))
print(np.shape(a2))
print(np.shape(a3))
运行结果,即例子中a1、a2和a3的维数如下:
(1, 3)
(3, 1)
(2, 3)
2 、@可用于矩阵乘法,.T表示对矩阵进行转置转置,示例程序如下:
e1 = np.array([[1.0] , [2.0] ,[3.0]])
e2 = np.array([[100.0] , [200.0] ,[300.0]])
# @表示矩阵乘法,.T表示转置
c=e1 @ e2.T
print(e1)
print(e2)
print(c)
运行结果如下:
[[1.]
[2.]
[3.]]
[[100.]
[200.]
[300.]]
[[100. 200. 300.]
[200. 400. 600.]
[300. 600. 900.]]
3 、奇异值分解函数SVD
python中的奇异值分解函数如下所示,奇异值分解的相关知识在矩阵论中有介绍,这里不进行解释。
np.linalg.svd(a, full_matrices=True, compute_uv=True)
其中:
(1) a : 是一个形如(M,N)矩阵
(2)full_matrices:的取值是为0或者1,默认值为1,此时u的大小为(M,M),v的大小为(N,N) 。否则u的大小为(M,K),v的大小为(K,N) ,K=min(M,N)。
(3)compute_uv:取值是为0或者1,默认值为1,表示计算u,s,v。为0的时候只计算s。
4、python中可以用det()函数求取矩阵求行列式(标量),如下所示,其中a是要求行列式的矩阵
np.linalg.det(a)
5、python中可以用 np.diag(a)来构建对角矩阵 中,当a是一个1维数组/向量时, np.diag(a)输出一个以一维数组为对角线元素的矩阵,当a是一个二维矩阵时, np.diag(a)输出该矩阵的对角线元素。
np.linalg.det(a)
二、RotationToWorldFrame函数内部计算过程分析
PathPlanning运动规划库中给出的RotationToWorldFrame函数程序如下所示:
# RotationToWorldFrame函数用于旋转到世界坐标系
def RotationToWorldFrame(x_start, x_goal, L):
a1 = np.array([[(x_goal.x - x_start.x) / L], # numpy.array用于创建一个数组
[(x_goal.y - x_start.y) / L], [0.0]])
e1 = np.array([[1.0], [0.0], [0.0]])
M = a1 @ e1.T
U, _, V_T = np.linalg.svd(M, True, True)
C = U @ np.diag([1.0, 1.0, np.linalg.det(U) * np.linalg.det(V_T.T)]) @ V_T
return C
其实,以上函数的运用了SVD分解(奇异值分解)求旋转矩阵的方法,本文对该方法的原理不进行介绍,仅分析其计算过程。
为方便对以上程序进行分析,我绘制了以下简图

结合以上图示容易看出,上面程序中的(x_goal.x - x_start.x) / L即为cos(a),(x_goal.y - x_start.y) / L即为sin(a),因此,容易求得M的取值如下所示:
[cos(a), 0, 0]
[sin(a), 0, 0]
[ 0, 0, 0]
当a取π/4时,M的取值如下:
0.7070 0 0
0.7070 0 0
0 0 0
此时,使用svd函数进行奇异值分解得到的U、 S 、V_T,如下所示:
U =
-0.7071 0 -0.7071
-0.7071 0 0.7071
0 1.0000 0
S =
0.9998 0 0
0 0 0
0 0 0
V_T =
-1 0 0
0 0 1
0 1 0
此时,容易得到det(U)和det(V)的值均为1,从而此时:
np.diag([1.0, 1.0, np.linalg.det(U) * np.linalg.det(V_T.T)])
=
1.0000 0 0
0 1.0000 0
0 0 1.0000
C = U @ np.diag([1.0, 1.0, np.linalg.det(U) * np.linalg.det(V_T.T)]) @ V_T
=
0.7071 -0.7071 0
0.7071 0.7071 0
0 0 1.0000
接下来,我们用MATLAB来复现一下以上RotationToWorldFrame(x_start, x_goal, L)函数的计算过程,程序如下,并设旋转角度a=π/6
% 设定选择角度a
a=pi/6;
b=[cos(a); sin(a); 0];
c=[1 0 0];
M=b*c
[U, S ,V_T]=svd(M)
V=V_T';
N=diag([1.0, 1.0, det(U) * det(V)])
C=U*N*V
% 绕Z轴旋转a度的坐标旋转矩阵计算结果
C2=[cos(a),-sin(a),0;sin(a),cos(a),0;0,0,1]
通过以上程序,我们在MATLAB的实时脚本中可以很方便的得到各个变量的值,如下图所示:
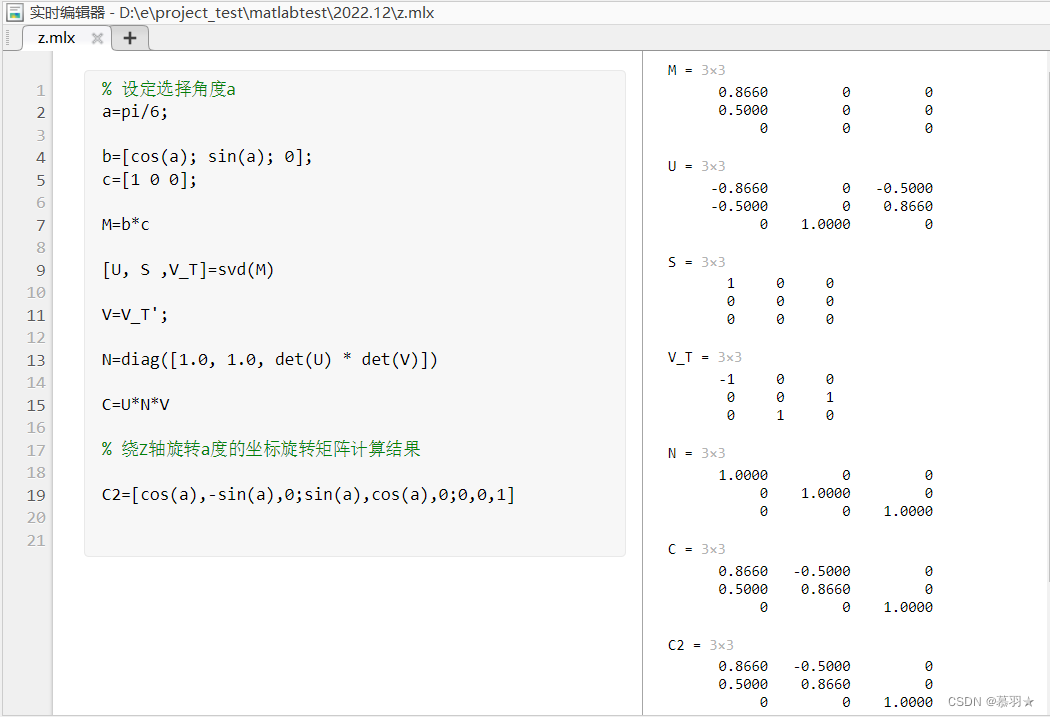
因此,容易得出,以上函数的计算结果C,通过机器人学当中介绍的三维空间下绕z轴旋转a度的坐标旋转矩阵也可以得到,如下图所示(下图标的为旋转θ度的情况)

所以,看起来好像直接用三维空间下绕z轴旋转a度的坐标旋转矩阵计算,就可以得到跟RotationToWorldFrame函数经过复杂且不容易理解的内部计算相同的计算结果。
最后,放一下SVD分解(奇异值分解)求旋转矩阵原理介绍的一些资料,有兴趣的可以去看一下
1、相关论文 Least-Squares Rigid Motion Using SVD【点击可跳转】
2、上述论文的相关笔记 SVD求解旋转矩阵【点击可跳转】
3、相关博客 SVD计算旋转,平移矩阵【点击可跳转】