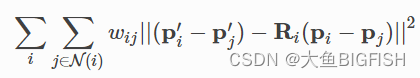一 Prometheus监控介绍

1.微服务监控系统promethues介绍

• 是一套开源的监控&报警&时间序列数据库的组合

• 基本原理是通过HTTP协议周期性抓取被监控组件的状态

• 适合Docker、 Kubernetes环境的监控系统

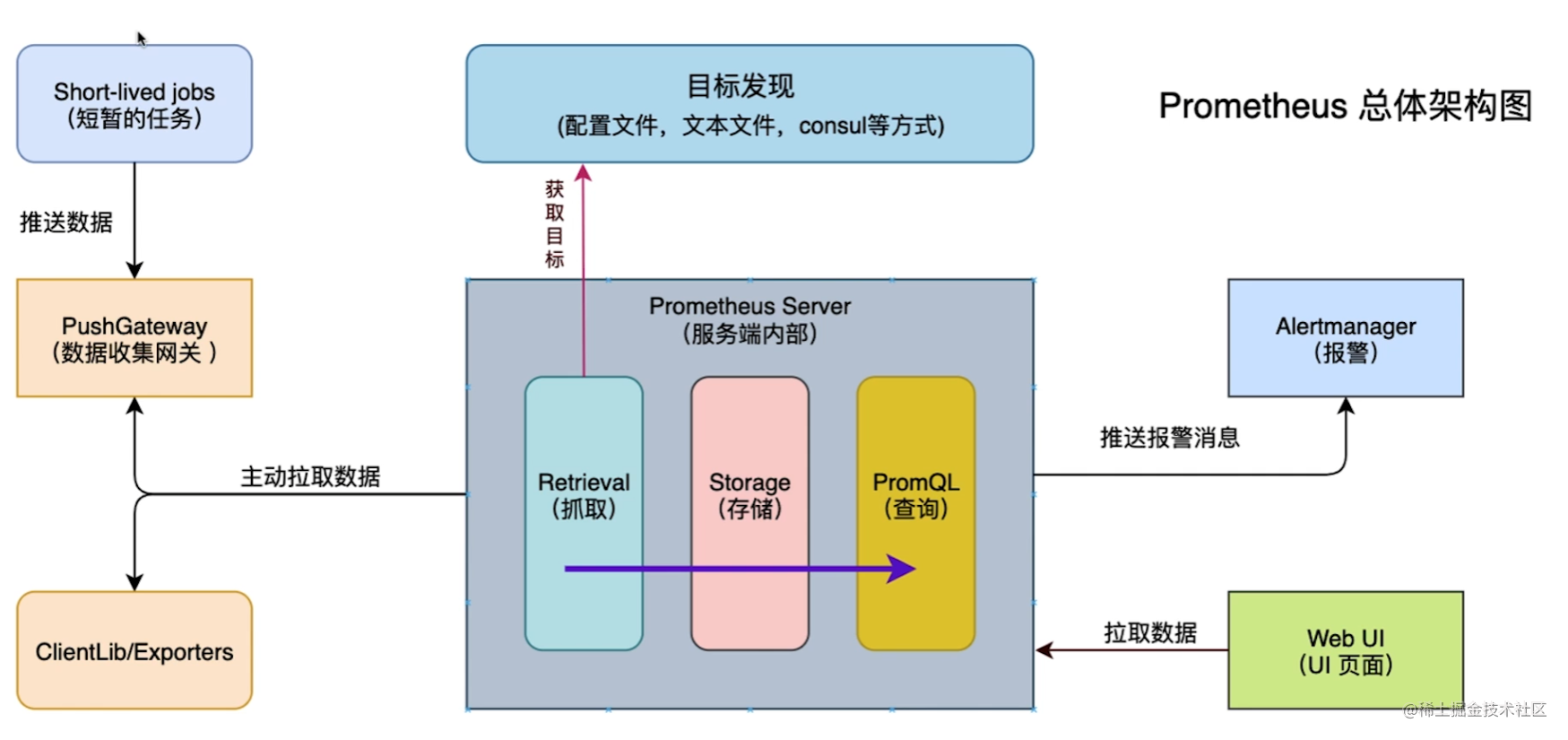
2.微服务监控系统promethues工作流程

• Prometheus server定期从配置好的jobs/exporters/Pushgateway中拉数据

• Prometheus server记录数据并且根据报警规则推送alert数据

• Alertmanager 根据配置文件,对接收到的警报进行处理,发出告警。

• 在图形界面中,可视化采集数据

二 Prometheus监控重要组件和重要概念

1.微服务监控系统promethues重要组件

1. Prometheus Server:用于收集和存储时间序列数据。

2. Client Library:客户端库成相应的metrics并暴露给Prometheus server

3. Push Gateway:主要用于短期的jobs

4. Exporters: 用于暴露已有的第三方服务的metrics给Prometheus

5. Alertmanager: 从Prometheus server端接收到alerts后,会进行

2.微服务监控系统promethues重要概念

1. Prometheus 中存储的数据为时间序列

2. 格式上由metric的名字和一系列的标签(键值对)唯一标识组成

3. 不同的标签则代表不同的时间序列

4. Counter 类型: - -种累加的指标,如:请求的个数，出现的错误数等

5. Gauge 类型:可以任意加减,如:温度,运行的goroutines的个数

6. Histogram 类型:可以对观察结果采样,分组及统计,如:柱状图

7. Summary 类型:提供观测值的count和sum功能,如:请求持续时间

8. instance : -个单独监控的目标，一般对应于一 个进程。

9. jobs:一组同种类型的instances (主要用于保证可扩展性和可靠性)

三 微服务监控系统grafana看板

• 拥有 丰富dashboard和图表编辑的指标分析平台

• 拥有自己的权限管理和用户管理系统

• Grafana 更适合用于数据可视化展示

四 Prometheus监控+Grafana看板安装

1.安装Prometheus监控

• 拉取镜像：

docker pull bitnami/prometheus

• 运行：

docker run -d -p 9090:9090 bitnami/prometheus

• 查看是否运行：

docker ps

• 图形化界面：
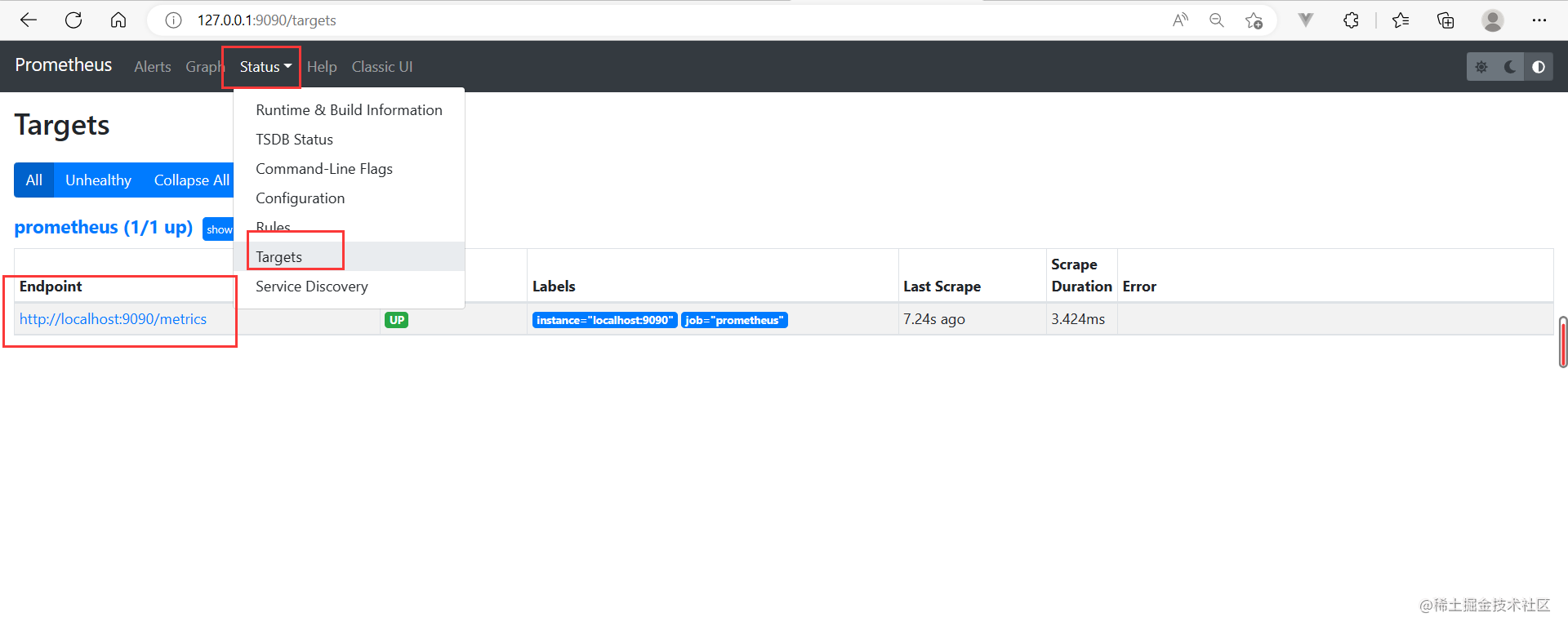
  • 浏览器访问 http://127.0.0.1:9090/

2.安装Grafana看板

• 拉取镜像：

docker pull grafana/grafana

• 运行：

docker run -d -p 3000:3000 grafana/grafana

• 查看是否运行：

docker ps

• 图形化界面：
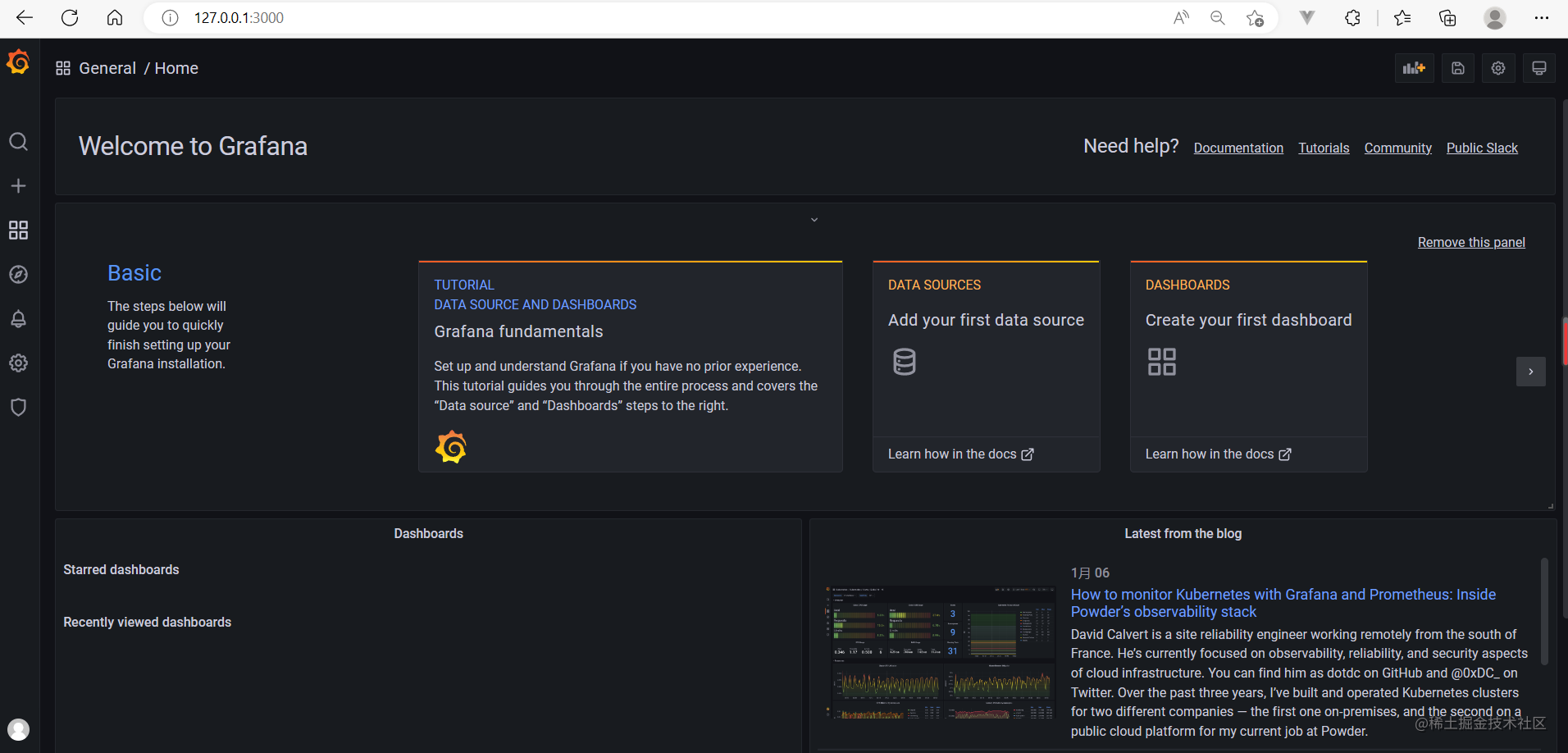
  • 浏览器访问 http://127.0.0.1:3000/

五 Prometheus监控使用

• 在micro目录下新建prometheus.go文件

go get github.com/prometheus/client_golang/prometheus/promhttp

• 编写以下代码：

package micro

import (
   "github.com/prometheus/client_golang/prometheus/promhttp"
   "log"
   "net/http"
   "strconv"
)

func PrometheusBoot(host string,port int){
   http.Handle("/metrics",promhttp.Handler())
   //启动web服务
   go func() {
      err := http.ListenAndServe(host+":"+strconv.Itoa(port),nil)
      if err!= nil{
         log.Fatal(("监控启动失败"))
      }
      log.Fatal("监控启动,端口为: "+strconv.Itoa(port))
   }()
}

六 Prometheus监控注册服务

• 导包：

go get github.com/micro/go-plugins/wrapper/monitoring/prometheus/v2

• 在main.go文件中写入以下代码

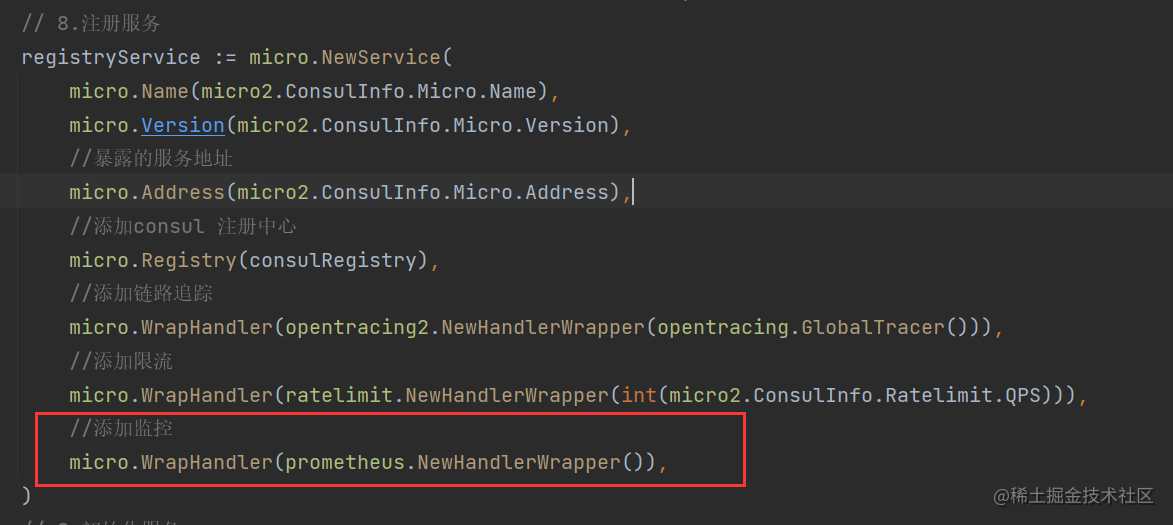
// 7.暴露监控地址
micro2.PrometheusBoot(micro2.ConsulInfo.Prometheus.Host, int(micro2.ConsulInfo.Prometheus.Port))

• 注：传的参数是使用consul导入的，可以换成自定义的

• 注册服务

//添加监控
micro.WrapHandler(prometheus.NewHandlerWrapper()),

七 Prometheus监控图形化界面

• 运行项目

Prometheus原生看板

Grafana看板

• 首次登录，账号：admin；密码：admin

八 最后

• 至此，go-micro微服务Prometheus监控工作就正式完成。

• 接下来就开始微服务ELK介绍的代码编写了，希望大家关注博主和关注专栏，第一时间获取最新内容，每篇博客都干货满满。

欢迎大家加入 夏沫の梦的学习交流 进行学习交流经验，点击