数据规模->时间复杂度

<=10^4 😮(n^2)
<=10^7:o(nlogn)
<=10^8:o(n)
10^8<=:o(logn),o(1)

内容

二维数组中的路径问题
买卖股票的最佳时机

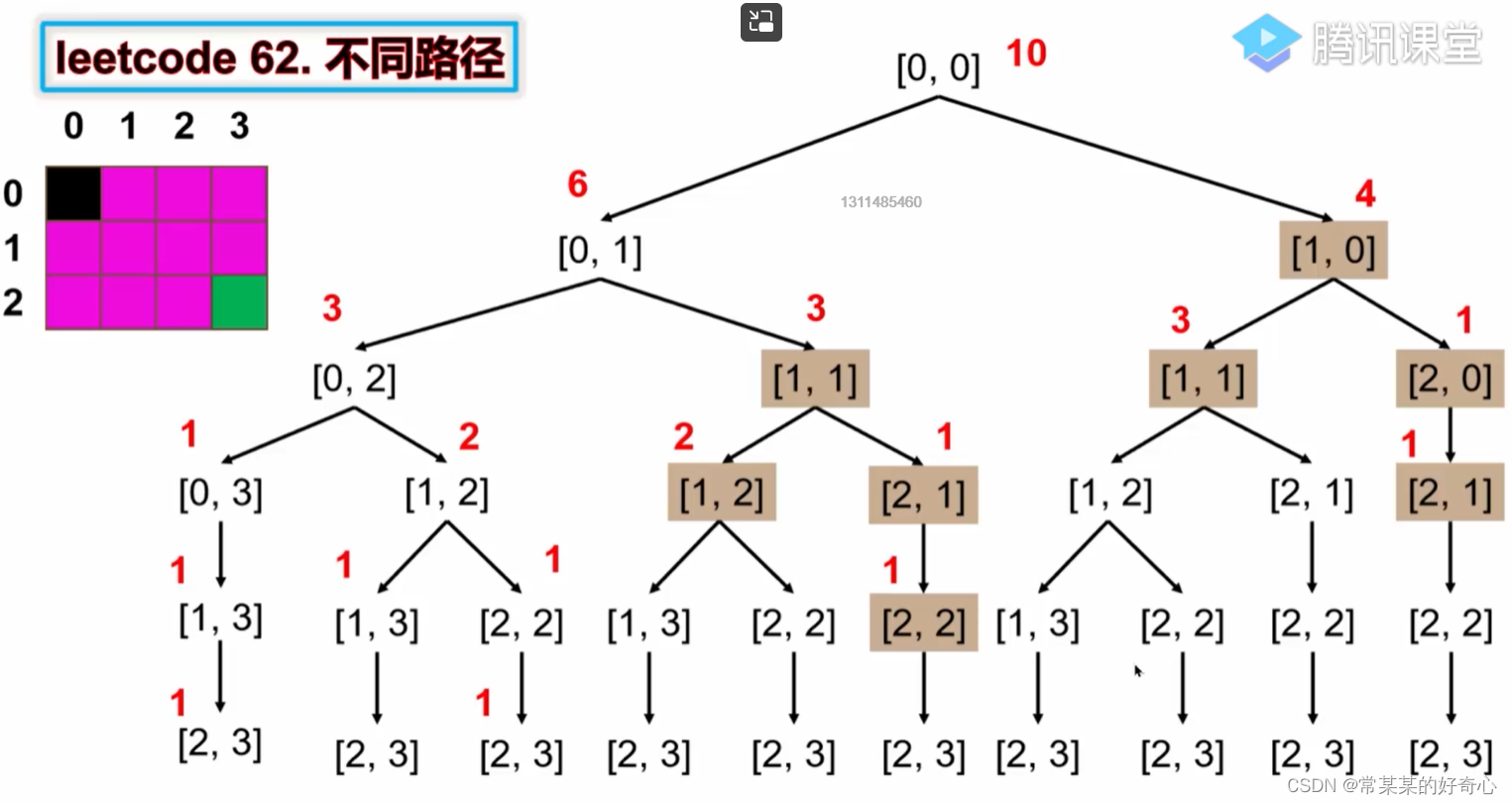
lc 62【剑指 098】【top100】：不同路径
https://leetcode.cn/problems/unique-paths/
提示：
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

#方案一：dfs+记忆化
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        memo=[[-1]*n for _ in range(m)]
        def dfs(i,j):
            if i==m-1 and j==n-1:return 1
            if i>=m or j>=n:return 0
            if memo[i][j]!=-1:return memo[i][j]
            #
            memo[i][j]=dfs(i+1,j)+dfs(i,j+1)
            return memo[i][j] #后序
        return dfs(0,0)

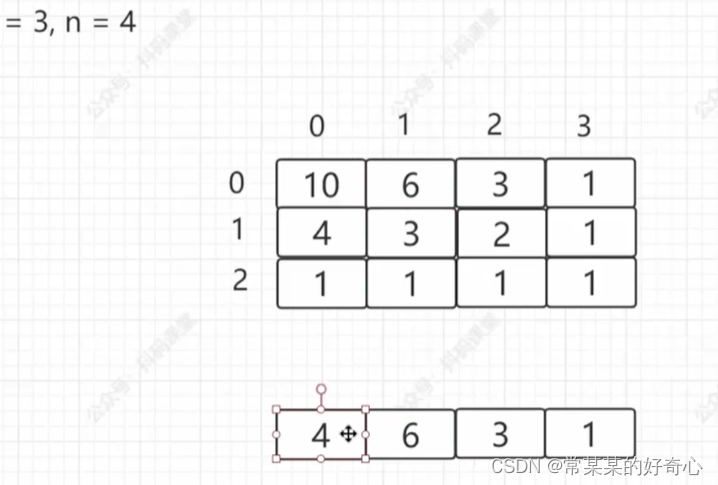
#方案二：dp(自底而上，左上至右下路径数更新)+压缩
class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp=[[0]*n for _ in range(m)] #[i][j]到[m-1][n-1]的路径数
        for i in range(m-1,-1,-1):
            for j in range(n-1,-1,-1):
                if i==m-1 or j==n-1:dp[i][j]=1 #最后一行/一列
                else:dp[i][j]=dp[i+1][j]+dp[i][j+1]
        return dp[0][0]

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp=[0]*n 
        for i in range(m-1,-1,-1):
            for j in range(n-1,-1,-1):
                if j==n-1:dp[j]=1 #最后一行/一列
                else:dp[j]=dp[j]+dp[j+1]
        return dp[0]
        
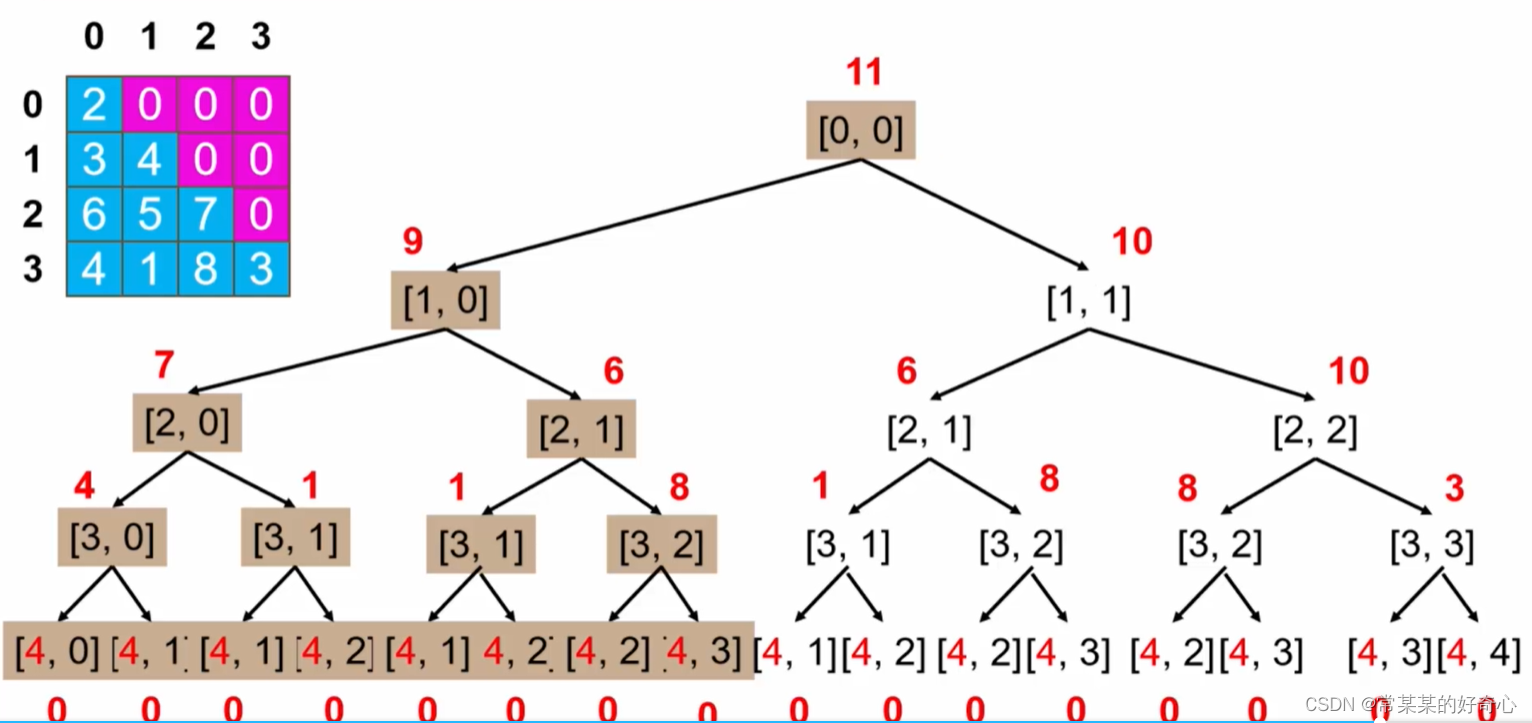
#方案三：dp(自上而下，右下至左上路径数更新)

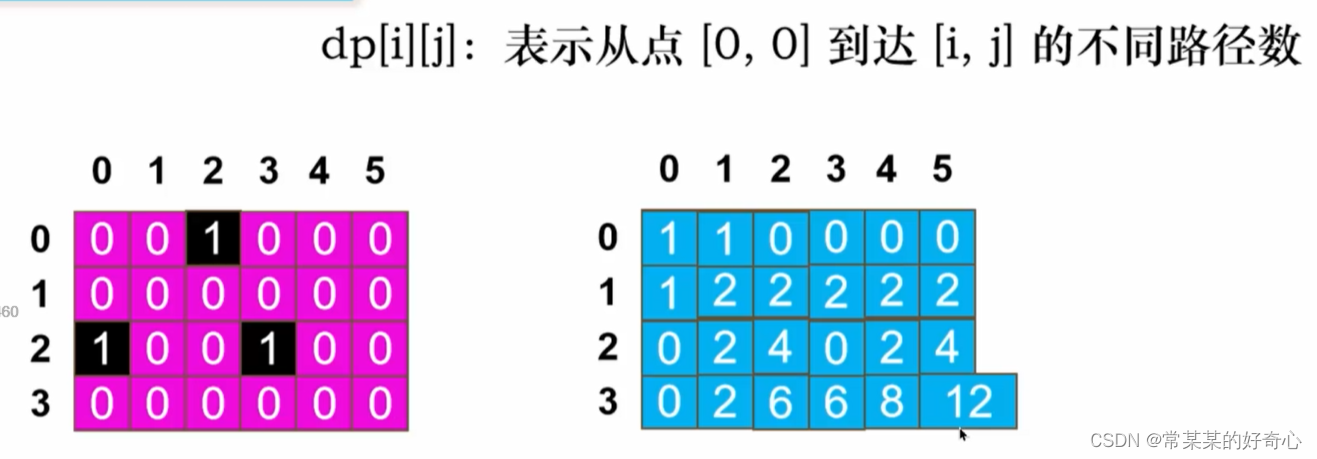
lc 63 ：不同路径 II
https://leetcode.cn/problems/unique-paths-ii/
提示：
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

#方案一：dp
class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m,n=len(obstacleGrid),len(obstacleGrid[0])
        dp=[[0]*n for _ in range(m)]
        #
        if obstacleGrid[0][0]==0:dp[0][0]=1
        for i in range(m):
            if dp[i-1][0]==1 and obstacleGrid[i][0]==0:dp[i][0]=1    
        for j in range(n):
            if dp[0][j-1]==1 and obstacleGrid[0][j]==0:dp[0][j]=1
        #
        for i in range(1,m):#key:1
            for j in range(1,n):
                if obstacleGrid[i][j]==1:continue
                dp[i][j]=dp[i-1][j]+dp[i][j-1]
        #
        return dp[m-1][n-1]
class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m,n=len(obstacleGrid),len(obstacleGrid[0])
        dp=[[0]*n for _ in range(m)]
        #
        for i in range(m):#key:1
            for j in range(n):
                if obstacleGrid[i][j]==1:continue
                
                if i==0 and j==0:dp[i][j]=1
                elif j==0:#此时obstacleGrid[i][j]==0
                    dp[i][j]=dp[i-1][j]
                elif i==0:
                    dp[i][j]=dp[i][j-1]
                else:
                    dp[i][j]=dp[i-1][j]+dp[i][j-1]
        #
        return dp[m-1][n-1]

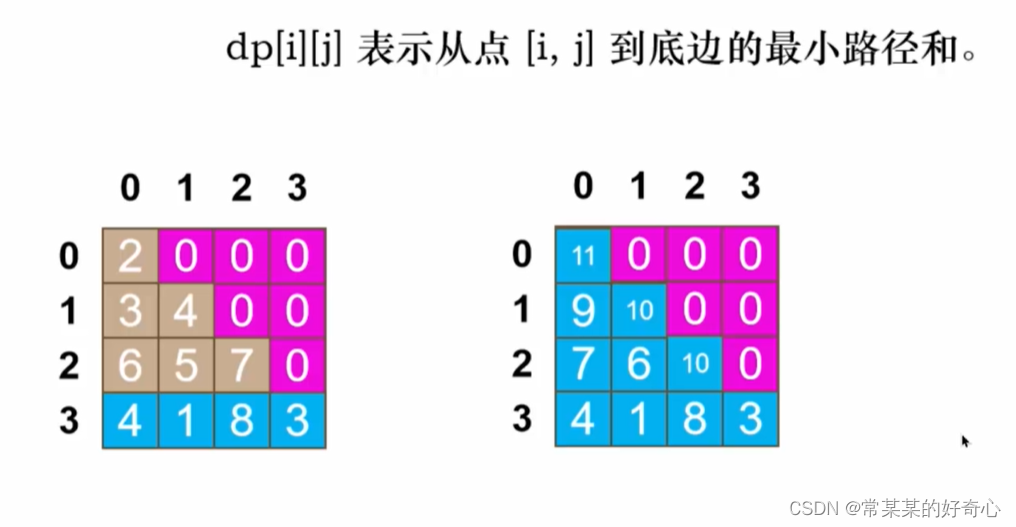
lc 120【剑指 100】：三角形最小路径和
https://leetcode.cn/problems/triangle/
提示：
1 <= triangle.length <= 200
triangle[0].length == 1
triangle[i].length == triangle[i - 1].length + 1
-10^4 <= triangle[i][j] <= 10^4
进阶：
你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题吗？

#方案一：dfs
class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        m=len(triangle) #注意：len(triangle[0])=1
        memo=[[float('inf')]*m for _ in range(m)]
        #
        def dfs(i,j):
            if i==m or j==m:return 0
            if memo[i][j]!=float('inf'):return memo[i][j]
            #
            memo[i][j]=min(dfs(i+1,j),dfs(i+1,j+1))+triangle[i][j]
            return memo[i][j]
        return dfs(0,0)
#方案二：dp
class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        m=len(triangle) #注意：len(triangle[0])=1
        dp=[[float('inf')]*m for _ in range(m)]
        #
        for j in range(m):
            dp[m-1][j]=triangle[m-1][j]
        
        for i in range(m-2,-1,-1):
            for j in range(i+1):
                dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j]
      
        return dp[0][0]
        
#方案三：dp+压缩
class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        m=len(triangle) #注意：len(triangle[0])=1
        dp=[float('inf')]*m 
        #
        for j in range(m):
            dp[j]=triangle[m-1][j]
        
        for i in range(m-2,-1,-1):
            for j in range(i+1):
                dp[j]=min(dp[j],dp[j+1])+triangle[i][j]
      
        return dp[0]

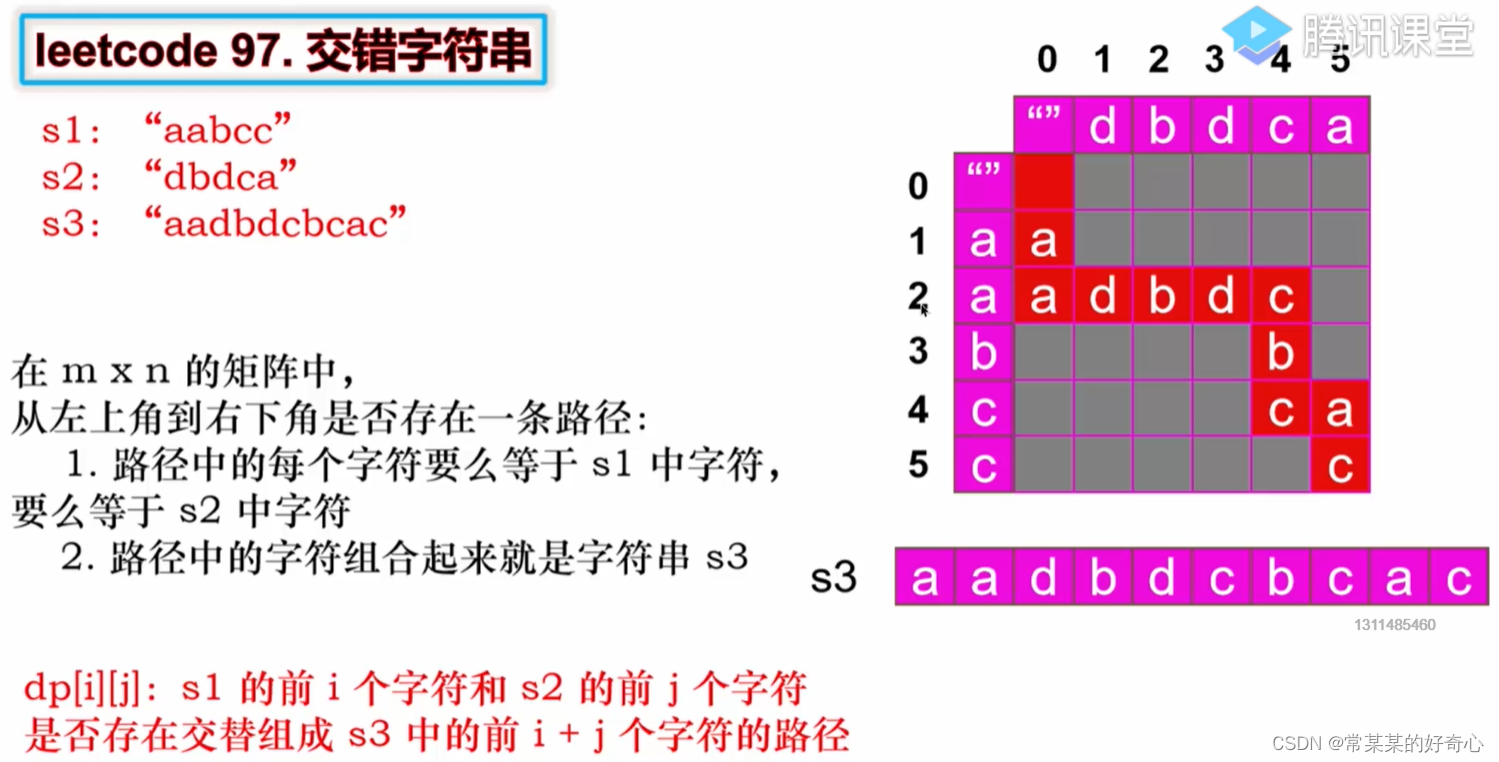
lc 97【剑指 096】：交错字符串
https://leetcode.cn/problems/interleaving-string/
注意：a + b 意味着字符串 a 和 b 连接。
提示：
0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1、s2、和 s3 都由小写英文字母组成
进阶：
您能否仅使用 O(s2.length) 额外的内存空间来解决它?

#dp
class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m,n,t=len(s1),len(s2),len(s3)
        if m+n != t:return False
        dp=[[False]*(n+1) for _ in range(m+1)]
        dp[0][0]=True
        #
        for i in range(1,m+1):
            if s1[i-1]==s3[i-1]:
                dp[i][0]=True #注意dp的i对应字符位置i-1
            else:break
        for j in range(1,n+1):
            if s2[j-1]==s3[j-1]:
                dp[0][j]=True
            else:break
        #
        for i in range(1,m+1):
            for j in range(1,n+1):
                k=i+j
                s1_s3=s1[i-1]==s3[k-1] and dp[i-1][j]#s1第i个字符、前i-1字符的匹配情况
                s2_s3=s2[j-1]==s3[k-1] and dp[i][j-1]
                dp[i][j]=s1_s3 or s2_s3 #考虑两种方向
        #
        return dp[m][n]

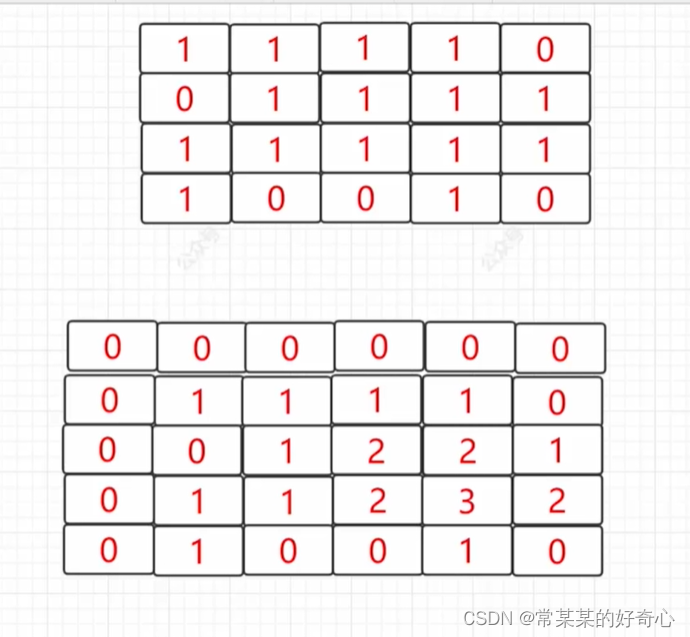
lc 221【top100】：最大正方形
https://leetcode.cn/problems/maximal-square/
提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 ‘0’ 或 ‘1’

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m,n=len(matrix),len(matrix[0])
        #
        dp=[[0]*(n+1) for _ in range(m+1)]#key:有利于统一化

        max_len=0
        # for i in range(m):
        #     if matrix[i][0]=='1':
        #         dp[i][0]=1
        #         max_len=max(max_len,dp[i][0])
        # for j in range(n):
        #     if matrix[0][j]=='1':
        #         dp[0][j]=1
        #         max_len=max(max_len,dp[0][j])

        for i in range(1,m+1):
            for j in range(1,n+1):
                if matrix[i-1][j-1]=='1':
                    dp[i][j]=min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j]))+1 #key
                    max_len=max(max_len,dp[i][j])
        return max_len**2

系列算法题：买卖股票的最佳时机

lc 121【剑指 63】【top100】：买卖股票的最佳时机
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/
提示：
1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4

# k=1->省去一维[k]
#方案一：dp
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        m=len(prices)
        
        dp=[[0]*2 for _ in range(m)]
        dp[0][0],dp[0][1]=0,-prices[0]

        for i in range(1,m):
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i])
            dp[i][1]=max(dp[i-1][1],0-prices[i])
        
        return dp[m-1][0]
#方案二：dp+压缩
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        m=len(prices)
        
        dp=[0]*2 #或者用两个变量
        dp[0],dp[1]=0,-prices[0]

        for i in range(1,m):
            dp[0]=max(dp[0],dp[1]+prices[i])
            dp[1]=max(dp[1],0-prices[i])
        
        return dp[0]

lc 122 ：买卖股票的最佳时机 II
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/
提示：
1 <= prices.length <= 3 * 10^4
0 <= prices[i] <= 10^4

#k=无穷，k-1=无穷->省去一维[k]
#dp
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        m=len(prices)
        
        dp=[[0]*2 for _ in range(m)]
        dp[0][0],dp[0][1]=0,-prices[0]

        for i in range(1,m):
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i])
            dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i])#key
        
        return dp[m-1][0]
#dp+压缩 
##也可以变成两个变量

lc 123 ：买卖股票的最佳时机 III
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
提示：
1 <= prices.length <= 10^5
0 <= prices[i] <= 10^5

#<=2:2,1((从 1 开始)，第 0 次交易的话，利润肯定是0)
#dp
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n=len(prices)
        
        dp=[[[0]*2 for _ in range(3)] for _ in range(n)]
        dp[0][1][0]=dp[0][2][0]=0
        dp[0][1][1]=dp[0][2][1]=-prices[0]

        for i in range(1,n):
            dp[i][1][0]=max(dp[i-1][1][0],dp[i-1][1][1]+prices[i])
            dp[i][1][1]=max(dp[i-1][1][1],dp[i-1][0][0]-prices[i])
            dp[i][2][0]=max(dp[i-1][2][0],dp[i-1][2][1]+prices[i])
            dp[i][2][1]=max(dp[i-1][2][1],dp[i-1][1][0]-prices[i])

        return dp[n-1][2][0]
#dp+压缩
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n=len(prices)
        
        dp=[[0]*2 for _ in range(3)]
        dp[1][0]=dp[2][0]=0 #也可以变成四个变量
        dp[1][1]=dp[2][1]=-prices[0]

        for i in range(1,n):
            dp[1][0]=max(dp[1][0],dp[1][1]+prices[i])
            dp[1][1]=max(dp[1][1],dp[0][0]-prices[i])
            dp[2][0]=max(dp[2][0],dp[2][1]+prices[i])
            dp[2][1]=max(dp[2][1],dp[1][0]-prices[i])

        return dp[2][0]

lc 188 ：买卖股票的最佳时机 IV
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/
注意：
你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
提示：
0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000

#方案一：dp
##<=k:k,k-1,...,1((从 1 开始)，第 0 次交易的话，利润肯定是0)
class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        n=len(prices)
        
        dp=[[[0]*2 for _ in range(k+1)] for _ in range(n)]

        for j in range(1,k+1):
            dp[0][j][0]=0
            dp[0][j][1]=-prices[0]
        
        for i in range(1,n):
            for j in range(1,k+1):
                dp[i][j][0]=max(dp[i-1][j][0], dp[i-1][j][1]+prices[i])
                dp[i][j][1]=max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i])

        return dp[n-1][k][0]
#方案二：dp+优化(贪心)
class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        n=len(prices)

        #这里相当于'无限取'->贪心
        if k>=n//2:
            res=0
            for i in range(1,n):
                if prices[i]>prices[i-1]:
                    res+=prices[i]-prices[i-1]
            return res 
   
        dp=[[[0]*2 for _ in range(k+1)] for _ in range(n)]

        for j in range(1,k+1):
            dp[0][j][0]=0
            dp[0][j][1]=-prices[0]
        
        for i in range(1,n):
            for j in range(1,k+1):
                dp[i][j][0]=max(dp[i-1][j][0], dp[i-1][j][1]+prices[i])
                dp[i][j][1]=max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i])

        return dp[n-1][k][0]
#方案三：dp+压缩
##去除一维

lc 309【top100】：最佳买卖股票时机含冷冻期
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/
注意：
你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
提示：
1 <= prices.length <= 5000
0 <= prices[i] <= 1000

#dp
class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n=len(prices)
        #
        dp=[[0]*2 for _ in range(n)]
        dp[0][0]=0
        dp[0][1]=-prices[0]
        #
        for i in range(1,n):
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i])
            dp[i][1]=max(dp[i-1][1],dp[i-2][0]-prices[i])#i-1天卖出股票后,无法在i天买入股票 (即冷冻期为 1 天)->i-2天卖
        return dp[n-1][0]
#dp+压缩
##去除一维

lc 714 ：买卖股票的最佳时机含手续费
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/
注意：
这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。
提示：
1 <= prices.length <= 5 * 10^4
1 <= prices[i] < 5 * 10^4
0 <= fee < 5 * 10^4

#dp
class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        n=len(prices)
        #
        dp=[[0]*2 for _ in range(n)]
        dp[0][0]=0
        dp[0][1]=-prices[0]-fee#你每笔交易都需要付手续费（这里统一用在买入时）
        #
        for i in range(1,n):
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i])
            dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]-fee)
        return dp[n-1][0]
#dp+压缩
#去除一维/用两个量代替