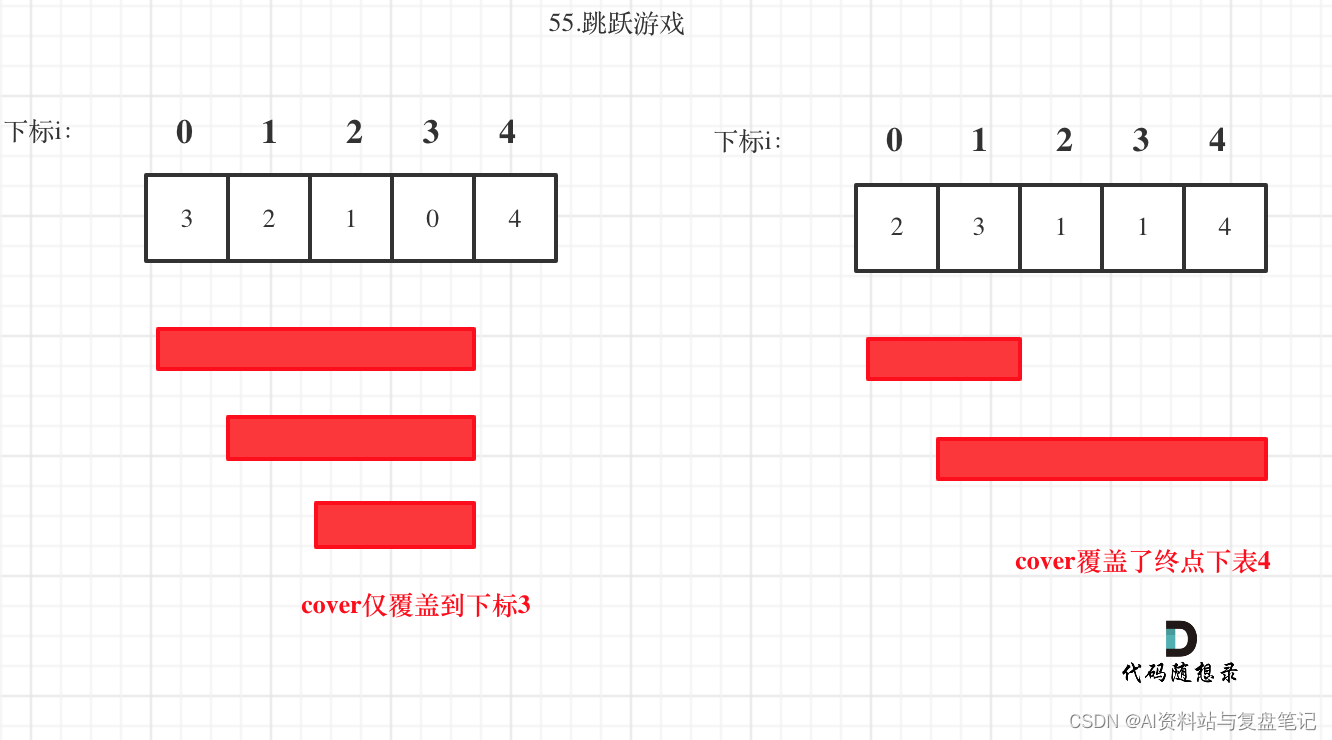
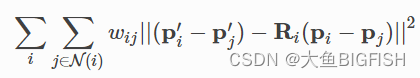题意：1e5长的数组，ai<=1e5，问要将其变成等差数列的最小次数；

分析：

简单分析可得 —— 显然这个答案是固定的，就是原数列本来就能成为等差数列的最大个数。 但是最直接的想法是 的，一维枚举起始位置，一维扫过去，发现暂时没法优化，所以转变思路，看能否换个枚举方式，转而枚举 d（差值），同时发现如果差值大的话，完全不需要枚举完整个数列。

马上想到根号分治，对值域分治，对于大于根号 k 的差值，只需要枚举根号的长度即可，这里的复杂度是 ，但是对于前根号 k 的值，就不知道如何处理了；（我当时还想着是枚举位置，再枚举位置），但实际上，完全可以利用等差公式根据位置推到，也就是对于每个 d ，看 的众数是多少，由于再加个 log 会 T，所以开个桶解决【对于小于根号的处理方式跟这题Problem - C - Codeforces  很像】

Problem - E - Codeforces 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5;
const int mo = 998244353;
#define pb push_back
#define pii pair<int,int>
#define ft first
#define sd second
#define ffor(i,a,b,c) for(int i=(a);i<(b);i+=(c))
#define For(i,a,b,c) for(int i=(a);i<=(b);i+=(c))
#define rfor(i,a,b,c) for(int i=(a);i>(b);i-=(c))
#define Rfor(i,a,b,c) for(int i=(a);i>=(b);i-=(c))
#define all(x) (x).begin(), (x).end()
#define debug1(x) cerr<<"! "<<x<<endl;
#define debug2(x,y) cerr<<"#  "<<x<<" "<<y<<endl;
int tax[N*1000];
class Partition
{
public:
	Partition(int _n) : n(_n) {
		v.resize(n + 1);
		for(int i = 1; i <= n; i++) {
			cin >> v[i];
		}
		blo = 300; //块可以开的比根号稍微小一点,不然桶开不下,因为1GB最大约1e9个int
	}

	int cal() {
		int mx = 0;
		for (int d = 0; d <= blo; d++) {
			for (int i = 1; i <= n; i++) {
				mx = max(mx, ++tax[v[i] - i*d + del]);
			}
			for (int i = 1; i <= n; i++) {
				tax[v[i] - i*d + del] = 0;
			}
		}
		//递增的等差数列,所以只要固定位置往右枚举就行,不需要再考虑左
		for (int i = 1; i <= n; i++) {
			for(int j = i + 1; j <= n && (j - i) * blo <= N; j++) {
				if((v[i] - v[j]) % (i - j) == 0) mx = max(mx, ++tax[(v[i] - v[j]) / (i - j) + N] + 1);
			}
			for(int j = i + 1; j <= n && (j - i) * blo <= N; j++) {
				if((v[i] - v[j]) % (i - j) == 0) tax[(v[i] - v[j]) / (i - j) + N] = 0;
			}
		}

		return n - mx;
	}

	int slv() {
		int ans = cal();
		reverse(v.begin() + 1, v.end());
		ans = min(ans, cal());
		return ans;
	}

private:
	int n, blo;
	vector<int> v;
	const int del = 30000000;
};
void slv() {
	int n; cin >> n;
	Partition Pt(n);
	cout << Pt.slv() << '\n';
}
int main() {
	ios::sync_with_stdio(false); cin.tie(0);
	slv();
}

PS:代码有借鉴别人，当时没想到负的也可以，一直没调出来。

感觉分块目前见到的有对序列分块，对值域分块，对询问分块。 当然每个都可以有他的衍生，而根号分块可能其实就是从属于值域分块