专注系列化、高质量的R语言教程
推文索引 | 联系小编 | 付费合集
本文是年前的最后一篇推文,我们来学习一下使用最小二乘法和最大似然法进行非线性模型估计。
模型估计是指,在模型形式已知的情况下,求解出可以使已有数据与模型形式最大程度上相符合的待定系数的过程。这个过程实际上是一个数学优化过程,不同的估计方法所使用的目标函数不同。
最小二乘法和最大似然法是最常见的两种方法。从表面上看,前者不需要对数据分布做任何假设,而后者需要事先规定数据的分布模式(即概率分布密度)。
本篇目录如下:
1 示例数据
2 最小二乘法
3 最大似然法
1 示例数据
如下示例数据来自An Introduction to R的11.7.1节:
data <- data.frame(
x = c(0.02, 0.02, 0.06, 0.06,
0.11, 0.11, 0.22, 0.22,
0.56, 0.56, 1.10, 1.10),
y = c(76, 47, 97, 107,
123, 139, 159, 152,
191, 201, 207, 200)
)
plot(y ~ x, data = data)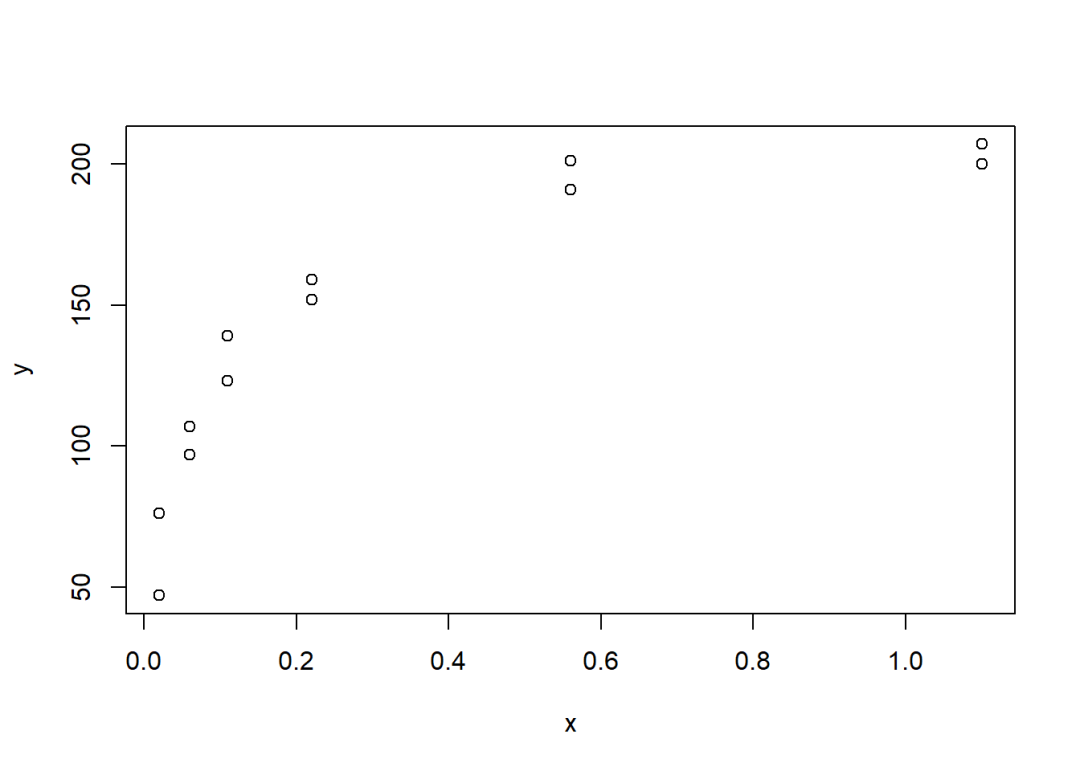
现假设已知和的关系可以通过下式进行拟合:
其中,、为待估计系数。
2 最小二乘法
最小二乘法(Least Square)的原理十分简单,其目标函数和优化方向是使误差平方和(sum of the squared errors, SSE)最小。
则根据最小二乘法,本例的优化目标为:
在R语言中,可以使用基础包stats工具包中的nlm()函数来解决这个问题。它的语法结构如下:
nlm(f, p, ..., hessian = FALSE,
typsize = rep(1, length(p)),
fscale = 1, print.level = 0,
ndigit = 12, gradtol = 1e-6,
stepmax = max(1000 * sqrt(sum((p/typsize)^2)), 1000),
steptol = 1e-6, iterlim = 100,
check.analyticals = TRUE)主要参数如下:
参数
f是目标函数,其中需要估计的系数使用向量p的元素表示;其他参数可自命名;参数
p是待估计系数的初始值;使用向量表示;参数
...表示f中除了p以外的其他参数。
本例中,f参数可以如下进行定义:
f <- function(p, x, y) sum((y - p[1]*x/(x + p[2]))^2)初始值的选取可能会对模型估计有一定的影响。通常情况下,可先根据原始数据进行试验,若拟合出的曲线能大致位于原始数据附近,则可将试验系数作为初始值。
plot(y ~ x, data = data)
p1 = 150; p2 = 0.1
lines(data$x, p1*data$x/(data$x + p2), col = "red")
p1 = 200; p2 = 0.1
lines(data$x, p1*data$x/(data$x + p2), col = "blue")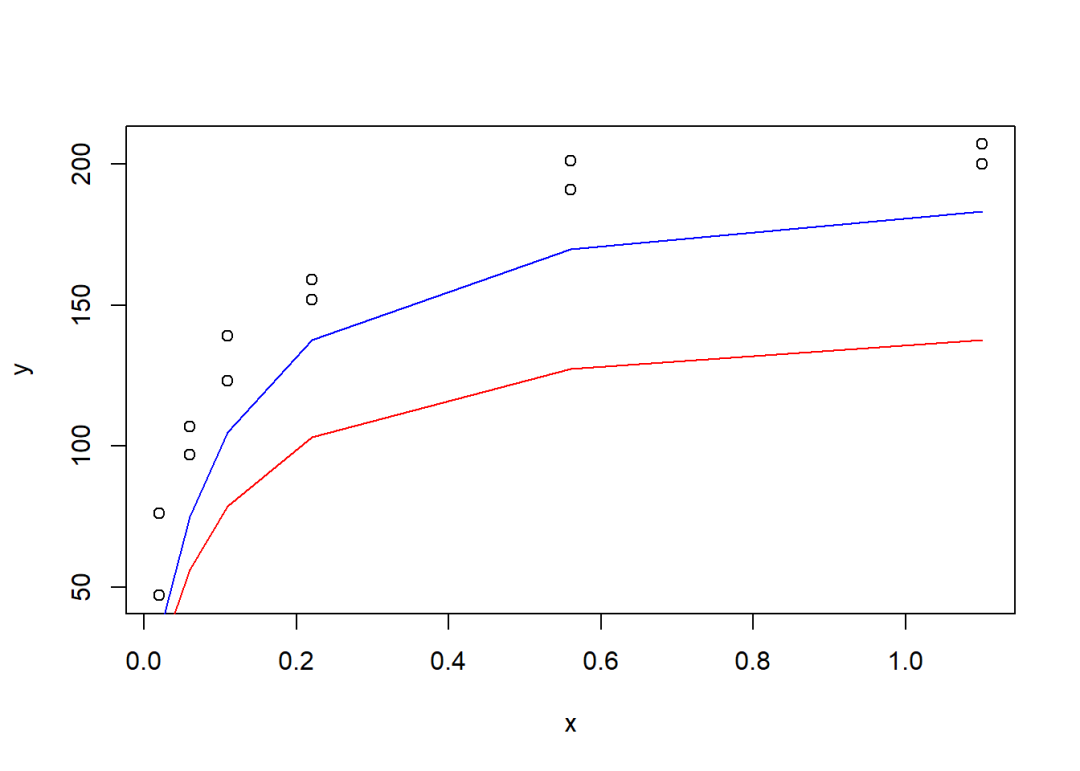
根据以上试验结果,可将200和0.1分别作为两个待定系数的初始值。
ls <- nlm(f, p = c(200, 0.1), x = data$x, y = data$y)
ls
## $minimum
## [1] 1195.449
##
## $estimate
## [1] 212.68384222 0.06412146
##
## $gradient
## [1] -0.000153498 0.093420975
##
## $code
## [1] 3
##
## $iterations
## [1] 26Note(s):
输出结果中
estimate元素的值就是系数的估计值。
plot(y ~ x, data = data)
x0 = seq(0, 1.1, 0.01)
y0 = ls$estimate[1]*x0/(ls$estimate[2] + x0)
lines(x0, y0, type = "l")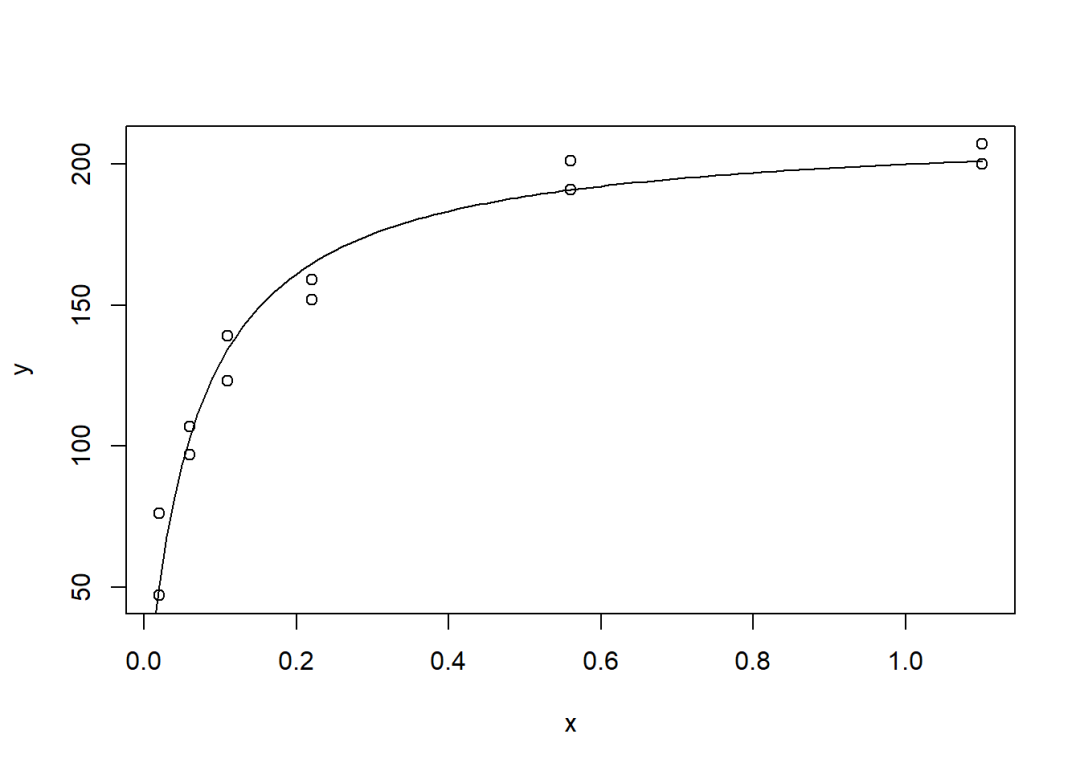
读者可自主尝试试验其他初始值的运行结果。
3 最大似然法
最大似然法(Maximum Likelihood)需要事先假设数据的分布模型,这里使用表示样本的概率分布函数。
因为每个样本取值相互独立,因此可用连乘法计算当前数据序列出现的概率为。最大似然估计的原则就是取能使该概率达到最大时的系数。因此,最大似然法的优化目标为:
随机事件的概率恒为正,因此可对其取对数,则优化目标可等价为如下形式:
对于本例,假设数据服从正态分布,即
在R语言中,可以使用dnorm()函数计算正态分布的概率密度值;当它的参数log = TRUE时,输出值为概率密度的自然对数。
nlm()函数的优化方向是求最小值,因此在定义目标函数时需要取其相反数,如下:
f2 <- function(p, x, y) {
sum(-dnorm(x = y, mean = (p[1]*x)/(x + p[2]), sd = 100,
log = T))
}
ml <- nlm(f2, p = c(200, 0.1), x = data$x, y = data$y)
ml
## $minimum
## [1] 66.34908
##
## $estimate
## [1] 212.68264765 0.06411974
##
## $gradient
## [1] 2.004515e-10 -3.979039e-07
##
## $code
## [1] 1
##
## $iterations
## [1] 25比较两种方法的估计结果:
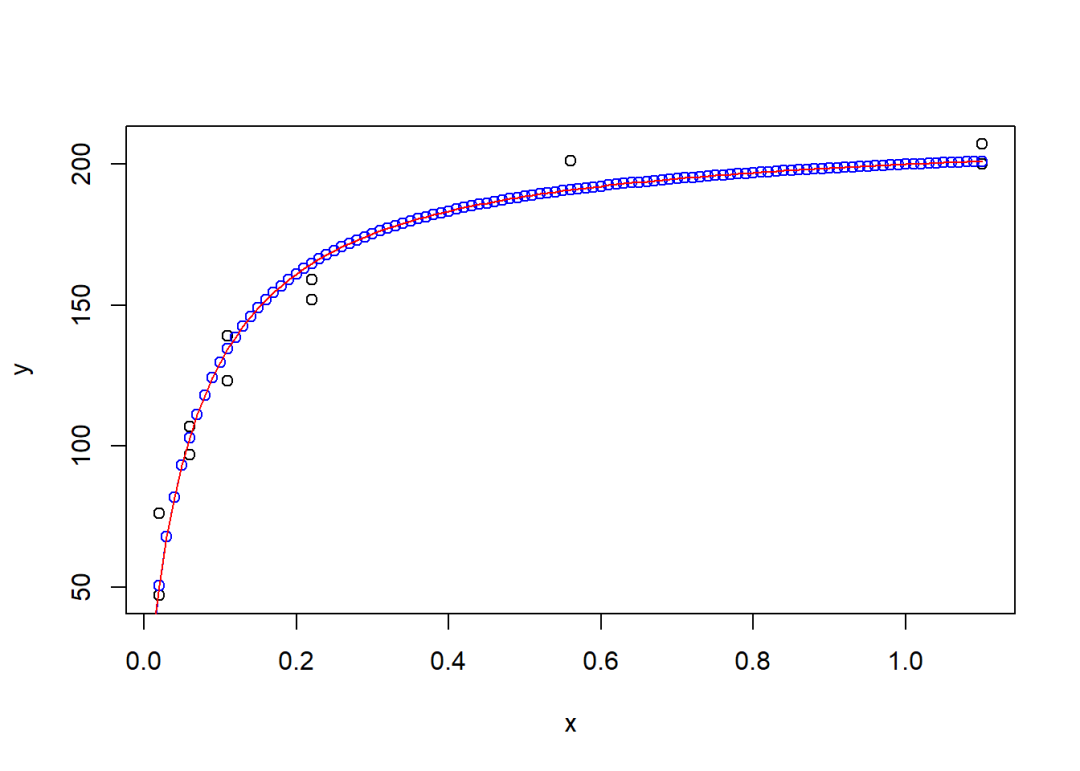
plot(y ~ x, data = data)
y0 = ls$estimate[1]*x0/(ls$estimate[2] + x0)
lines(x0, y0, type = "b", col = "blue")
y0 = ml$estimate[1]*x0/(ml$estimate[2] + x0)
lines(x0, y0, type = "l", col = "red")