数据库 | 事务相关知识点总结

news2024/9/29 9:34:13

本专栏收录了数据库的知识点，而从本文起，将讲述有关于数据库设计有关知识点，提供给有需要的小伙伴进行学习，本专栏地址可以戳下面链接查看

🎈 数据库知识点总结（持续更新中）：【数据库知识点】

🔑 数据库相关练习题（持续更新中）：【数据库练习题】

🔥 一个提供给Java学习者的专栏：【拼图小游戏（Java）】
🔎JavaWeb相关知识：【JavaWeb】

在这里插入图片描述

文章目录

一、概述
- 1.概念
- 2.实例
- 二、语法
- 1.开启事务
- 2.提交事物
- 3.回滚事物
三、特征
四、实例
- 1.开启事物
- 2.不开启事物
五、结语

一、概述

1.概念

数据库的事务（Transaction）是一种机制、一个操作序列，包含了一组数据库操作命令。

事务把所有的命令作为一个整体一起向系统提交或撤销操作请求，即这一组数据库命令要么同时成功，要么同时失败。

事务是一个不可分割的工作逻辑单元。

2.实例

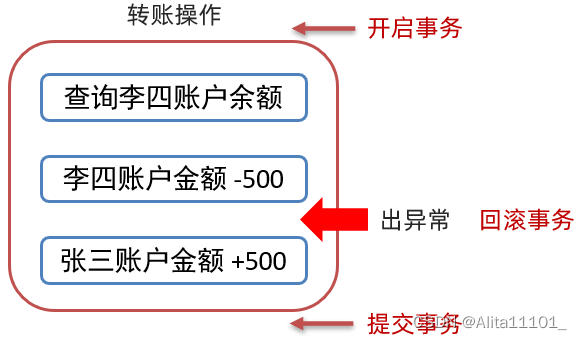
比如现李四需要转换500块钱给张三，具体的转账操作为

第一步：查询李四账户余额
第二步：从李四账户金额 -500
第三步：给张三账户金额 +500

现在假设在转账过程中第二步完成后出现了异常，第三步没有执行，就会造成李四账户金额少了500，而张三金额并没有多500；

这样的系统是有问题的。如果解决呢？

使用事务可以解决上述问题

在这里插入图片描述

二、语法

1.开启事务

START TRANSACTION;

BEGIN;

2.提交事物

提交事物可以理解为数据库在执行某个操作以后，要将操作的结果再返回给数据库，实现改变数据的效果（个人理解）所以提交事务的语句一般会写在SQL语句后面，回滚事物的上一条

COMMIT;

3.回滚事物

回滚事物可以理解为在出现异常的时候，将数据库内的数据恢复成开启事物之前的样子。比如上面的实例，如果出现异常的话，那么回滚事物也就意味着将张三和李四账户内的余额恢复成初始值，即我们第一次设定的值。

在JavaWeb中学到JDBC部分会写相关语句，就需要把回滚事物的语句写在catch中（try…catch语句）来抓取并处理异常

ROLLBACK;

三、特征

原子性（Atomicity）: 事务是不可分割的最小操作单位，要么同时成功，要么同时失败
一致性（Consistency） :事务完成时，必须使所有的数据都保持一致状态
隔离性（Isolation） :多个事务之间，操作的可见性
持久性（Durability） :事务一旦提交或回滚，它对数据库中的数据的改变就是永久的

四、实例

1.开启事物

首先我们定义一张user的表，这里查询一下
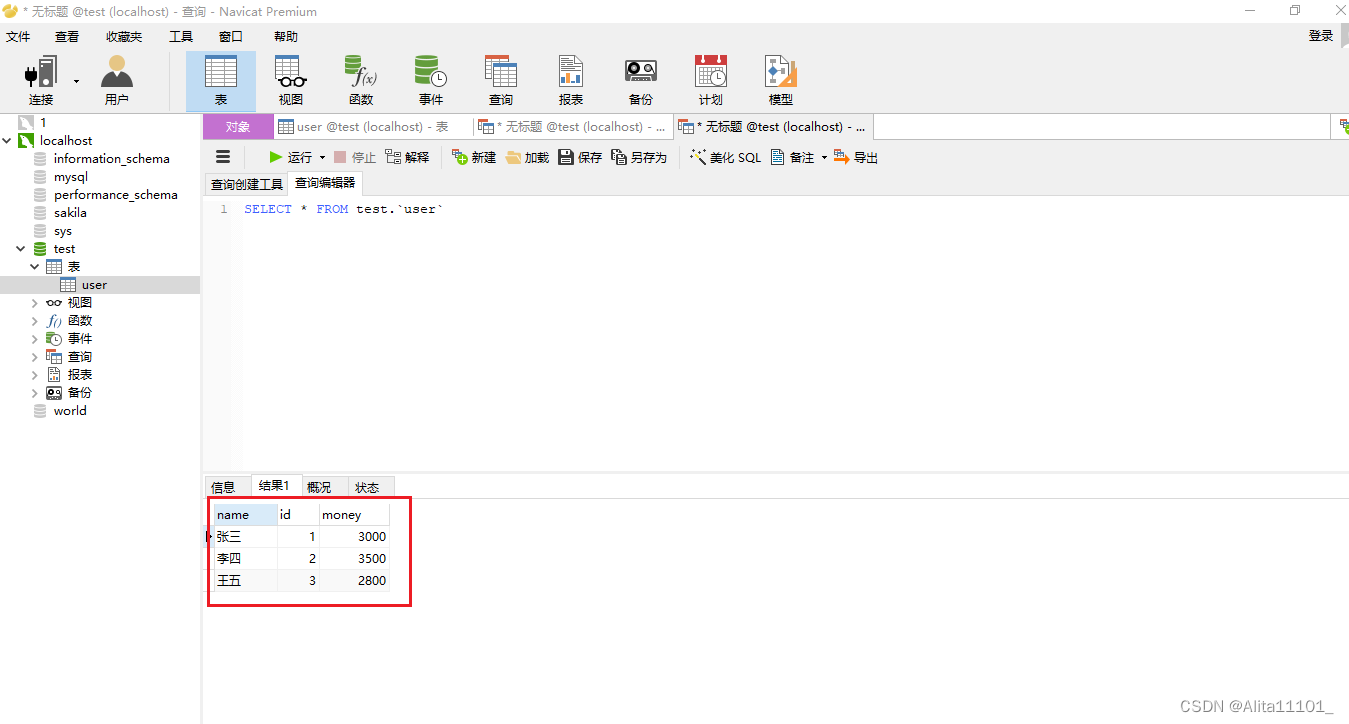
在这里插入图片描述
然后我们执行一个有错误的SQL语句

  -- 开启事务
  BEGIN;
  -- 转账操作
  
  -- 2. 李四账户 -500
  UPDATE `user` set money = money - 500 where name = '李四';
  
  -- 此处不是注释，在整体执行时会出问题，后面的sql则不执行
  出现异常了...
    
  -- 3. 张三账户 +500
  UPDATE `user` set money = money + 500 where name = '张三';
  
  -- 提交事务
  COMMIT;
  
  -- 回滚事务
  ROLLBACK

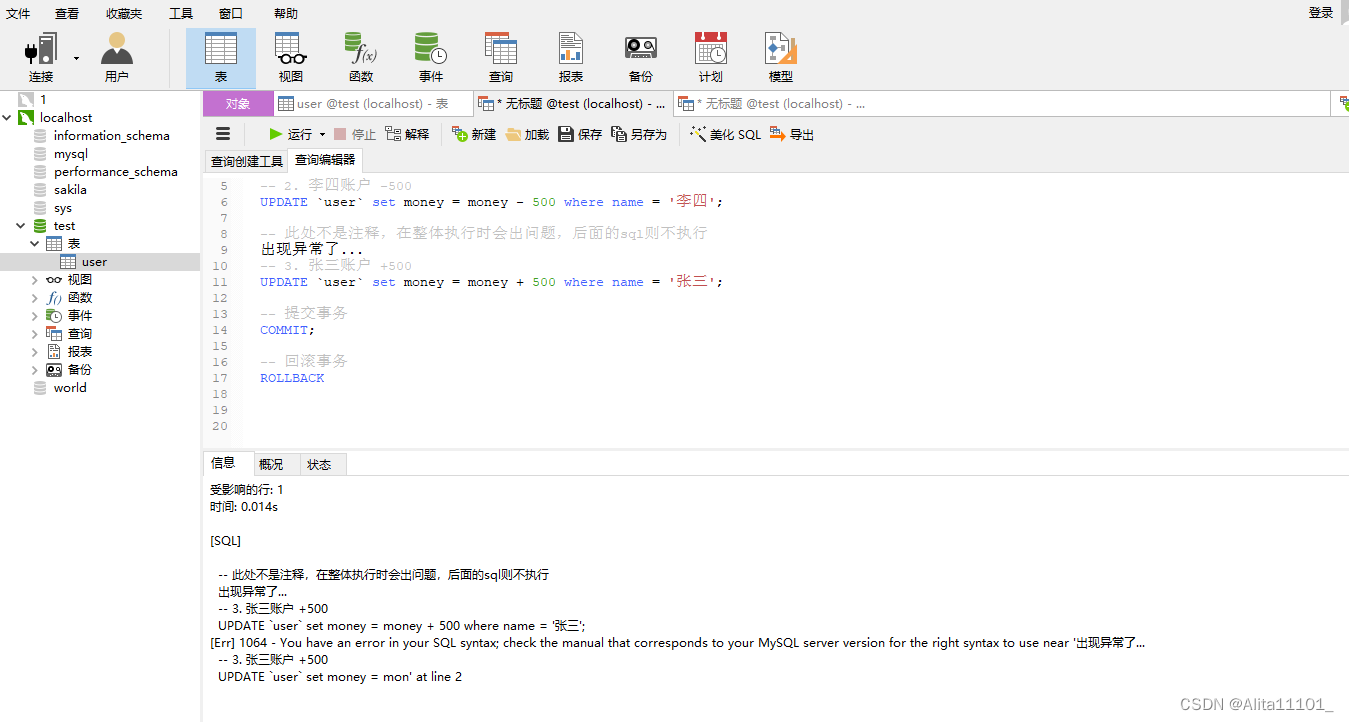
在这里插入图片描述

再来查询一下，发现数据没有变化
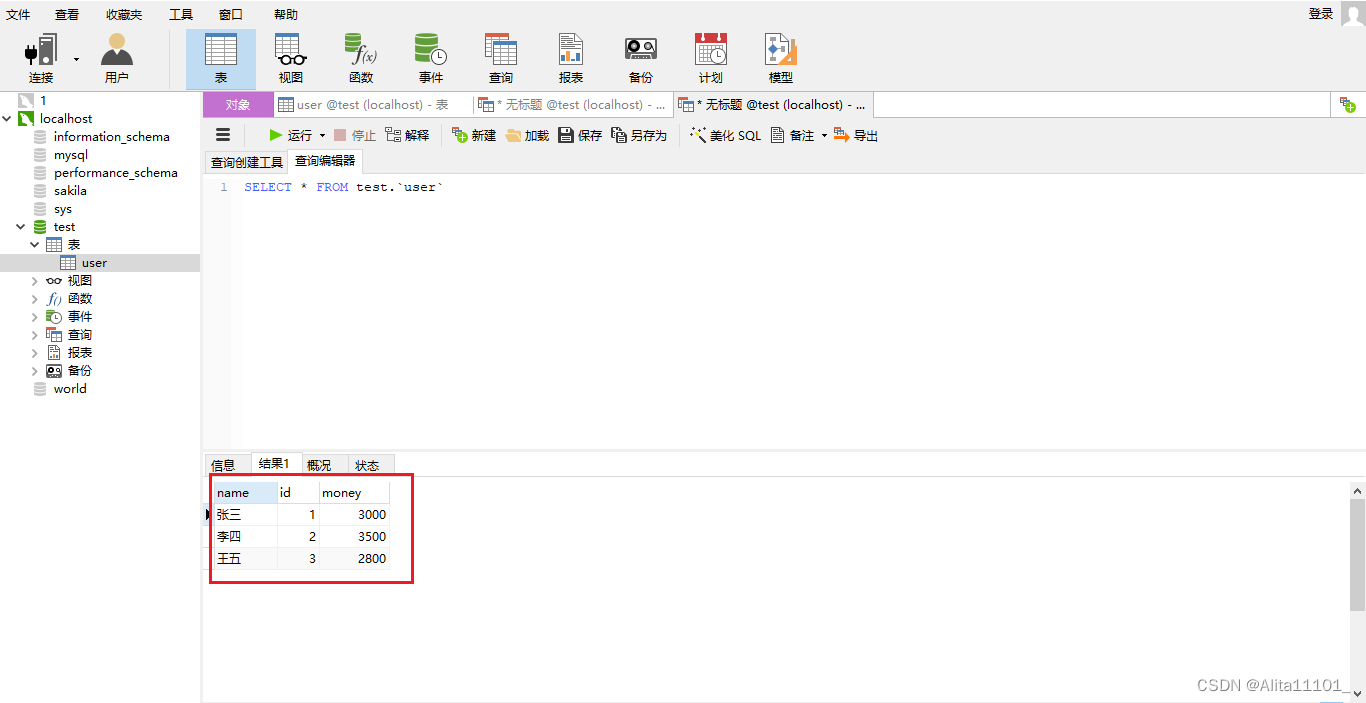
在这里插入图片描述

2.不开启事物

-- 李四账户 -500
UPDATE `user` set money = money - 500 where name = '李四';
  
-- 此处不是注释，在整体执行时会出问题，后面的sql则不执行
  出现异常了...  
  
--张三账户 +500
UPDATE `user` set money = money + 500 where name = '张三';