GCD

最大公约数Greatest Common Divisor(GCD)：整数a和b的GCD是指能同时整除a和b的最大整数，记为gcd(a,b)。由于-a的因子和a的因子相同，因此gcd(a, b)= gcd(al, |bl)。编码时只关注正整数的最大公约数。

GCD性质

(1) gcd(a, b)= gcd(a, a+b)= gcd(a, k·a+b)

(2） gcd(ka,kb)=kgcd(a,b)
(3）定义多个整数的最大公约数:gcd(a, b, c)= gcd(gcd(a, b),c)。
(4）若gcd(a, b)= d，则gcd(a/d, b/d)= 1，即a/d与b/d互素。这个定理很重要。
(5) gcd(a+cb, b)= gcd(a, b)

Python库函数gcd()和手写代码

Python函数gcd()

gcd()不会返回负数 ( c++函数std::_gcd()可以返回负数)
gcd()可以带多个参数

from math import *
print(gcd(15,81))        # 3

# 0与其他数b的最大公约数没有意义，但会输出b
print(gcd(0,44))         # 44
print(gcd(0,0))          # 0

print(gcd(-6,-15))       # 3  所有数的最大公约数都是正数
print(gcd(-17,289))      # 17
print(gcd(17,-289) )     # 17
print(gcd(48,96,120,688))# 8 多个数的公约数

手写GCD代码

手写gcd函数，常用欧几里得算法。
辗转相除法求gcd：gcd(a,b) = gcd (b,a mod b) mod：取余
这是最常用的方法，极为高效。
设a > b，辗转相除法的计算复杂度为O( $log_2a^3$ )。

可能输出负数，和库函数不同。若不需要输出负数可以将第二行代码的a改成abs(a)。

注意：一次只能求两个数的最小公倍数，求n个数的需要求n-1次。

def gcd(a, b):
    if b==0: return a # 不需要输出负数可以将a改成abs(a)
    else:    return gcd(b, a%b)
print(gcd(15,81))  # 3

# 第二个数为负数才输出负数
print(gcd(-6,-15)) # -3
print(gcd (-17,289))# 17
print(gcd(17,-289)) # 17

LCM

最小公倍数LCM ( the Least Common Multiple）。
a和b的最小公倍数lcm(a, b)，从算术基本定理推理得到。
算术基本定理:任何大于1的正整数n都可以唯一分解为有限个素数的乘积: $n=p_1^{c1}p_2^{c2}...p_m^{cm}$ ，其中 $c_i$ 都是正整数， $p_i$ 都是素数且从小到大。

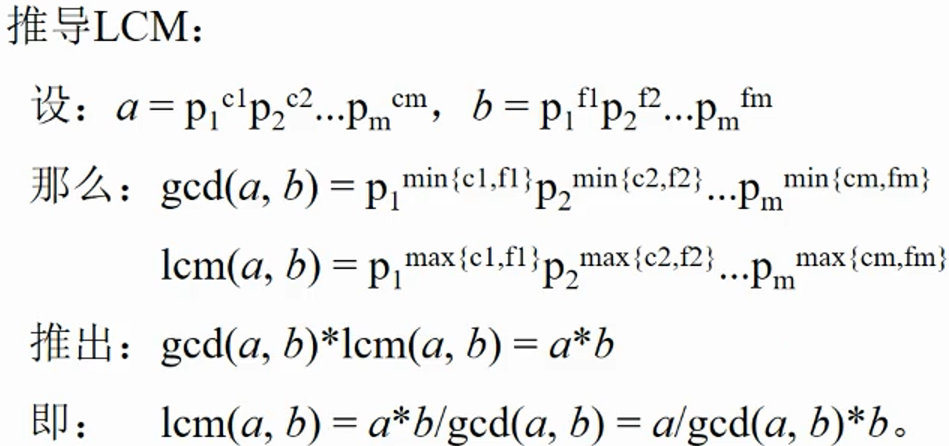
结论：lcm(a,b) = a*b/gcd(a,b) = a/gcd(a,b)*b （c++先除后乘，避免溢出）

Python库函数lcm()和手写代码

1、库函数lcm()

在Python新版本(Python3.9才加入了lcm）中有库函数lcm()，它可以带多个参数。

from math import *
print(lcm(3,6,8,9))  # 72

2、手写lcm()

在Python的旧版本中并没有lcm()函数，自己写一个lcm():

from math import *
def lcm(x, y):
    return x*y//gcd(x, y)

例题一：核桃的数量

2013年第四届省赛lanaiaoOJ题号210

题目描述

小张是软件项目经理，他带领 3 个开发组。工期紧，今天都在加班呢。为鼓舞士气，小张打算给每个组发一袋核桃（据传言能补脑）。他的要求是：

各组的核桃数量必须相同

各组内必须能平分核桃（当然是不能打碎的）

尽量提供满足 1,2 条件的最小数量（节约闹革命嘛）

输入描述

输入一行 a,b,c，都是正整数，表示每个组正在加班的人数，用空格分开(a,b,c<30)。

输出描述

输出一个正整数，表示每袋核桃的数量。

输入输出样例

输入
2 4 5
输出
20

简单题，答案就是三个数字的最小公倍数。

from math import*
def lcm(x, y):
    return x//gcd(x, y)*y
a,b,c = map(int,input ().split())
k = lcm(a, b)
print(lcm(k,c))

例题二：等差数列

2019年第十届省赛，lanqiao0J题号192

题目描述

数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列，只记得其中 N 个整数。

现在给出这 N 个整数，小明想知道包含这 N 个整数的最短的等差数列有几项？

输入描述

输入的第一行包含一个整数 N。

第二行包含 N 个整数 1,2,⋅⋅⋅,A1,A2,⋅⋅⋅,AN。(注意 A1 ∼ AN 并不一定是按等差数列中的顺序给出)

其中，2≤N≤ $10^5$ ，0≤ $A_i$ ≤ $10^9$ 。

输出描述

输出一个整数表示答案。

输入输出样例

输入
5
2 6 4 10 20
输出
10
样例说明：包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、 18、20。

思路

所有数字间距离最小的间隔是公差吗?
并不是，例如{2，5，7}，最小的间隔是2，但公差不是2，是1。
间隔的最小公因数是公差：这是gcd问题。把n个数据排序，计算它们的间隔，对所有间隔做GCD，结果为公差。
最少数量等于：(最大值-最小值) / 公差+1。

from math import *
n = int (input())
a = list(map(int,input().split() ))
a. sort () # 原地排序
d = 0
for i in range (1, n):
    d = gcd (d, a[i]-a[i-1])
if d == 0:            # 公差为0
    print (n)
else:
    print((a[-1]-a[0])//d + 1)

例题三、 Hankson的趣味题

Hankson的趣味题 lanqiao0J题号520

题目描述

在课堂上，老师讲解了如何求两个正整数 c1 和 c2 的最大公约数和最小公倍数。现在 Hankson 认为自己已经熟练地掌握了这些知识，他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”，这个问题是这样的：已知正整数 a0,a1,b0,b1，设某未知正整数 x 满足：

x 和 a0 的最大公约数是 a1；

x 和 b0 的最小公倍数是 b1。

Hankson 的“逆问题”就是求出满足条件的正整数 x。但稍加思索之后，他发现这样的 x 并不唯一，甚至可能不存在。因此他转而开始考虑如何求解满足条件的 x 的个数。请你帮助他编程求解这个问题。

输入描述

第一行为一个正整数 n，表示有 n 组输入数据。

接下来的 n 行每行一组输入数据，为四个正整数 a0，a1，b0，b1，每两个整数之间用一个空格隔开。输入数据保证 a0 能被 a1 整除，b1 能被 b0 整除。

其中，保证有 1≤a0，a1，b0，b1≤2× $10^9$ 且n≤2000。

输出描述

输出共 n 行。每组输入数据的输出结果占一行，为一个整数。

对于每组数据：若不存在这样的 x，请输出 0；若存在这样的 x，请输出满足条件的 x 的个数；

输入输出样例

输入
2
41 1 96 288
95 1 37 1776 
输出
6
2

问题解析

1、暴力法

from math import *
def lcm(x, y):
    return x//gcd(x, y)*y

n = int(input())
for i in range(n):
    ans = 0
    a0,a1,b0,b1 = map(int,input().split())
    for x in range(1,b1+1):                  # x的最大可能值为b1
        if gcd (x, a0)==a1 and lcm(x, b0)==b1:
            ans +=1
    print(ans)

本题n≤2000，x的范围:x≤b1，而b1≤2× $10^9$ ，O(n*b1)=4* $10^{12}$ ，超过蓝桥杯规定的 $10^8$ ，故超时了。

2、优化

若x是b1的因子，有x*y = b1，y也可能是答案。
只需要在范围x<=sqrt(b)内查询，同时判断y就行了。
但还是超时，因为gcd计算也要花时间，加上一个优化: if b1%x==0，表示b1是x的公倍数。

from math import*
def lcm(x, y):
    return x//gcd (x, y)*y
n = int(input ())
for _ in range (n):
    a0, a1, b0, b1 = map(int, input().split())
    ans = 0
    for x in range(1,int(sqrt(b1))+1):
        if b1 % x ==0:      #若b1是x的公倍数
            if gcd(x, a0) ==a1 and lcm(x, b0)==b1: ans+=1
            y = b1//x
            if x==y : continue    # 重复了，跳过
            if gcd(y, a0)==a1 and lcm(y, b0)==b1: ans+=1
    print(ans)

例题四：最大比例

2016年第七届省赛lanqiao0J题号120

题目描述

X 星球的某个大奖赛设了 M 级奖励。每个级别的奖金是一个正整数。并且，相邻的两个级别间的比例是个固定值。也就是说：所有级别的奖金数构成了一个等比数列。比如：16,24,36,54，其等比值为：3/2

现在，我们随机调查了一些获奖者的奖金数。请你据此推算可能的最大的等比值。

输入描述

第一行为数字 N (0<N<100)，表示接下的一行包含 N 个正整数

第二行 N 个正整数 Xi(Xi<109)，用空格分开。每个整数表示调查到的某人的奖金数额

输出描述

一个形如 A/B 的分数，要求 A、B 互质。表示可能的最大比例系数测试数据保证了输入格式正确，并且最大比例是存在的。

输入输出样例

输入
3
1250 200 32
输出
25/4

思路：

把这些数字排个序，然后算出相邻两个数的比值。
最小的那个比值K是否就是答案呢?
不是。例如{2,16, 64}，比值是16/2=8，64/16=4，最小比值K=4。但原序列是{2,4,8,16,32,64}，比值是2。
答案可能比K小，如何求出答案?如果一个个试比K小的分数，肯定会超时。

换一个思路：

不是算相邻两个数的比值，而是每个数对第一个数的比值。
设原序列是 $\{x,xq^{1},xq^2...,q^{n-1}\}$ ,q为公比，从中挑出一些数字 $\{xq^c,xq^{d}...,xq^{y},xq^z\}$ ,它们之间的两两相除，得到一个比值序列 $\{1,q^{d-c},...,q^{z-y}\}$ ，这其中的一些数字可能是相同的。算它们对第一个数的比值，得 $\{1,q^{d-c},...,q^{y-c},q^{z-c}\}$ $=\{1,q^{kd},...,q^{ky},q^{qkz}\}$ ，这个序列内的所有数字肯定不同。
令q= a/b，这个序列变成了 $\{1, (a/b)^{kd}, .... (a/b)^{ky}, (a/b)^{kz}\}$
分成分子和分母两个序列，分别是 $A=\{a^{kd},...,a^{ky}, a^{kz}\}, B=\{ b^{kd}, .... b^{ky}, b^{kz}\}$ 。
已知这两个序列A、B中每个元素的值，求a和b。

举例：A={16,128,512,1024}，得a=2，即 $A=\{2^{4},2^{7},2^{9},2^{10}\}$

如何根据A求a?
显然，A中每个数除以前面一个数，都能够整除，得到a的一个倍数，但是这个倍数还不是a，需要继续除，直到系列中出现1为止，就得到a。以前2个数 $\{2^{4},2^{7}\}$ 为例，计算步骤是: $2^{7}/2^{4}=2^{3},2^{4}/2^{3}=2^{1}$ , $2^{3}/2^{1}=2^{2},2^{2}/2^{1}=2,2^{1}/2^{1}=1$ ，结束，得a=2。这是一个辗转相除的过程。
对A中所有元素都执行这个过程，就得到了a。

代码

from math import *
# 得到除1外的最小公因数
def gcd_sub(a, b):
    if a<b: a,b = b, a # 交换，保证a>b
    if b==1: return a
    return gcd_sub(b, a//b)
n = int(input())
x = list(set(map(int,input ().split()))) # set有去重的作用,万一输入有相同的数
x.sort ()
n = len(x)
a = []
b =[]
for i in range(1, n):
    d = gcd(x[i],x[0])  # 与第一个数求比值
    a.append(x[i]//d)   # A序列
    b.append(x[0]//d)   # B序列
n = len(a)
up = a[0]   # 分子
down = b[0] # 分母
# 求分子分母的最小公因数
for i in range(1,n):
    up = gcd_sub(up, a[i])
    down = gcd_sub(down,b[i])
print('%d/%d'%(up, down))

例题五：寻找整数

2022年第十三届省赛，填空题，lanaiao0J题号2131

问题描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

有一个不超过 $10^{17}$ 的正整数 n，知道这个数除以 2 至 49 后的余数如下表所示，求这个正整数最小是多少。

解法一：模拟

暴力法:一个个检验1～ $10^{17}$ 的每个数
由于这个数n最大可能是 $10^{17}$ ，验证的时间太长。

如何减少验证时间?

如果n是某个数k的倍数，那么可以递增k来验证，for i in range(1, $10^{17}$ ,k)，循环 $10^{17}$ /k次，k越大，验证的次数越少。
从表中看出n是11和17.的倍数,最小的k =11×17=187。
但是k仍然太小, $10^{17}$ /187≈ $10^{14}$ ，for循环 $10^{14}$ 次仍然耗时太长。（即使用C++编码运行，也需要 $10^6$ 秒)

如何找到一个较大的k?

证明：满足表格中部分（例如a= 45，46，47，48，49)的n，从小到大的n1、n2、n3、...，它们是一个等差数列，即n2-n1,= n3-n2= ...=k'。

cnt = 0
tmp=0
for i in range(187,10**17,187):
    if i % 49 ==46 and i % 48== 41 and i % 47 == 5 \
                   and i % 46 == 15 and i % 45 == 29:
        cnt += 1
        print(i,'k=', i-tmp)    # i-tmp是两次满足这五个要求的公差
        tmp=i
    if cnt > 3: break
# 5458460249 k= 5458460249
# 12590206409 k= 7131746160
# 19721952569 k= 7131746160
# 26853698729 k= 7131746160

先用Python编码求k'：得k'=7131746160，故从5458460249开始，步长k=7131746160的等差数列

完全满足表格的从小到大的n1、n2、n3、...，也是等差数列
n2-n1 = n3-n2= ... =k。k是k’的倍数。（因为满足后五个要求是满足全部要求的子条件）
用k’=7131746160作为for循环的步长暴力检验找到最小的n。
循环次数:1017/k’~14,000,000。

代码演示1

mod = [0,0,1,2,1,4,5,4,1,2,9,0,5,10,11,14,9,0,11,18,9,11,11,15 ,17,9,23,20,25,16,29,27,25,11,17,4,29,22,37,23,9,1,11,11,33,29,15,5,41,46]
for i in range (5458460249,10**17,7131746160):     #开始是5458460249,步长k=7131746160
    for a in range(2,50):
        if i % a != mod[a]:
            break
    else:               # for else结构: 若for正常结束,运行else语句
        print(i)        # 输出答案:2022040920220409
        break

解法二：LCM

从表格的第一个数2开始，逐个增加后面的数，找满足条件的n。
1）满足第一个条件，除以2余1的数有:3、5、7、9、...此时步长k= 2。

2）继续满足第二个条件，除以3余2的数，只能从上一步骤的3、5、7、9、...中找，有5、11、17、...
此时步长k =6，为什么k=6?

实际上是LCM: k = lcm(2,3)=6

证明:
设n1和n2满足:
n1= 2a1+1= 3b1+2
n2= 2a2+1 = 3b2+2
n2和n1的差k = n2-n1= 2(a2-a1)= 3(b2-b1)
k是2的倍数，也是3的倍数，那么k是2和3的最小公倍数，k= lcm(2,3)=6。

3）继续满足第三个条件，除以4余1的数，只能从5、11、17、...中找，有5、17、29、...此时步长k = lcm(2,3,4)= 12。

4）继续满足第四个条件，....

逐个检查表格，直到满足表格中所有的条件。

代码演示2

代码计算量极小，只需要对表格中的2~49做48次LCM即可。

from math import *

mod = [0, 0, 1, 2, 1, 4, 5, 4, 1, 2, 9, 0, 5, 10, 11, 14, 9, 0, 11, 18, 9, 11, 11, 15, 17, 9, 23, 20, 25, 16, 29, 27,
       25, 11, 17, 4, 29, 22, 37, 23, 9, 1, 11, 11, 33, 29, 15, 5, 41, 46]
ans = 2 + mod[2]
k = 2  # 从第一个数的步长2开始
for i in range(3, 50):
    while 1:
        if ans % i == mod[i]:   # ans是满足前i个数的解
            k = lcm(k, int(i))  # 对当前步长k和i做LCM得到新的步长
            break
        else:
            ans += k            # ans不满足就累加当前步长k,直到ans满足前i个数的解
print(ans)