【C++算法图解专栏】一篇文章带你掌握高精度加减乘除运算

✍个人博客：https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
📣专栏定位：为 0 基础刚入门数据结构与算法的小伙伴提供详细的讲解，也欢迎大佬们一起交流~
📚专栏地址：https://blog.csdn.net/Newin2020/article/details/126445229
❤️如果有收获的话，欢迎点赞👍收藏📁，您的支持就是我创作的最大动力💪
🎏唠叨唠叨：在这个专栏里我将会整理 PAT 甲级的真题题解，并将他们进行分类，方便大家参考。

高精度

C++ 本身自带的数字类型无法解决特别大的数的运算，会出现溢出的情况，这时候我们就需要一些算法来模拟大数的运算过程，从而得到最终的结果。

接下来我将带领大家学会高精度的加减乘除运算，这样以后再遇到类似问题就不用再怕啦！

高精度加法

前提条件：给定两个正整数（不含前导0）

不知道大家是否记得小学学的加法运算，把需要运算的两个数列出来，运算过程中可能会出现进位的情况，举个例子，我们来计算一下 48673 和 93146 的和：

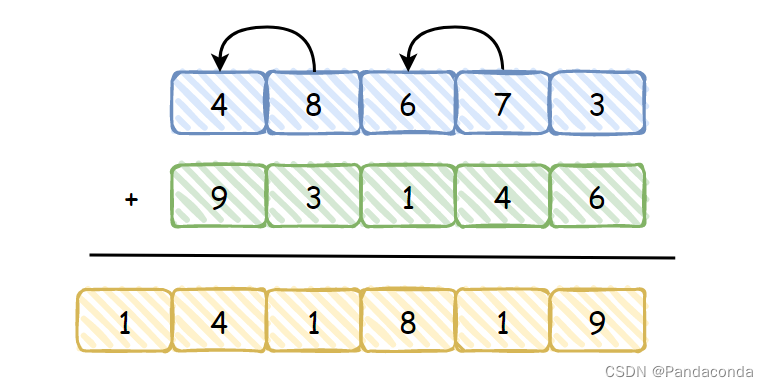
动手计算其实很简单，但是如果要用程序实现出来就有点难了，直接上步骤：

首先我们在输入时就不能用整型类型输入，而是用字符串类型。
然后将字符串中的字符转换成数字传入数组当中（ vector 作为数组），这样我们就得到了两个数组 A 和 B，注意我们传入数组时，不能按照字符串下标从低到高的顺序传入，而是反过来，将数字的最低位放到数组中下标的最低位，还是拿上面的那个例子举例。
然后开始模拟两个数的加法运算，这里我们需要用到一个附加位 t 来记录每一位上的和，从而解决进位的问题，并且用一个新的数组 C 来接收计算结果，还是上面的例子。

可以发现，第一位上的和没有大于 10，所以直接将 t 加入数组 C 中，接下来继续看大于 10 的情况。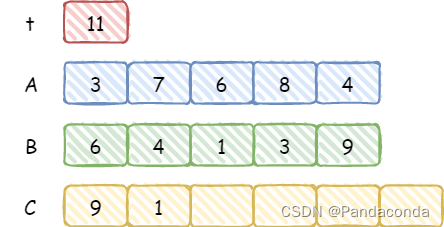

这时候我们将 t%10 的结果放入 C 中，然后执行 t/10 并保留至下一次计算，可以发现这样就模拟了进位操作，我们再看下一位，由于 t/10=1 ，故这次计算需要加上这个 1 即 6+1+1=8 ，并放入 C 当中。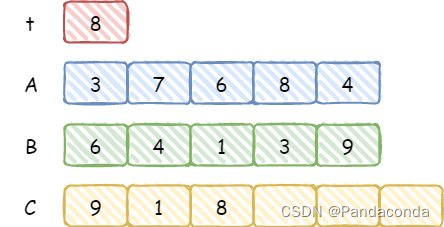

第四位运算同理。

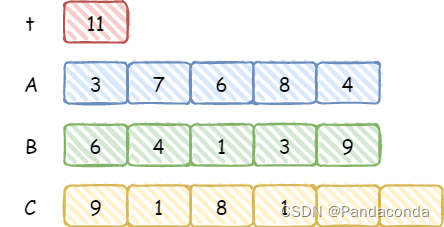
最后一位需要额外注意一下，如果运算已经结束，如果 t 不为 0，则需要加到数组后面。
最后，我们再将数组 C 倒着输出一遍就得到了最终的运算结果。

#include <bits/stdc++.h>
using namespace std;

//高精度加法
vector<int> Add(vector<int>& A, vector<int>& B) {
	vector <int> C;
	int t = 0;
	for (int i = 0; i < A.size() || i < B.size(); i++)
	{
		if (i < A.size()) t += A[i];
		if (i < B.size()) t += B[i];
		C.push_back(t % 10);
		t /= 10;
	}
	if (t)   C.push_back(t);	//加上最高位的进位
	return C;
}

int main() {
	string a, b;
	vector<int> A;
	vector<int> B;
	cin >> a >> b;
    //将字符转换成数字
	for (int i = a.size() - 1; i >= 0; i--) {
		A.push_back(a[i] - '0');
	}
	for (int i = b.size() - 1; i >= 0; i--) {
		B.push_back(b[i] - '0');
	}
	vector<int> C = Add(A, B);
	for (int i = C.size() - 1; i >= 0; i--) {
		cout << C[i];
	}
}

高精度减法

前提条件：给定两个正整数（不含前导0）

其实高精度减法和加法有一定相似度，但是会多几个步骤，我们还是用上面的两个数字手动先计算一下 93146 和 38673 的差：

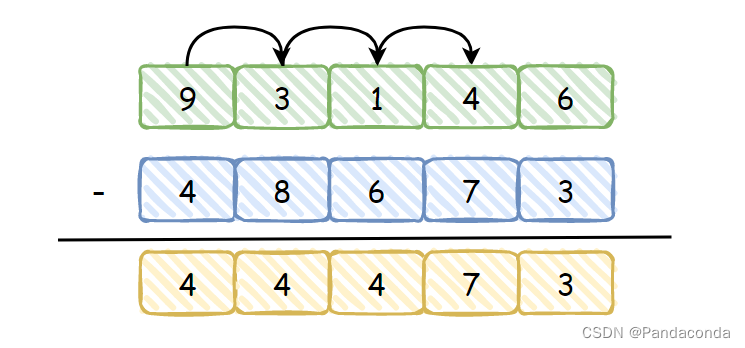
可以发现，对于减法运算我们需要考虑的不再是往前进位的问题，而是往前借位的问题，直接上步骤：

同样，将输入的字符串转换为数字放入数组，数字的低位要对应数组下标的低位。
然后这里就和加法不同了，减法需要注意到结果的正负问题，而加法无需考虑，所以需要判断这两个数谁大谁小。因为给定的是两个正整数，故只需判断两个数的长度，如果长度相等在分别进行判断。根据上述结果来判断是否要在前面加上负号，如果前面的数更小，则结果需要加上负号。
我们仍然需要用到一个附加位 t ，只不过这里是用来记录每一位上的差值，还是用上面的例子进行模拟。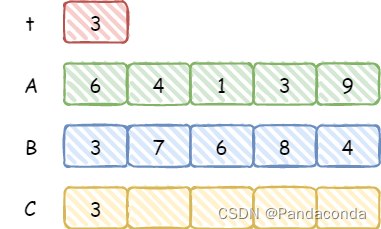

第一位由于没有出现负数的情况，所以直接将 t 放入数组 C 即可，注意这里用完 t 后需要将其置 0 以免干扰后续的运算，接下来看出现负数的情况。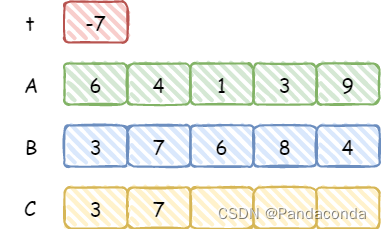

可以发现，4-7=-7 出现了负数的情况，这时候就不能直接放入 C 中，而是往前借一位然后再放入 C 中，即将 (-7+10)%10=7 放入 C 中。注意这里并不是在 t 上修改，因为 t 后面还要进行判断，如果 t 为负数的话需要将 t 置为 1，否则就像上面一样置为 0（这部分可以配合后面 Sub 函数的那块代码一起理解）。我们再继续看第三位的运算。

由于第二位的运算出现了负数，导致 t 被置为 1，所以我们需要额外减去这个 1，因为这是低位向高位借的一位，所以可以看到第三位结果为 ((1-1-6)+10)%10=(-4+10)%10=4，同样第三位也向高位借了一位，也需要将 t 置为 1，然后继续运算。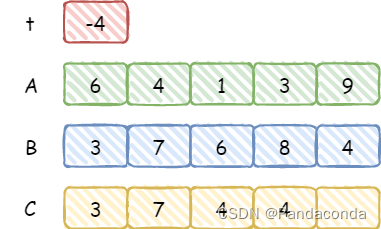

最后两位同理，我们可以得到最终的运算结果。注意，如果高位计算后为 0 即出现了前导 0 则需要去除。
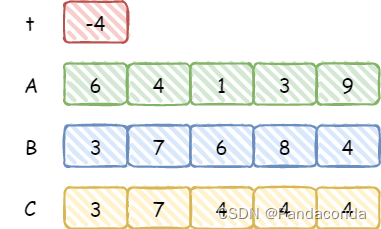
最后输出的时候，倒序输出 C 中数字就是最终的答案。

#include<bits/stdc++.h>
using namespace std;

//高精度减法
vector<int> Sub(vector<int>& a, vector<int>& b)
{
	vector<int> c;
	int t = 0;
	for (int i = 0; i < a.size(); i++)
	{
		t = a[i] - t;
		if (i < b.size())  t -= b[i];
		c.push_back((t + 10) % 10);
		if (t < 0) t = 1;
		else t = 0;
	}
	while (c.size() > 1 && c.back() == 0)  c.pop_back();	//去除前导0
	return c;
}

bool check(vector<int> a, vector<int> b)
{
	if (a.size() > b.size())   return true;
	else if (a.size() < b.size())  return false;
	for (int i = a.size() - 1; i >= 0; i--)
	{
		if (a[i] != b[i])   return a[i] > b[i];
	}
	return true;
}

int main() {
	string a, b;
	vector<int> A;
	vector<int> B;
	cin >> a >> b;
    //将字符转换成数字
	for (int i = a.size() - 1; i >= 0; i--) {
		A.push_back(a[i] - '0');
	}
	for (int i = b.size() - 1; i >= 0; i--) {
		B.push_back(b[i] - '0');
	}
    //判断两者谁大
	if (check(A, B))
	{
		vector<int> C = Sub(A, B);
		for (int i = C.size() - 1; i >= 0; i--) {
			cout << C[i];
		}
	}
	else
	{
		vector<int> C = Sub(B, A);	//需要将更大的那个放到第一个参数
		cout << "-";
		for (int i = C.size() - 1; i >= 0; i--) {
			cout << C[i];
		}
	}
}

高精度乘法

前提条件：给定两个非负整数（不含前导0）

其实高精度乘法操作与高精度加法操作比较类似，我们先回顾一下手动的乘法操作，假设我们要计算 4139 × 324 的结果：

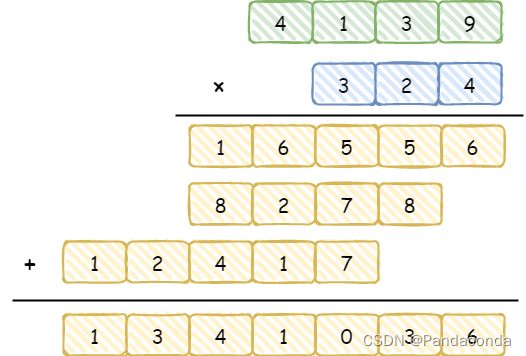
也就是说第二个数的每一位都要和第一个数相乘得到结果，每计算一次结果都要左移一位，最后再将这些结果相加，而我们实现的思路也是这样，直接上步骤：

一开始还是先将数据用字符串读入，只不过这里我们只将第一个数用字符串读入，而第二个数直接用整型类型接收即可，然后将读入的字符串转换成数字放到数组 A 中，注意这里还是低位数字放在数组的低位下标。
然后开始进行计算，我们这里用到的附加位 t 使用来保存每一位乘积累加的结果，这么说其实有点不准确，直接上例子，还是上面的 4149 × 324，来看看具体是如何操作的。注意，我们这里模拟的操作放到下面代码中，324 就是第一个传入参数，4149 就是第二个传入参数。

可以发现 t=4*4139=16556，由于在手动计算时，每次计算都会往左移一位，所以每次计算结果的最后一位一定是可以确定下来的，故直接将 16556%10=6 放入 C 中，然后进行 t/10 的操作，再继续看下一位。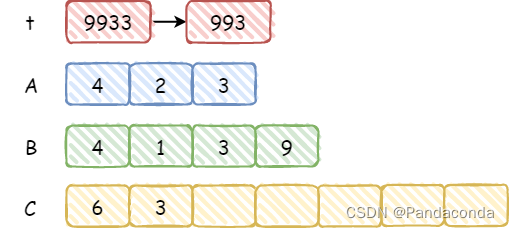

这里在进行完第二位和 B 的乘法操作后，还要加上上一位保留下来的 t 即 t=1655+2*4139=9933，这其实在进行乘法运算的过程中同步模拟了后面的加法运算，因为每次计算完后得到的结果的最后一位一定是确定的，再来看最后一位。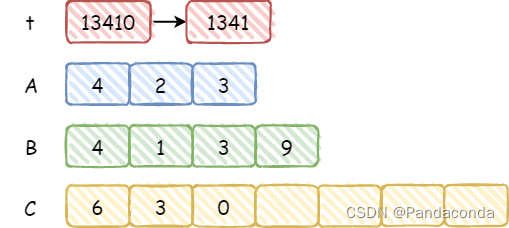

和上一步相同，t=993+3*4139=13410，然后将最后一位推入 C 中。最后由于 t 不为 0 但所有乘法操作已经进行完了，所以将 t 按照逆序将剩余的数字推入 C 中。另外，如果结尾有多余的 0，需要去除掉，例如乘数中有一个为 0，那么上述的操作得到的结果都为 0，但是输出时只能输出一个 0。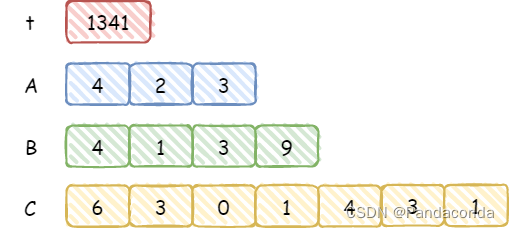
将 C 中的数字逆序输出就是最终的结果。

#include<bits/stdc++.h>
using namespace std;

//高精度乘法
vector<int> Mul(vector<int> a, int b)
{
    vector<int> c;
    int t = 0;
    for (int i = 0; i < a.size() || t; i++)
    {
        if (i < a.size())  t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    //处理其中一个乘数为0的情况
    while (c.size() > 1 && c.back() == 0)  c.pop_back();
    return c;
}

int main()
{
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    //将字符转换成数字
    for (int i = a.size() - 1; i >= 0; i--)
    {
        A.push_back(a[i] - '0');
    }
    vector<int> c = Mul(A, b);
    for (int i = c.size() - 1; i >= 0; i--)
    {
        cout << c[i];
    }
}

高精度除法

前提条件：给定两个非负整数（不含前导0）

高精度除法和前面就有些不一样了，它的运算比较特殊，我们先来看看手动运算，假设我们要计算 4108 / 12 的结果：

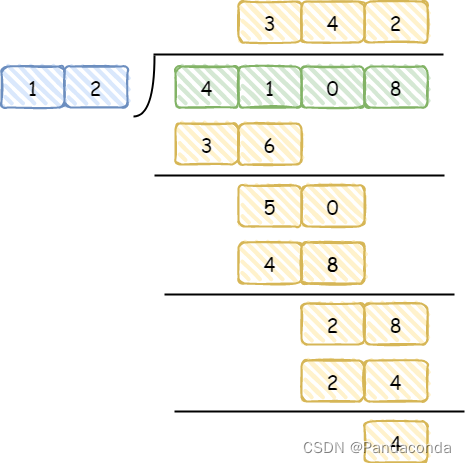
可以发现一个和前面运算不同的情况，除法运算时从高位开始计算，而加减乘都是从低位开始计算的，所以在代码实现的时候也有有所改变。

另外，我们上面计算其实省略掉了开头的 0，在 4108 第一次除以 12 的时候，会从 4108 的第一个数开始除，发现 4 除以 12 不够，所以会直接填上 0 并将 4 乘以 10 再加上下一位 1，然后再除以 12，结果如下：

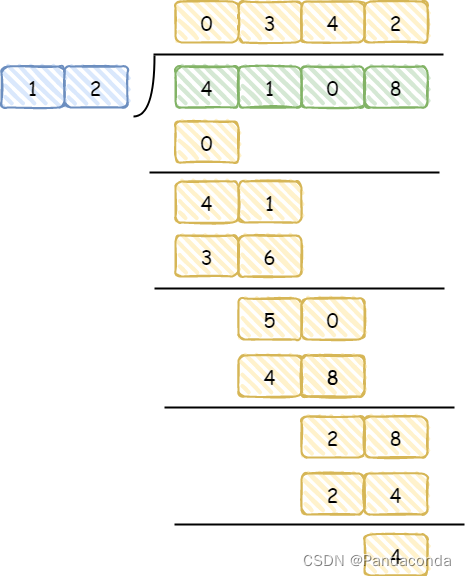
我们在代码实现的时候其实也是按照这样的过程实现，所以会出现前导 0 的问题，需要计算完之后解决，废话少说直接上步骤：

跟高精度乘法操作一样，只需将一个数用字符串接收即可，另一个数用整型类型接收，然后将字符串转换成数字传入到数组 A 当中，注意这里仍然是数字的低位放到数组下标的低位。
然后开始计算操作，上面提到，除法操作和加减乘操作不同，它是直接从数字的高位开始运算，但由于我们是逆序传入数组的，所以在运算的时候是从 A.size-1 这一个下标往前开始运算（参考代码部分），我们还是拿上面的 4108 / 12 进行举例，观察具体是如何实现的。这里为了区分加减乘，我们用的附加位是 r，用来保存余数并用于下一步的计算。

可以发现，第一个数 4 不够 12 除，所以 C 中推入的结果为 0，再来看下一步。

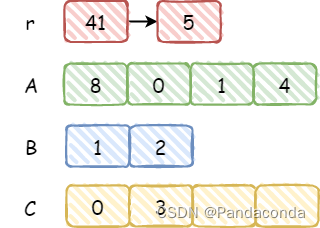
按照除法运算规则，上一步除完的余数需要乘以 10 然后加上下一位，即 r=4*10+1=41，这时候发现够除了，故将 41/12=3 推入 C 中，然后将 r 更新为 41%12=5，可以发现这和我们上面的手动运算过程几乎一模一样，然后再看下一步。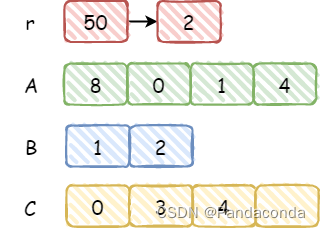

和上一步一样，可以得到 r=5*10+0=50，故将 50/12=4 推入 C 中，然后将 r 更新为 50%12=2。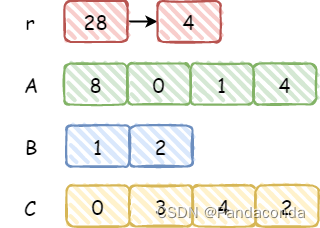

同上，可以得到 r=2*10+8=28，故将 28/12=2 推入 C 中，这时候发现已经除完了，但是发现 C 出现了前导 0，为了操作方便，我们先将数组 C 反转一下，然后再通过 while 循环将多余的 0 给 pop_back 出去（参考代码部分），最后返回 C 以及余数。
由于处理的时候需要去掉前导 0，故返回的数组仍然是倒过来的，所以将 C 逆序输出就是最终答案，当然余数也要一起输出。

#include<bits/stdc++.h>
using namespace std;

//高精度除法
vector<int> Div(vector<int> a, int b, int& r)
{
    vector<int> c;
    for (int i = a.size() - 1; i >= 0; i--)
    {
        r = r * 10 + a[i];
        c.push_back(r / b);
        r %= b;
    }
    reverse(c.begin(), c.end());
    //去除多余的0
    while (c.size() > 1 && c.back() == 0)  c.pop_back();
    return c;
}

int main()
{
    string a;
    int b;
    cin >> a >> b;
    vector<int> A;
    //将字符转换成数字
    for (int i = a.size() - 1; i >= 0; i--)
    {
        A.push_back(a[i] - '0');
    }
    int r = 0;
    vector<int> c = Div(A, b, r);
    for (int i = c.size() - 1; i >= 0; i--)
    {
        cout << c[i];
    }
    cout << endl << r << endl;
}

总结

恭喜您成功点亮高精度算法技能点！

整篇文章看下来可以发现，其实高精度的运算并不难，不要被它的外表所吓住，其中高精度加减乘法运算比较类似，它们都是从数字的低位开始运算，因为涉及到了进位和借位的操作；而高精度除法运算则相对难一点，它是从高位开始运算的。

高精度加法在运算完之后，如果附加位 t 不为 0，要记得加到数组 C 中；高精度减乘除运算完后，都涉及到了去除 0 的操作，其中减法是因为我们代码模拟时是用数组模拟，故高位进行减法操作后，可能会出现前导 0 的情况。而乘法则是可能出现乘数为 0 的情况，这时候进行运算会出现多个 0，但结果最多只能输出一个 0。而除法操作我们上面也看到了，如果一开始被除数不够时会填 0，这也是最后需要删除的。

还有就是加法和减法运算函数传入的都是两个数组，而乘法和除法运算函数传入的是一个数组和一个整数。

另外，重要的事情多说几遍，一定要记住在字符串转换成数字传入数组中时，低位数字对应在数组下标的低位！