题目

题目：https://leetcode.cn/problems/edit-distance/description/
类似题目：[leetcode 583] 两个字符串的删除操作

在这里插入图片描述

解法

动态规划

这题应该是字符串dp的终极形态了吧🤣，不看答案完全不会…看了答案发现原来还是dp…

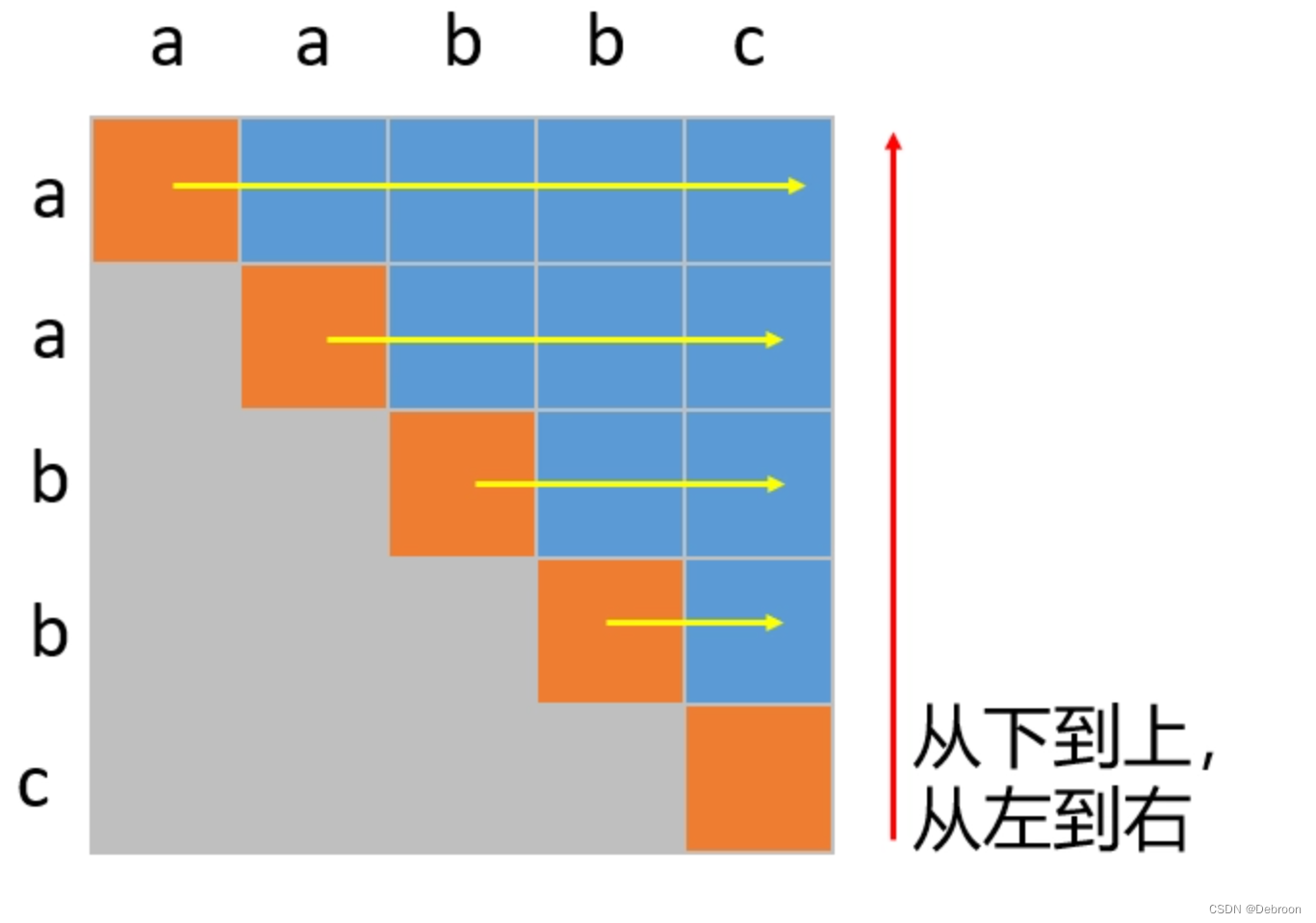
以例题为例，

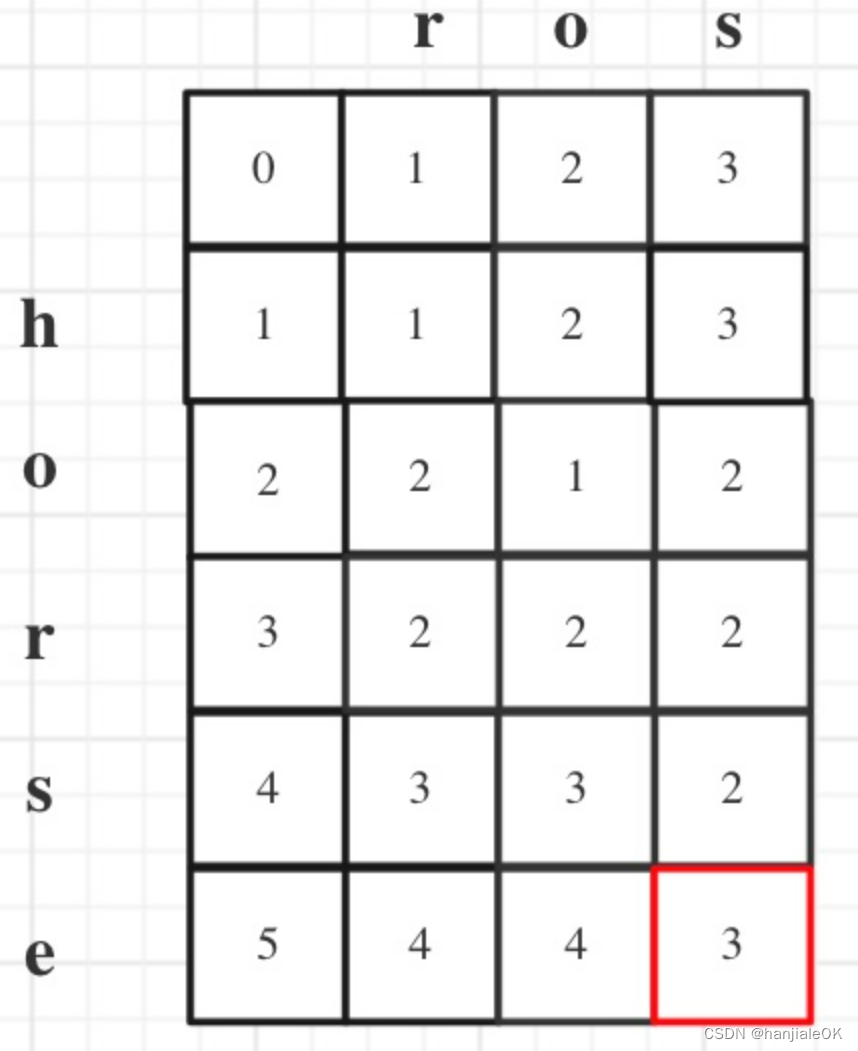
在这里插入图片描述

使用 dp[i][j] 表示 horse 的前 i 个字符变换城 ros 的前 j 个字符所需要的最少操作数。

如果 horse[i-1] == ros[j-1]，那么 dp[i][j] = dp[i-1][j-1]。比如 horse[i-1] = ros[j-1] = 's' 时，dp[i-1][j-1] 已经表示 hor 变成 ro 的最少操作数目，因此 dp[i][j] 无需增加。

如果 horse[i-1] != ros[j-1]，我们可以做3种操作：插入，删除，替换

插入：比如 horse[i-1] = 'e'， ros[j-1] = 's' 时，dp[i][j-1] 已经表示 horse 变成 ro 的最少操作数目，horse 想要变成 ros，只需要增加一个 s 即可，因此 dp[i][j] = dp[i][j-1]+1。
删除：比如 horse[i-1] = 'e'， ros[j-1] = 's' 时，dp[i-1][j] 已经表示 hors 变成 ros 的最少操作数目，horse 想要变成 ros，只需要删除 e 即可，因此 dp[i][j] = dp[i-1][j]+1。
替换：比如 horse[i-1] = 'e'， ros[j-1] = 's' 时，dp[i-1][j-1] 已经表示 hors 变成 ro 的最少操作数目，horse 想要变成 ros，只需要把 e 替换为 s 即可，因此 dp[i][j] = dp[i-1][j-1]+1。

熟记 dp[i][j] 的含义，上面的就很好理解了。

下面就是初始化的问题

在这里插入图片描述

空字符串变为空字符串无需操作，horse 变为空字符串需要删除5次，空字符串变为 ros 需要插入3次。

最终代码如下

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.length();
        int n = word2.length();
        vector<vector<int>> dp(m+1, vector<int>(n+1, 0));
        for (int i = 1; i <= m; i++) {
            dp[i][0] = i;
        }
        for (int j = 1; j <= n; j++) {
            dp[0][j] = j;
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1[i-1] == word2[j-1]) {
                    dp[i][j] = dp[i-1][j-1];
                }
                else {
                    dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1])) + 1;
                }
            }
        }
        return dp[m][n];
    }
};