877. 石子游戏

• • 题目
  • 算法设计：奇偶
  • 算法设计：动态规划

 

---

题目

 

---

算法设计：奇偶

最简单的情况，只有2堆石子（石子奇数），先稳赢。

但是四堆情况不同了，如 [3 7 2 3]。

不能直接选最大的，只能选数组开头和末尾。

那我们就按照取法的顺序，把 3 7 2 3 分成 2 组，偶数组 7 3，和奇数组 3 2。

• 如 3 7 2 3，先手要赢，必须取到 7，怎么可以取到 7 呢？
• 7 是奇数，就取奇数组，7 是偶数，就取偶数组，因为奇数、偶数必然有一个更大，先手必然赢。
• 先手取第一个（奇数），后手只能取第二、四个（偶数），继续维持奇偶性质即可
• 先手取第四个（偶数），后手只能取第一、三个（奇数），继续维持奇偶性质即可

因为石子是奇数，堆数是偶数，取法只能是数组开头和结尾，你的取法要么是奇数组，要么是偶数组。

那么只需要计算出，哪个组大，先手就取哪个组即可。

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        return true;       // 先手必赢
    }
};

 

---

算法设计：动态规划

官方的题解的状态是这样定义的: dp(i, j) 为先手可以获得的最大分数，初看这个状态很正确，实际是一个非常明显的错误.

因为当我们考虑 dp(i, j) 由 dp(i + 1, j) 转移过来时，即取了头部下标为i的这个数, 然后我们来看 dp(i + 1, j) 这个状态，按照官方的定义 dp(i + 1, j) 这个状态为 Alice 可以获得的最大分数，这里显然是错误的，因为 dp(i + 1, j) 这个状态不是 Alice。

那么正确的状态定义应该是啥?

• 答案是从区间 [L, R] 这个状态，先手和后手最大石子差。

这个状态是不是看起来很简单，而且可能会有很多人疑问，这个状态的 id 怎么没有记录，是 A，还是 B 到达了这个状态呢？

其实这就是这类问题的关键：因为是两个人在博弈，所以从当前状态转移到下一个状态时，就体现了 id 的变化，比如说当前状态是A，因为是两个人在玩，下一个状态就是B，这里很关键。

为什么状态定义为二维 dp[i][j]，因为这题和子序列问题一样，是不连续的序列，通常需要俩个指针来定位，如下表：

i	i+1					j-1	j
5	3	4	6	1	6	5	7

分析，最大石子差 f[i][j] 从哪里来？

• 从左端拿，先手拿 piles[i]，后手从 f[i+1][j] 的俩端中选出最大值，双方石子差为 piles[i] - f[i+1][j]，结果为正，说明先手赢

• 从右端拿，先手拿 piles[j]，后手从 f[i][j-1] 的俩端中选出最大值，双方石子差为 piles[j] - f[i][j-1]，结果为负，说明后手赢

• 状态转移方程：$f[i][j]=max(piles[i]-f[i+1][j],piles[j]-f[i][j-1])$

代码实现：

• 状态转移方向：想计算出 f[i][j] 就需要知道 f[i][j-1]、f[i+1][j]。
• 最简单情况：那 f[i][j-1]、f[i+1][j] 怎么计算出来？最简单的情况是，下图的初始化。
  
• 循环遍历方向：为了保证计算 f[i][j] 时，f[i][j-1]、f[i+1][j] 已经计算出来，循环遍历为：

斜着遍历：

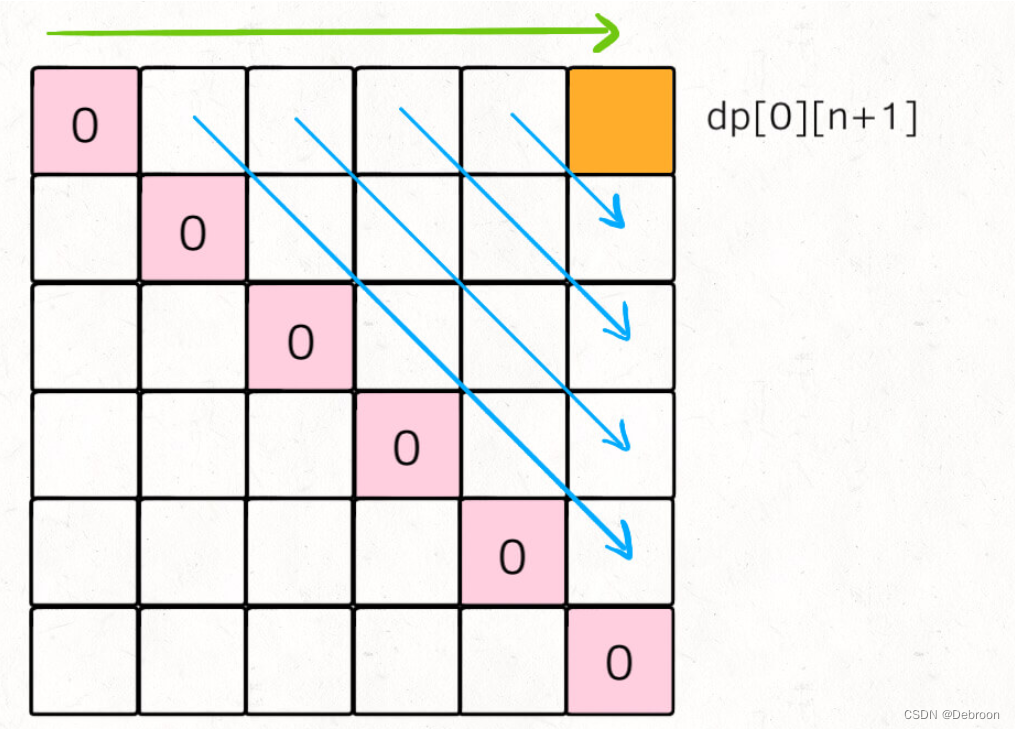
或者，反着遍历：

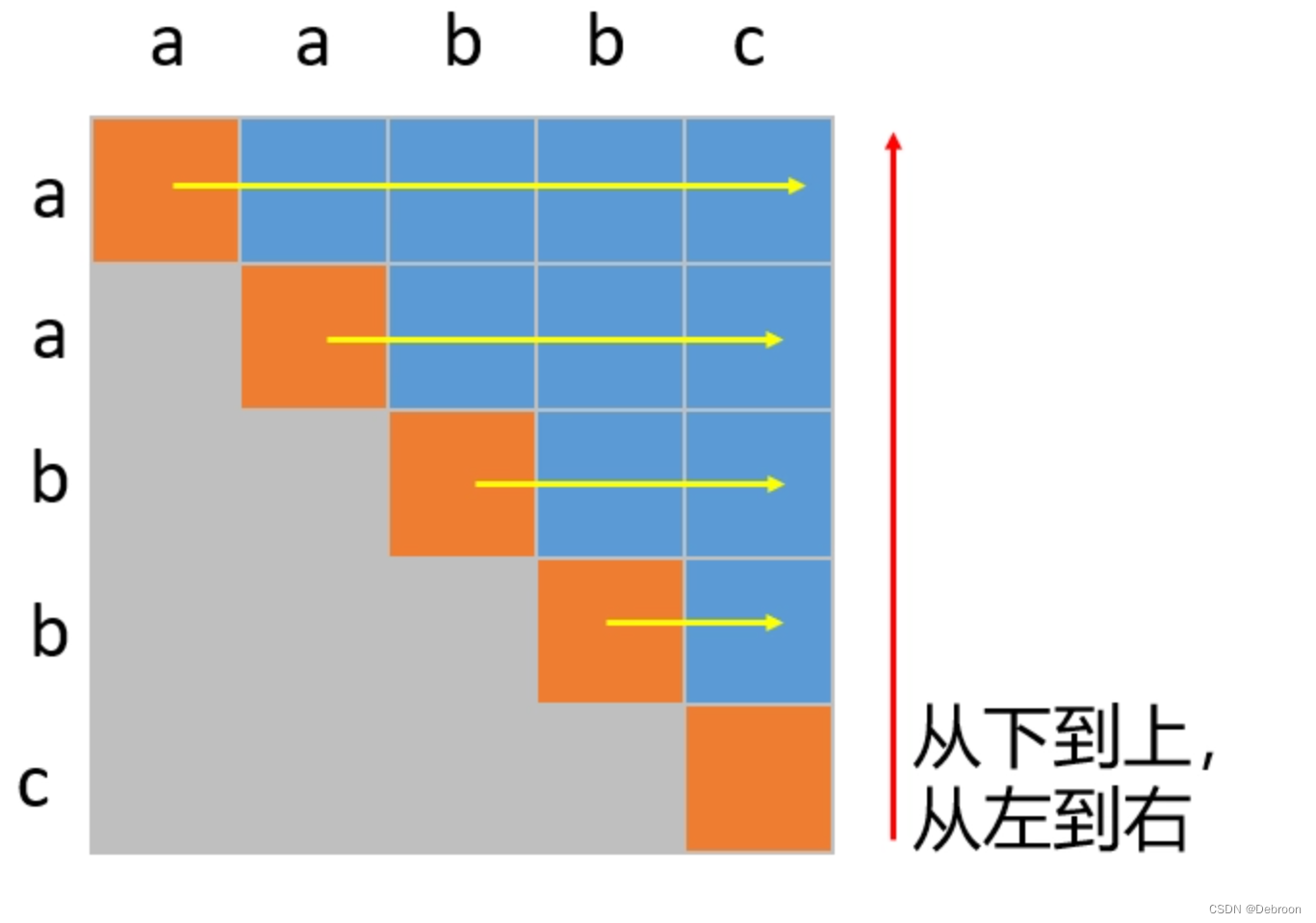
class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int n = piles.size();
        vector<vector<int>> f(n, vector<int>(n));
        for (int i = 0; i < n; i++)               // 最简单的情况
            f[i][i] = piles[i];
        for (int i = n - 1; i >= 0; i--)          // 反着遍历
            for (int j = i + 1; j < n; j++) {
                int a = piles[i] - f[i + 1][j];
                int b = piles[j] - f[i][j - 1];
                f[i][j] = max(piles[i] - f[i + 1][j], piles[j] - f[i][j - 1]);
            }
        return f[0][n - 1] > 0;                   // 正数，先手赢
    }
};