平均数,加权平均数,中位数,众数
1、平均数:所有数加在一起求平均
2、中位数:对于有限的数集,可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个,通常取最中间的
两个数值的平均数作为中位数。
3、众数:出现次数最多的那个数
4、加权平均数:加权平均值即将各数值乘以相应的权数,然后加总求和得到总体值,再除以总的单位数。加权平均值的大小不仅取决于
总体中各单位的数值(变量值)的大小,而且取决于各数值出现的次数(频数),由于各数值出现的次数对其在平均数中的影响起着权衡
轻重的作用,因此叫做权数。 因为加权平均值是根据权数的不同进行的平均数的计算,所以又叫加权平均数。在日常生活中,人们常常
把“权数”理解为事物所占的“权重”
x占a% y占b% z占c% n占m%
加权平均数=(ax+by+cz+mn)/(x+y+z+n)
一维数组
沿轴向进行计算,一维数组只有一个0轴
import numpy as np
a = np.array([1,2,3,4,3,5,3,6])
print(f'数组:{a}')
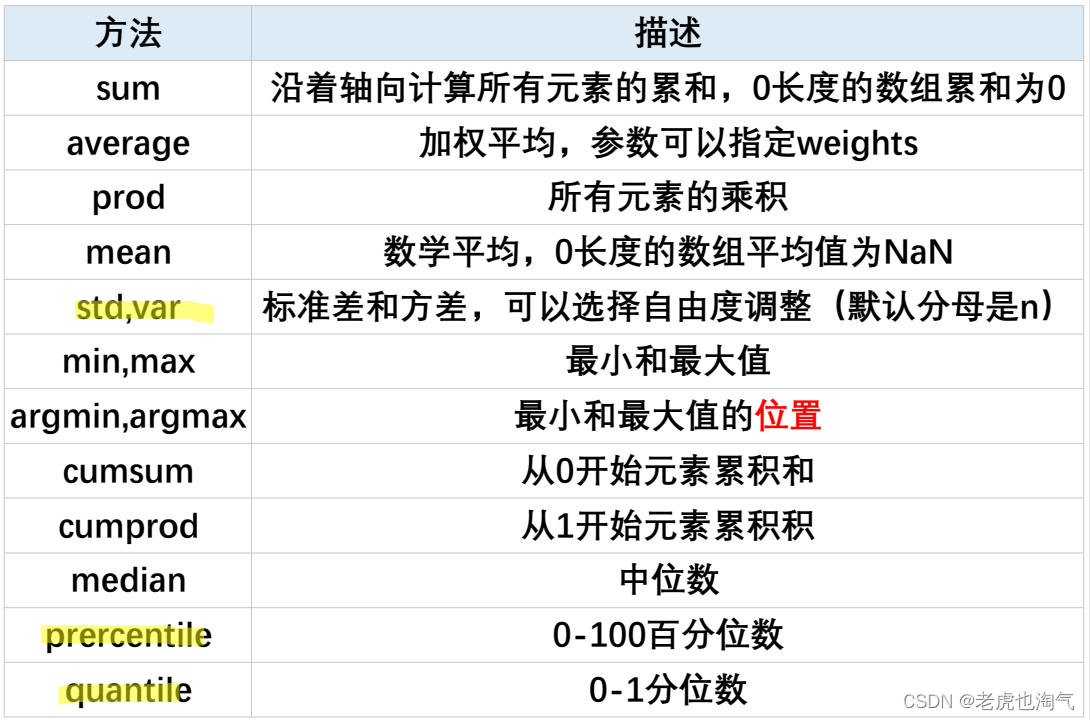
print(np.sum(a))
print(np.prod(a))
print(np.cumsum(a)) # 从0开始元素的累积和
print(np.cumprod(a)) # 从1开始元素的累积积
print(np.max(a))
print(np.min(a))
print(np.argmax(a)) # 最大值所在的下标
print(np.argmin(a)) # 最小值所在的下标
print(np.mean(a)) # 平均数
print(np.median(a)) # 中位数
print(np.average(a)) # 加权平均
counts = np.bincount(a) # 统计非负整数的个数,不能统计浮点数
print(np.argmax(counts)) # 返回众数,此方法不能用于二维数组
Numpy中没有直接的方法求众数,但是可以这样实现:
import numpy as np
# bincount():统计非负整数的个数,不能统计浮点数
counts = np.bincount(nums)
#返回众数
np.argmax(counts)
二维数组
import numpy as np
from scipy import stats
a = np.array([[1,3,6],[9,2,3],[2,3,3]])
print(f'数组:\n{a}')
print('-'*30)
print(np.sum(a))
print(np.prod(a))
print(np.cumsum(a)) # 从0开始元素的累积和,返回一维数组
print(np.cumprod(a)) # 从1开始元素的累积积,返回一维数组
print(np.max(a))
print(np.min(a))
print(np.argmax(a))
print(np.argmin(a))
print(np.mean(a))
print(np.median(a))
print(np.average(a))
注意:数组的众数不建议在Numpy里面计算,在Pandas里面计算更简单。
将一维数组转成Pandas的Series,然后调用mode()方法
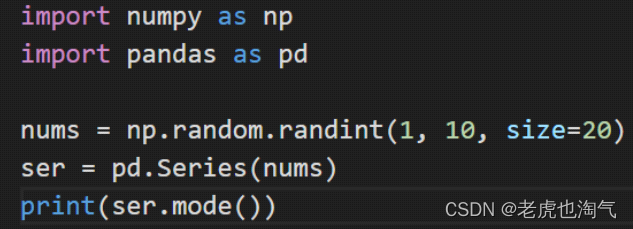
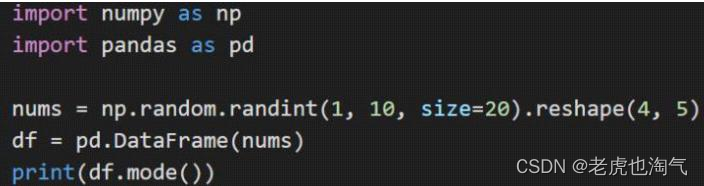
将二维数组转成Pandas的DataFrame,然后调用mode()方法
Numpy的axis参数的用途
axis=0代表行,axis=1代表列
所有的数学和统计函数都有这个参数,都可以使用
我们想按行或按列使用时使用这个参数
import numpy as np
a = np.array([[1,3,6],[9,3,2],[1,4,3]])
print(f'数组:\n{a}')
print('-'*30)
print(np.sum(a,axis=0)) # 每行中的每个对应元素相加,返回一维数组
print('-'*30)
print(np.sum(a,axis=1)) # 每列中的每个元素相加,返回一维数
其中思路正好是反的:axis=0 求每列的和。axis=1求每行的和。
• 行:每行对应一个样本数据
• 列:每列代表样本的一个特征
数组对应到现实中的一种解释:
• 对于机器学习、神经网络来说,不同列的量钢是相同的,收敛更快。
• 有两个特征,一个是商品单价1元至50元,另一个是销售数量3千个至1万个,这两个数字不可比,所以需要都做标准化。
• 比如在Excel里,单价一个列,销售数量一个列,不同列代表不同特征,所以用axis=0做计算
• 标准化一般使用:通过均值和方差实现
数组 = (数组 - mean(数组,axis=0))/ std(数组, axis=0)