如果你有一定神经网络的知识基础,想学习GAN生成对抗网络,可以按顺序参考系列文章:
深度学习 自动编码器与生成模型
深度学习 GAN生成对抗网络-1010格式数据生成简单案例
深度学习 GAN生成对抗网络-手写数字生成
一、前言
在前面一篇文章,我们使用GAN网络生成了1010格式的数字,接下来我们将使用GAN网络生成手写数字图像。本文不会一下给出最终方案,而是顺着思路一步步测试改良,加强大家的理解,最终达到我们想要的效果。
参考前面的代码架构,我们只需要作些许修改就行了:
1、使用MNIST手写数字数据集作为真实数据,输入鉴别器训练,鉴别器输入层节点数为28*28=784。
2、构造生成器神经网络,输出层节点数为784,即输出一张手写数字图片的数据。
3、对神经网络进行改良以达到更好的输出效果,如使用BCE损失、LeakyReLU激活函数、Adam优化器以及分层标准化等。
二、案例实战
我们先引入依赖库:
import matplotlib.pyplot as plt
import pandas
import torch
import torch.nn as nn
from torchvision import datasets,transforms
from torch.utils.data import DataLoader
2.1 真实数据源
加载数据集,如果不存在则自动下载:
# 加载数据集训练
train_data = datasets.MNIST(root="./data",train=True,transform=transforms.ToTensor(),download=True)
# 创建加载器,批次大小为1,不打乱数据
train_loader = DataLoader(train_data,batch_size=1,shuffle=False)
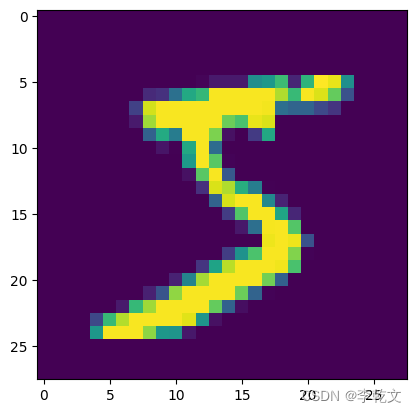
#显示第1张数字图像
plt.imshow(train_data.data[0])
2.5 构造鉴别器
鉴别器实际上是一个分类神经网络,跟1010数据生成GAN网络中的鉴别器差不多,只是神经网络大小不一样,其他都一样,如下:
self.model = nn.Sequential(
nn.Linear(784, 200),
nn.Sigmoid(),
nn.Linear(200, 1),
nn.Sigmoid()
)
完整的鉴别器:
#鉴别器
class Discriminator(nn.Module):
def __init__(self):
# 初始化Pytorch父类
super().__init__()
# 定义神经网络层
self.model = nn.Sequential(
nn.Linear(784, 200),
nn.Sigmoid(),
nn.Linear(200, 1),
nn.Sigmoid()
)
# 创建损失函数,使用均方误差
self.loss_function = nn.MSELoss()
# 创建优化器,使用随机梯度下降
self.optimiser = torch.optim.SGD(self.parameters(), lr=0.01)
# 训练次数计数器
self.counter = 0
# 训练过程中损失值记录
self.progress = []
# 前向传播函数
def forward(self, inputs):
return self.model(inputs)
# 训练函数
def train(self, inputs, targets):
# 前向传播,计算网络输出
outputs = self.forward(inputs)
# 计算损失值
loss = self.loss_function(outputs, targets)
# 累加训练次数
self.counter += 1
# 每10次训练记录损失值
if (self.counter % 10 == 0):
self.progress.append(loss.item())
# 每10000次输出训练次数
if (self.counter % 10000 == 0):
print("counter = ", self.counter)
# 梯度清零, 反向传播, 更新权重
self.optimiser.zero_grad()
loss.backward()
self.optimiser.step()
# 绘制损失变化图
def plot_progress(self):
df = pandas.DataFrame(self.progress, columns=['loss'])
df.plot(ylim=(0, 1.0), figsize=(16,8), alpha=0.1, marker='.', grid=True, yticks=(0, 0.25, 0.5))
2.4 测试鉴别器
这里我们也检验一下鉴别器,是否能将真实数据与随机数据区分开。
构造随机数生成函数
#返回size大小的0~1随机值
def generate_random(size):
random_data = torch.rand(size)
return random_data
print(generate_random(784).shape)
结果:
torch.Size([784])
训练
分别使用真实数据与随机数据训练鉴别器:
D = Discriminator()
for step, (images, labels) in enumerate(train_loader):
# 将图像数据重构为一维,由于加载器批次大小为1,所以只有一张图像
image_data_tensor=images.view(-1)
# 使用真实数据训练鉴别器
D.train(image_data_tensor, torch.FloatTensor([1.0]))
# 使用随机数据训练鉴别器
D.train(generate_random(784), torch.FloatTensor([0.0]))
结果:
counter = 10000
counter = 20000
counter = 30000
counter = 40000
counter = 50000
counter = 60000
counter = 70000
counter = 80000
counter = 90000
counter = 100000
counter = 110000
counter = 120000
有60000张真实图像,加上随机数据,共训练了120000次。
损失值变化
我们来看看训练过程中的鉴别器损失值变化:
D.plot_progress()
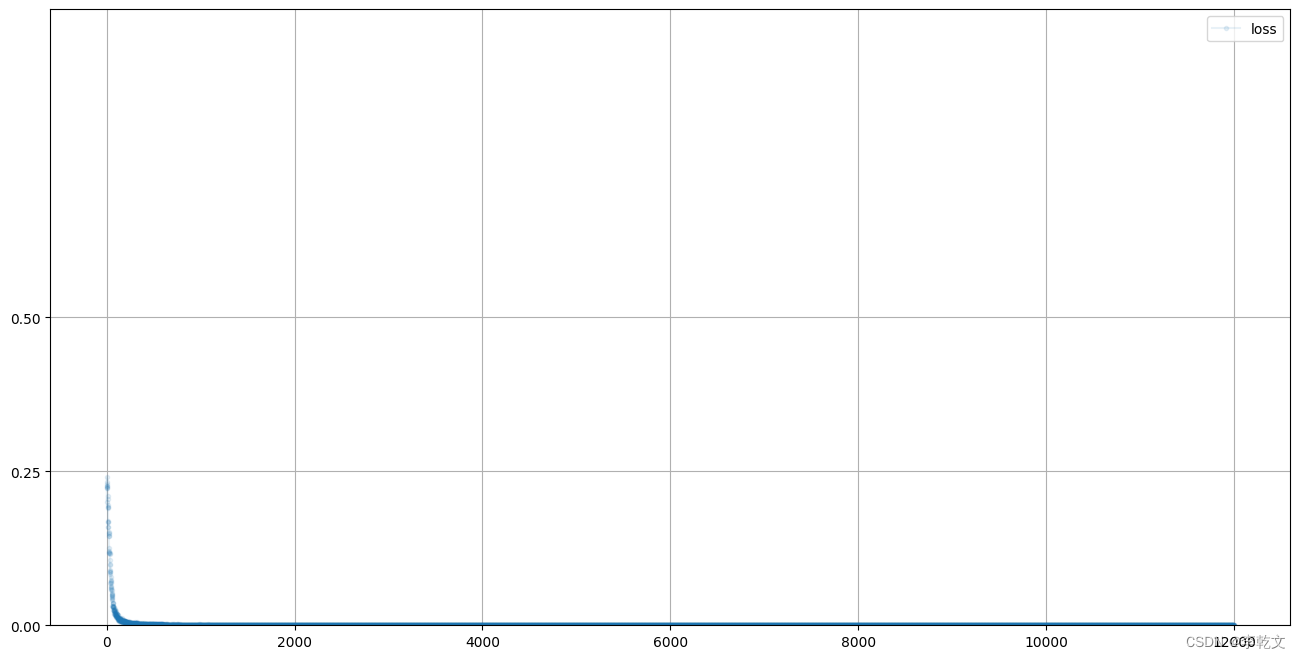
如上图所示,损失值一开始接近0.25,随着训练次数增加,损失值逐渐接近0。
鉴别效果
我们再来测试一下鉴定器的效果,现在分别输入1010格式数据与随机数据,代码和运行结果如下:
#随机选取训练集中图像、以及生成随机噪声图像,分别作为输入来测试训练后的鉴别器
import random
image_real=train_data.data[random.randint(0, 59999)].type(torch.FloatTensor).view(-1)
print(D.forward(image_real).item())
image_fake=generate_random(784)
print(D.forward(image_fake).item())
结果:
0.999976634979248
0.008260449394583702
得出的结果分别接近1和0,这说明鉴别器能够区分真实数据与随机噪声。
2.5 构造生成器
我们的生成器的输出层节点数需要与MNIST图像大小相同,即有784个输出值。也是跟1010数据生成GAN中的生成器差不多,神经网络大小不一样,其他都一样,如下:
self.model = nn.Sequential(
nn.Linear(1, 200),
nn.Sigmoid(),
nn.Linear(200, 784),
nn.Sigmoid()
)
完整的生成器:
# 生成器
class Generator(nn.Module):
def __init__(self):
# 初始化Pytorch父类
super().__init__()
# 定义神经网络层
self.model = nn.Sequential(
nn.Linear(1, 200),
nn.Sigmoid(),
nn.Linear(200, 784),
nn.Sigmoid()
)
# 注意这里没有损失函数,在训练时使用鉴别器的损失函数。
# 创建优化器,使用随机梯度下降
self.optimiser = torch.optim.SGD(self.parameters(), lr=0.01)
# 训练次数计数器
self.counter = 0
# 训练过程中损失值记录
self.progress = []
# 前向传播函数
def forward(self, inputs):
return self.model(inputs)
# 训练函数
def train(self, D, inputs, targets):
# 前向传播,计算网络输出
g_output = self.forward(inputs)
# 将生成器输出,传入鉴别器,输出分类结果
d_output = D.forward(g_output)
# 计算鉴别误差
loss = D.loss_function(d_output, targets)
# 累加训练次数
self.counter += 1
# 每10次训练记录损失值
if (self.counter % 10 == 0):
self.progress.append(loss.item())
# 梯度清零, 反向传播, 更新权重。注意这里是对鉴别器的误差进行反向传播,但只更新生成器的权重
self.optimiser.zero_grad()
loss.backward()
self.optimiser.step()
# 绘制损失变化图
def plot_progress(self):
df = pandas.DataFrame(self.progress, columns=['loss'])
df.plot(ylim=(0, 1.0), figsize=(16,8), alpha=0.1, marker='.', grid=True, yticks=(0, 0.25, 0.5))
2.6 检查生成器输出
现在我们检查一下生成器的输出图像:
G = Generator()
output = G.forward(generate_random(1))
img = output.detach().numpy().reshape(28,28)
plt.imshow(img)
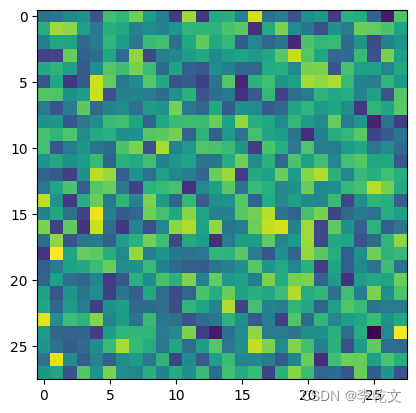
现在我们成功地生成了一张图像,由于现在没有对生成器进行训练,这张图像看起来像是一堆乱码。
2.7 训练GAN
训练
代码跟1010数据生成GAN几乎一样:
D = Discriminator()
G = Generator()
for step, (images, labels) in enumerate(train_loader):
image_data_tensor=images.view(-1)
# 使用真实数据训练鉴别器
D.train(image_data_tensor, torch.FloatTensor([1.0]))
# 用生成样本训练鉴别器
# 使用detach()以避免计算生成器G中的梯度
D.train(G.forward(generate_random(1)).detach(), torch.FloatTensor([0.0]))
# 训练生成器
G.train(D, generate_random(1), torch.FloatTensor([1.0]))
结果:
counter = 10000
counter = 20000
counter = 30000
counter = 40000
counter = 50000
counter = 60000
counter = 70000
counter = 80000
counter = 90000
counter = 100000
counter = 110000
counter = 120000
训练花了2m19.5s。
损失值变化
我们来看看鉴别器损失值的变化:
D.plot_progress()
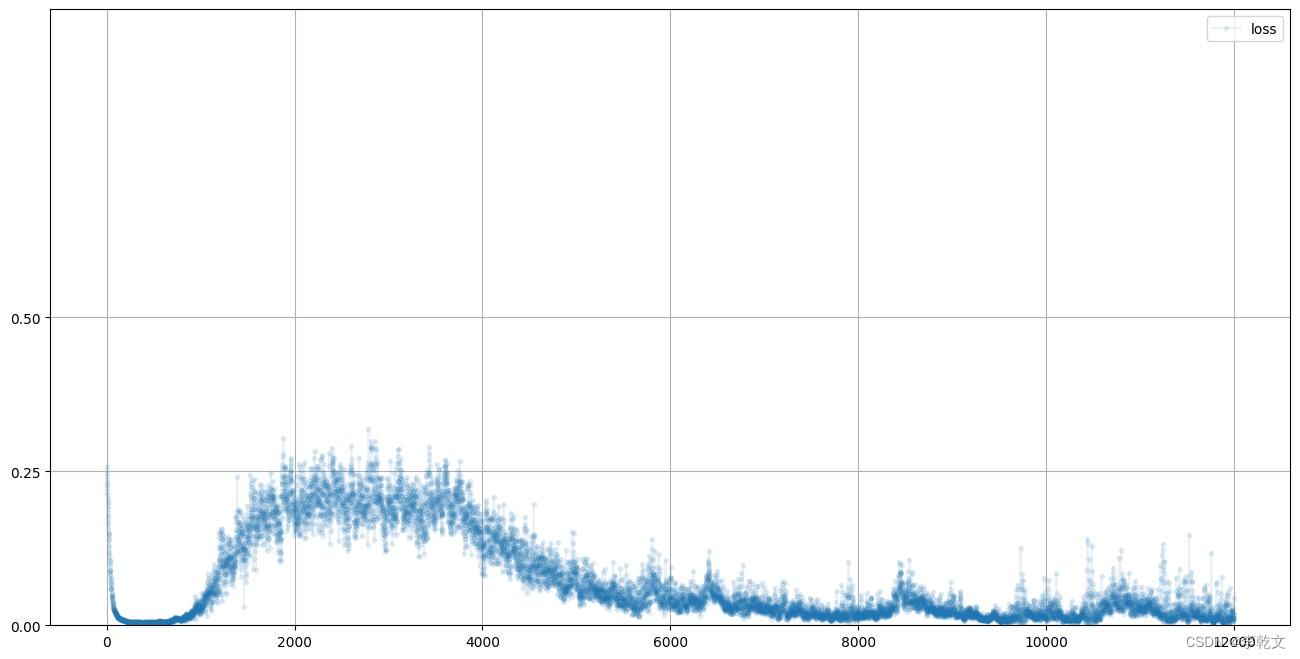
可以看到,鉴别器的损失值从0.25迅速降低到0并维持一段时间,表明此时鉴别器占上风;而后上升到0.25附近,表明鉴别器与生成器旗鼓相当;最后损失值又降低到较低水平,表明鉴别器再次领先生成器,生成器大概率没能骗过鉴别器。
再来看看生成器损失值的变化:
G.plot_progress()
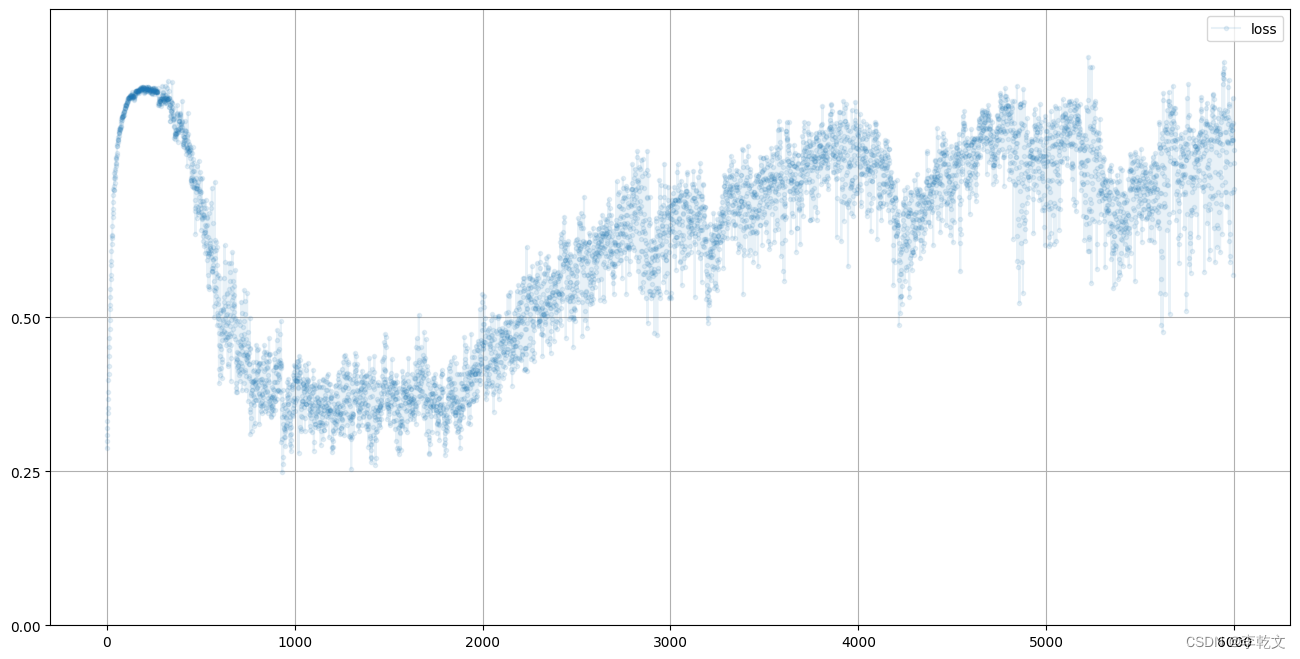
跟鉴别器是相反的。
生成数据
现在我们来看一下,用训练好的生成器生成的图像效果如何:
f, axarr = plt.subplots(2,3, figsize=(16,8))
for i in range(2):
for j in range(3):
output = G.forward(generate_random(1))
img = output.detach().numpy().reshape(28,28)
axarr[i,j].imshow(img, interpolation='none', cmap='Blues')
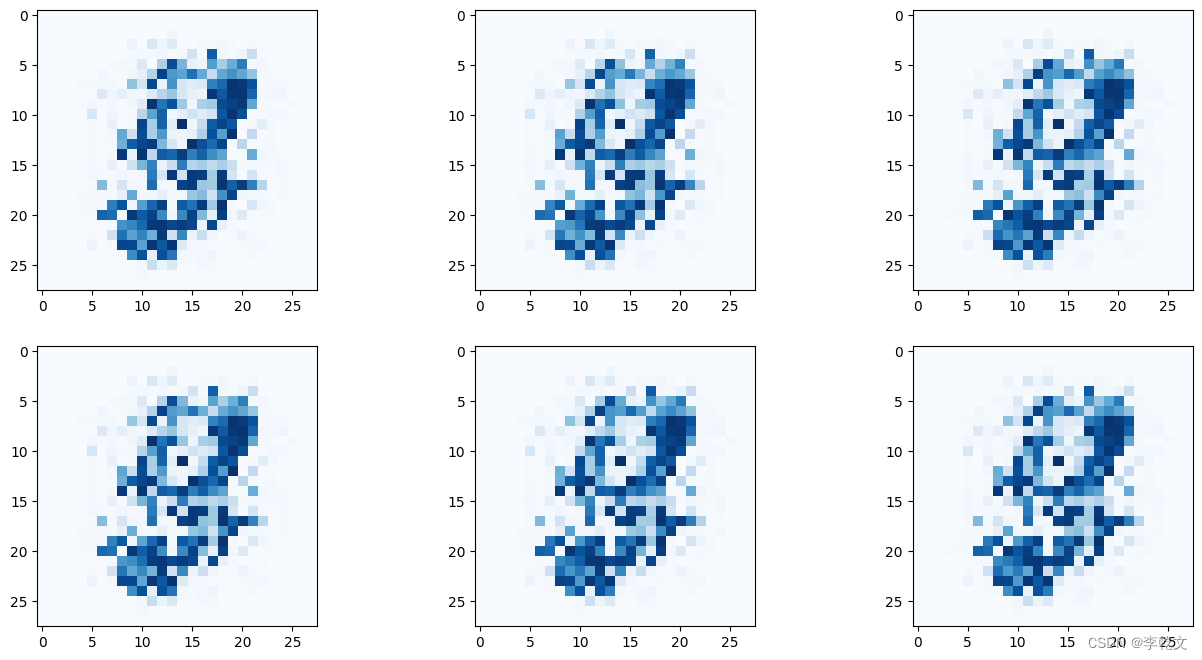
有点手写数字的样子,但不够清晰准确。但好歹我们用GAN生成了我们的手写数字,随着后续的优化改良,会达到更加完美的效果。
2.8 模式崩溃
奇怪的是,上面的6张图像肉眼看起来几乎是一模一样的。这种现象叫做模式崩溃,也叫模式坍塌(mode collapse),在GAN训练中非常常见。
目前这种现象还无法完全解释清楚,但是我们可以通过一些改良方法来解决上述的一些问题。
2.9 改良方法
损失函数
对于分类问题,损失函数使用二元交叉熵BCELoss()往往比均方误差MSELoss()效果更好。因为它能对正确分类进行奖励,而对错误分类进行惩罚。
由于生成器无需定义损失函数,所以我们只需要修改鉴别器的损失函数即可:
self.loss_function = nn.BCELoss()
激活函数与分层标准化
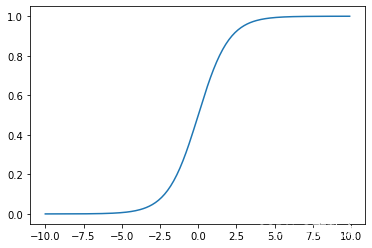
如上图所示,Sigmoid函数有个缺点,在输入值变得很大或变得很小时,梯度越来越小几乎消失。这会导致我们难以通过梯度来更新权重参数。
我们在中间层换成另外一种激活函数:LeakyReLU()函数。由于篇幅有限,此处就不展开了。
另外我们使用LayerNorm()函数对中间层输出值进行标准化,让它们均值为0,避免较大值引起的梯度消失。
修改之后,鉴别器网络层代码为:
self.model=nn.Sequential(
nn.Linear(784, 200),
nn.LeakyReLU(0.02),
nn.LayerNorm(200),
nn.Linear(200, 1),
nn.Sigmoid()
)
可能对于生成器来说,使用一个随机数作为输入,需要输出一张有784个像素的图像,这太难了,我们可以给生成器提供更多的随机数作为输入(此处定为100)。修改后生成器的网络层代码为:
self.model = nn.Sequential(
nn.Linear(100, 200),
nn.LeakyReLU(0.02),
nn.LayerNorm(200),
nn.Linear(200, 784),
nn.Sigmoid()
)
为什么最后的激活函数还是Sigmoid呢?因为我们这是一个分类任务,需要输出0~1的值。
优化器
我们把SGD改为Adam优化器来进行梯度下降,它利用动量的概念(想象一下小球利用动量滚过一个小坑),能减少陷入局部最小值的可能。其次它对每个学习的参数都使用单独学习率,且学习率会动态变化。在很多任务中,Adam优化器是首选。
鉴别器和生成器都需要修改:
self.optimiser = torch.optim.Adam(self.parameters(), lr=0.0001)
经过以上各种优化后,生成图片效果如下:
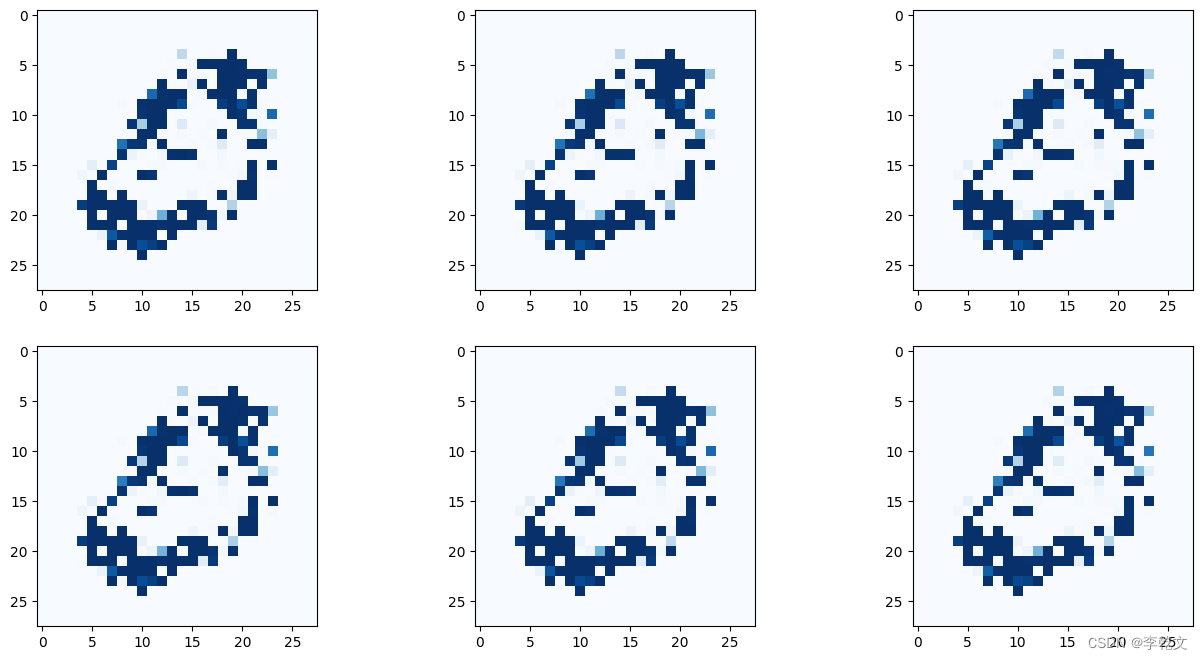
图片清晰了很多,结构也更像一个数字了,但是还是存在模式崩溃问题,我们继续改良。
正态分布
我们提供给生成器输入层的随机数是通过torch.rand()函数生成的,这些随机数均匀分布在0~1之间。
现在我们换一种模式,使用torch.randn()函数,从一个平均值为0、方差为1的正态分布中抽取随机数。
#返回size大小的均值为0,均方误差为1的随机数
def generate_random(size):
random_data = torch.randn(size)
return random_data
训练之后,生成图片效果如下:
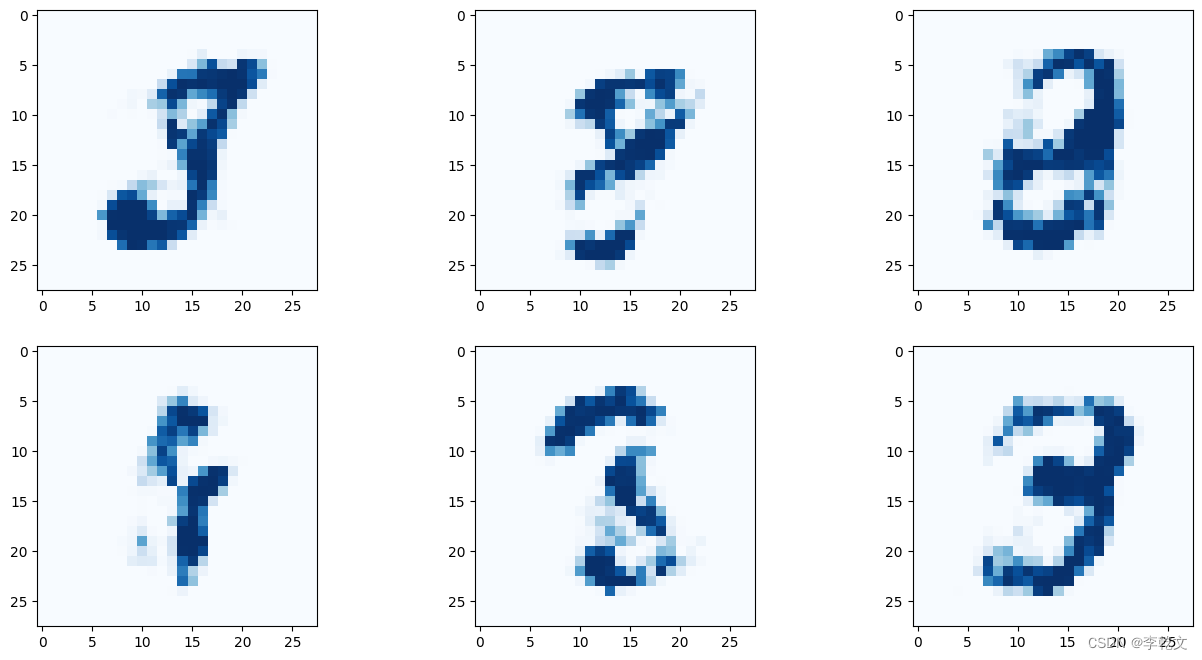
这时候我们惊奇地发现,模式崩溃问题竟然消失了!
不过生成的图片效果还是不尽人意,革命尚未成功,同志仍需努力!
增加训练周期
虽然我们解决了模式崩溃问题,不过图片质量还是有待提升。我们只能祭出不是办法的绝招——增加训练周期。比较耗时,但希望能有点效果吧。
这里我们把训练周期(epochs)设置为4:
D = Discriminator()
G = Generator()
#迭代次数
epochs=4
for epoch in range(epochs):
for step, (images, labels) in enumerate(train_loader):
image_data_tensor=images.view(-1)
# 使用真实数据训练鉴别器
D.train(image_data_tensor, torch.FloatTensor([1.0]))
# 用生成样本训练鉴别器
# 使用detach()以避免计算生成器G中的梯度
D.train(G.forward(generate_random(100)).detach(), torch.FloatTensor([0.0]))
# 训练生成器
G.train(D, generate_random(100), torch.FloatTensor([1.0]))
CPU终于跑不动了,经过漫长的等待。。。耗时19m25.2s,结果出来了!生成效果图如下:

效果还可以,大功告成!
如果你有更多的时间或者把代码修改在GPU上运行,可以尝试增加更多的训练周期可能效果会更好。
完整的GAN代码如下,不过还是希望大家能按照上面的思路走一遍,以便加深理解。
import matplotlib.pyplot as plt
import pandas
import torch
import torch.nn as nn
from torchvision import datasets,transforms
from torch.utils.data import DataLoader
# 加载数据集训练
train_data = datasets.MNIST(root="./data",train=True,transform=transforms.ToTensor(),download=True)
# 创建加载器,批次大小为1,不打乱数据
train_loader = DataLoader(train_data,batch_size=1,shuffle=False)
#返回size大小的均值为0,均方误差为1的随机数
def generate_random(size):
random_data = torch.randn(size)
return random_data
#鉴别器
class Discriminator(nn.Module):
def __init__(self):
super().__init__()
self.model=nn.Sequential(
nn.Linear(784, 200),
nn.LeakyReLU(0.02),
nn.LayerNorm(200),
nn.Linear(200, 1),
nn.Sigmoid()
)
# 定义损失函数
self.loss_function = nn.BCELoss()
# 创建优化器,使用Adam梯度下降
self.optimiser = torch.optim.Adam(self.parameters(), lr=0.0001)
# 计数器和进程记录
self.counter = 0
self.progress = []
def forward(self, inputs):
# 运行模型
return self.model(inputs)
def train(self, inputs, targets):
# 计算网络前向传播输出
outputs = self.forward(inputs)
# 计算损失值
loss = self.loss_function(outputs, targets)
# 每训练10次增加计数器
self.counter += 1
if (self.counter % 10 == 0):
self.progress.append(loss.item())
if (self.counter % 10000 == 0):
print("counter = ", self.counter)
#在反向传播前先把梯度归零
self.optimiser.zero_grad()
#反向传播,计算各参数对于损失loss的梯度
loss.backward()
#根据反向传播得到的梯度,更新模型权重参数
self.optimiser.step()
def plot_progress(self):
df = pandas.DataFrame(self.progress, columns=['loss'])
df.plot(ylim=(0, 1.0), figsize=(16,8), alpha=0.1,
marker='.', grid=True, yticks=(0, 0.25, 0.5, 1.0, 5.0))
# 生成器
class Generator(nn.Module):
def __init__(self):
# 初始化PyTorch父类
super().__init__()
# 定义神经网络层
self.model = nn.Sequential(
nn.Linear(100, 200),
nn.LeakyReLU(0.02),
nn.LayerNorm(200),
nn.Linear(200, 784),
nn.Sigmoid()
)
# 创建优化器,使用Adam梯度下降
self.optimiser = torch.optim.Adam(self.parameters(), lr=0.0001)
# 计数器和进程记录
self.counter = 0
self.progress = []
def forward(self, inputs):
# 运行模型
return self.model(inputs)
def train(self, D, inputs, targets):
# 计算网络输出
g_output = self.forward(inputs)
# 输入鉴别器
d_output = D.forward(g_output)
# 计算损失值
loss = D.loss_function(d_output, targets)
# 每训练10次增加计数器
self.counter += 1
if (self.counter % 10 == 0):
self.progress.append(loss.item())
# 梯度归零,反向传播,并更新权重
self.optimiser.zero_grad()
loss.backward()
#更新由self.optimiser而不是D.optimiser触发。这样一来,只有生成器的链接权重得到更新
self.optimiser.step()
def plot_progress(self):
df = pandas.DataFrame(self.progress, columns=['loss'])
df.plot(ylim=(0, 1.0), figsize=(16,8), alpha=0.1,
marker='.', grid=True, yticks=(0, 0.25, 0.5, 1.0, 5.0))
D = Discriminator()
G = Generator()
#迭代次数
epochs=4
# 训练GAN
for epoch in range(epochs):
for step, (images, labels) in enumerate(train_loader):
image_data_tensor=images.view(-1)
# 使用真实数据训练鉴别器
D.train(image_data_tensor, torch.FloatTensor([1.0]))
# 用生成样本训练鉴别器
# 使用detach()以避免计算生成器G中的梯度
D.train(G.forward(generate_random(100)).detach(), torch.FloatTensor([0.0]))
# 训练生成器
G.train(D, generate_random(100), torch.FloatTensor([1.0]))
# 保存模型
# torch.save(D, 'GAN_Digits_D.pt')
torch.save(G, 'GAN_Digits_G.pt')
#加载模型
G=torch.load('GAN_Digits_G.pt')
# 生成效果图
f, axarr = plt.subplots(2,3, figsize=(16,8))
for i in range(2):
for j in range(3):
output = G.forward(generate_random(100))
img = output.detach().numpy().reshape(28,28)
axarr[i,j].imshow(img, interpolation='none', cmap='Blues')
参考资料
《PyTorch生成对抗网络编程》(PS:写得太好了,强烈推荐。)