关系运算

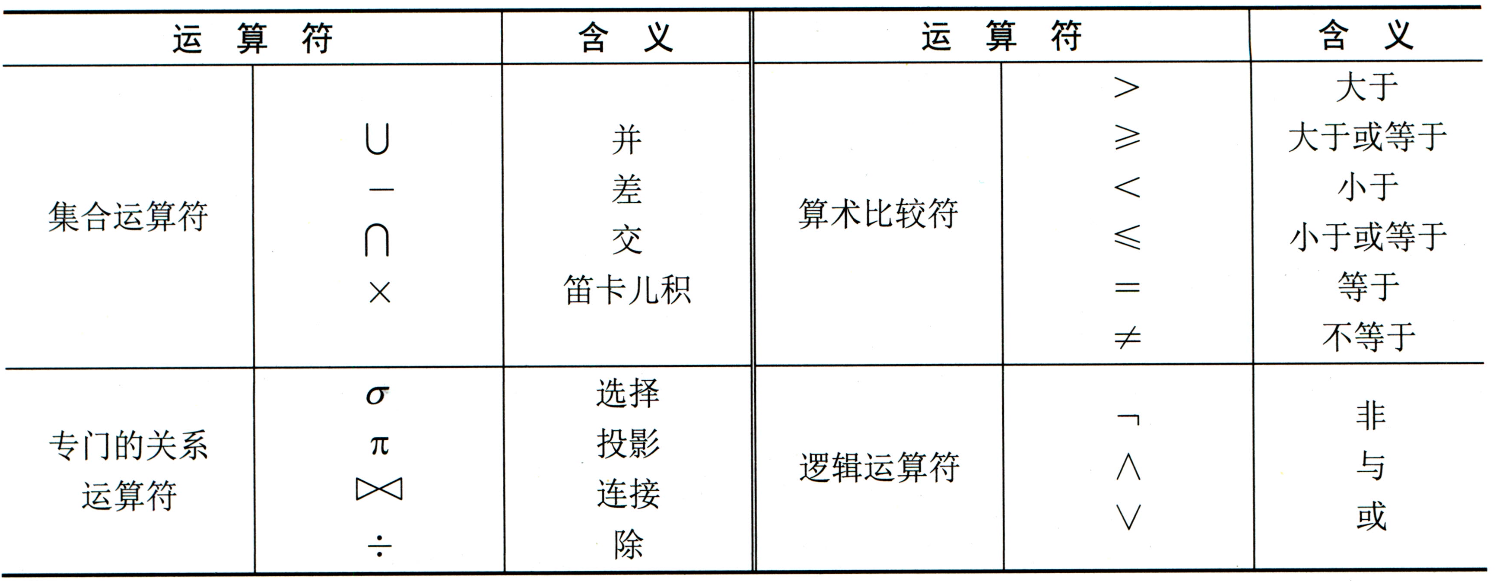
关系代数运算符有集合运算符、专门的关系运算符、算术比较符和逻辑运算符，如下：

并（Union）

关系R与S的并由属于R或属于S的元组构成的集合组成，定义为 R ∪ S = { t ∣ t ∈ R ∨ t ∈ S } R\cup S=\{t|t\in R \vee t\in S\} R∪S={t∣t∈R∨t∈S}，t为元组变量，R与S具有相同的关系模式（结构相同）。

等价SQL：

SELECT A,B,C FROM R
UNION 
SELECT A,B,C FROM S;

差（Difference）

关系R与S的差由属于R但不属于S的元组构成的集合组成，定义为 R − S = { t ∣ t ∈ R ∧ t ∉ S } R - S=\{t|t\in R \wedge t\notin S\} R−S={t∣t∈R∧t∈/S}，t为元组变量，R与S具有相同的关系模式（结构相同）。

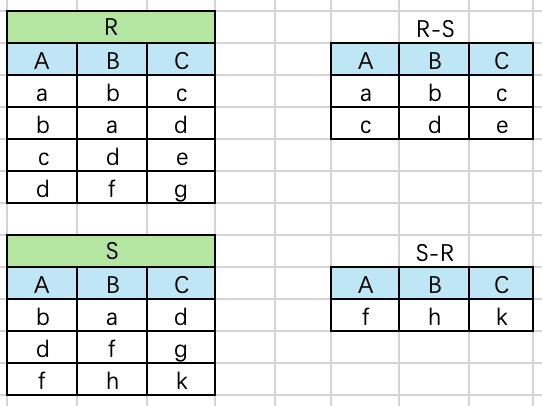
等价SQL：

SELECT A,B,C FROM R
EXCEPT
SELECT A,B,C FROM S;

交（Intersection）

关系R与S的差由属于R同时又属于S的元组构成的集合组成，定义为 R ∩ S = { t ∣ t ∈ R ∧ t ∈ S } R \cap S=\{t|t\in R \wedge t\in S\} R∩S={t∣t∈R∧t∈S}，t为元组变量，R与S具有相同的关系模式（结构相同）。也可以表示成$R\cap S=R-(R-S),或者R\cap S=S-(S-R)$。

等价SQL：

SELECT A,B,C FROM R
INTERSECT
SELECT A,B,C FROM S;

笛卡尔积（Extended Cartesian Product）

两个元数分别为n目和m目的关系R和S的广义笛卡尔积是一个(n+m)列的元组的集合。元组的前n列是关系R的一个元组，后m列是关系S的一个元组，形式定义 R × S = { t ∣ t = < t n , t m > ∧ t n ∈ R ∧ t m ∈ S } R \times S=\{t|t= < t^n,t^m > \wedge t^n\in R \wedge t^m \in S \} R×S={t∣t=<tn,tm>∧tn∈R∧tm∈S}。其中，$<t^n,t^m>$表示元组$t_n和t^m$拼接成的一个元组，t为元组变量。

若R有$K_1$个元组，S有$K_2$个元组，则R和S的广义笛卡尔积有$K_1\times K_2$个元组。

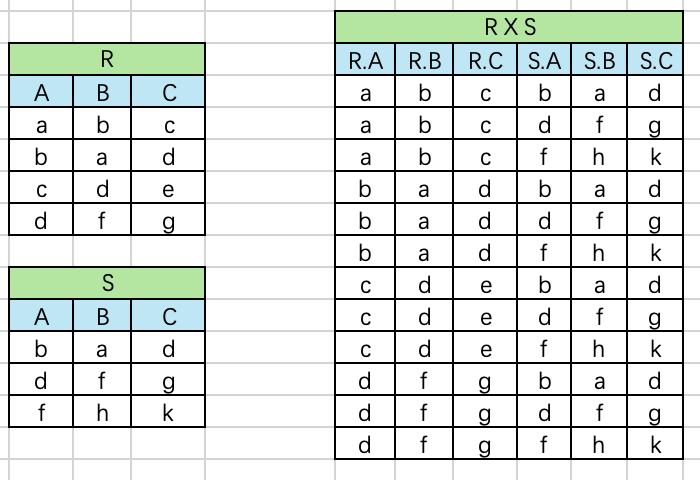
等价SQL：

SELECT * FROM R
CROSS JOIN S;

投影（projection）

投影是从垂直方向进行运算，在关系R中选择出若干属性列A组成新的关系，形式定义为 π A ( R ) = { t ∣ t [ A ] ∣ t ∈ S } \pi_A(R) =\{t|t[A]|t\in S\} πA​(R)={t∣t[A]∣t∈S}。

等价SQL：

SELECT A,C FROM R;

选择（Selection）

选择运算是从关系的水平方向进行运算，是从关系R中选择满足给定条件的诸元组，形式定义为 σ F ( R ) = { t ∣ t ∈ R ∧ F ( t ) = T r u e } \sigma_F(R)=\{t|t\in R \wedge F(t)=True\} σF​(R)={t∣t∈R∧F(t)=True}。

其中，F中的运算对象是属性名(或列的序号)或常数，运算符是算术比较符(<、≤、>、≥)和逻辑运算符($\wedge 、\vee 、-$)。例如，${\sigma }_{1\ge 6}(R)$表示选取R关系中第1个属性值大于等于第6个属性值的元组;${\sigma }_{1>6}(R)$表示选取R关系中第1个属性值大于6的元组。

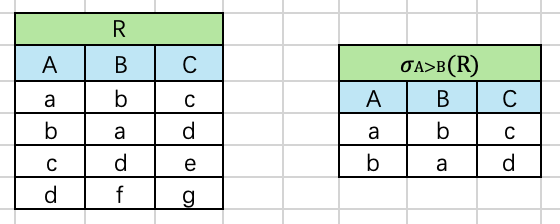
等价SQL：

SELECT A,B,C FROM R WHERE A>B;

除（Division）

除运算是同时从关系的水平方向和垂直方向进行运算。给定关系R(X,Y)和S(Y,Z)，X、Y、Z为属性组。$R÷S$应当满足元组在X上的分量值$x$的象集$Y_x$包含关系S在属性组Y上投影的集合。形式定义为 R ÷ S = { t n [ X ] ∣ t n ∈ R ∧ π y ( S ) ⊆ Y x R\div S=\{t_n[X]|t_n\in R \wedge \pi_y(S) \subseteq Y_x R÷S={tn​[X]∣tn​∈R∧πy​(S)⊆Yx​。

其中，$Y_x为x$在R的象集，$x=t_n[X]$。且$R÷S$的结果集的属性组为X。

示例：已知R和S的关系，求$R÷S$。

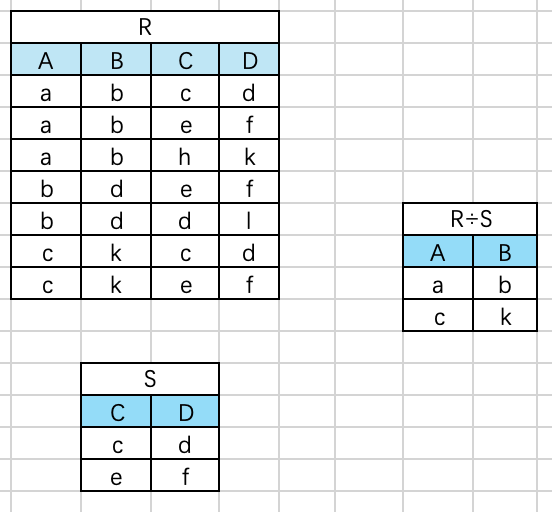
分析：根据定义，Y为属性CD，X为属性AB，$R÷S$应当满足元组在AB上的分量值$x$的象集$Y_x$包含关系S在属性组CD上投影的集合。关系S在Y上的投影为${\pi }_y(S)=\{(c,d),(e,f)\}$，属性组X(即AB)可以取3个值$\{(a,b),(b,d),(c,k)\}$

• $象集C{D}_{(a,b)}=\{(c,d),(e,f),(h,k)\}$。
• $象集C{D}_{(b,d)}=\{(e,f),(d,l)\}$。
• $象集C{D}_{(c,k)}=\{(c,d),(e,f)\}$。

由于上述象集包含${\pi }_y(S)有\{(a,b)\}和\{(c,k)\}$，所以$R÷S=\{(a,b),\{(c,k)\}$$

连接（join）

1. $\theta$连接

$\theta$连接是从R与S的笛卡尔积中选取属性间满足一定条件的元组，形式定义：

R ⋈ X θ Y S = { t ∣ t = < t n , t m > ∧ t n ∈ R ∧ t m ∈ S ∧ t n [ X ] θ t m [ Y ] } R \bowtie_{X\theta Y}S=\{t|t= < t^n,t^m > \wedge t^n \in R \wedge t^m \in S \wedge t^n[X] \theta t^m[Y]\} R⋈XθY​S={t∣t=<tn,tm>∧tn∈R∧tm∈S∧tn[X]θtm[Y]}

其中，$X\theta Y$为连接的条件，$\theta$是比较运算符，X和Y分别为R和S上度数相等，且可比的属性组。$t^n[X]$表示R中$t^n$元组的对应于属性X的一个分量。$t^n[Y]$表示R中$t^m$元组的对应于属性Y的一个分量。

还可以表示为$R{\bowtie }_{X\theta Y}S={\sigma }_{X\theta Y}(R\times S)$或者$R{\bowtie }_{i\theta j}S={\sigma }_{i\theta (i+j)}(R\times S)$。

等价SQL：

SELECT * FROM R
CROSS JOIN S
WHERE R.A<S.B;

2. 等值连接

当$\theta$为“=”时，称为等值连接，形式定义为 R ⋈ X = Y S = { t ∣ t = < t n , t m > ∧ t n ∈ R ∧ t m ∈ S ∧ t n [ X ] = t m [ Y ] } R \bowtie_{X= Y}S=\{t|t= < t^n,t^m > \wedge t^n \in R \wedge t^m \in S \wedge t^n[X] = t^m[Y]\} R⋈X=Y​S={t∣t=<tn,tm>∧tn∈R∧tm∈S∧tn[X]=tm[Y]}

3. 自然连接

自然连接时一种特殊的等值连接，要求两个关系中进行比较的分量必须是相同的属性组，并且在结果集中将重复属性去掉。形式定义：

R ⋈ S = { t ∣ t = < t n , t m ∗ > ∧ t n ∈ R ∧ t m ∈ S ∧ S . B 1 = R . B 1 ∧ R . B 2 = S . B 2 ∧ . . . ∧ R . B n = S . B n } R \bowtie_S=\{t|t= < t^n,t^{m^\ast} > \wedge t^n \in R \wedge t^m \in S \wedge S.B_1=R.B_1\wedge R.B_2=S.B_2\wedge ... \wedge R.B_n=S.B_n \} R⋈S​={t∣t=<tn,tm∗>∧tn∈R∧tm∈S∧S.B1​=R.B1​∧R.B2​=S.B2​∧...∧R.Bn​=S.Bn​}

其中$t_n$表示关系R的元组变量，$t_m$表示关系S的元组变量。R和S具有相同的属性组B，且$B=(B_1,B_2,...,B_k)$。假定R的属性为$A_1,A_2,...,A_{n-k},B_1,B_2,...,B_k$，假定S的属性为$B_1,B_2,...,B_k,B_{k+1},B_{k+2},...,B_m$，S的元组变量去除重复属性B所组成新的元组为$t^{m^{\ast }}$。

等价SQL：

SELECT R.A,R.B,R.C,R.D
FROM R,S 
WHERE R.A=S.A AND R.C=S.C;

要求两个关系中进行比较的分量必须是相同的属性组并且在结果集中将重复属性列去掉。

外连接（outer join）

外连接是连接运算的扩展，可以处理缺失的信息。

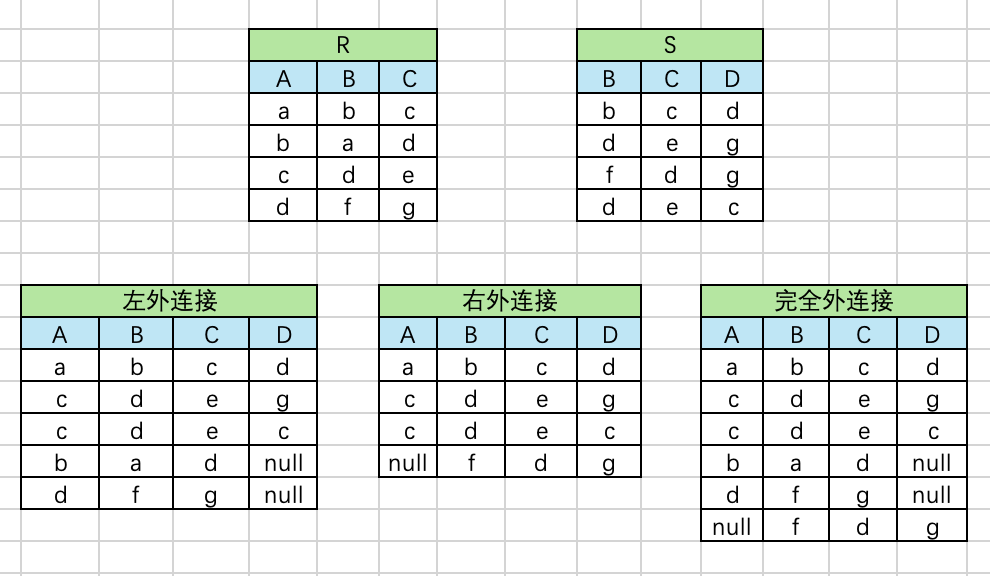
• 左外连接（left outer join）。取出左侧关系中所有与右侧关系中任一元组都不匹配的元组，用空值null填充所有来自右侧关系的属性。

等价SQL：

SELECT R.A,R.B,R.C,S.D
FROM R
LEFT JOIN S 
ON R.B=S.B AND R.C=S.C;

• 右外连接（right outer join）。取出右侧关系中所有与左侧关系中任一元组都不匹配的元组，用空值null填充所有来自左侧关系的属性。

等价SQL：

SELECT R.A,S.B,S.C,S.D
FROM R
RIGHT JOIN S 
ON R.B=S.B AND R.C=S.C;

• 完全外连接（full outer join）。完成左外连接和右外连接的操作。既填充左侧关系中所有与右侧关系中任一元组都不匹配的元组，又填充右侧关系中所有与左侧关系中任一元组都不匹配的元组，将产生的新元组加入自然连接的结果中。

等价SQL：

SELECT R.A,R.B,R.C,S.D
FROM R
LEFT JOIN S 
ON R.B=S.B AND R.C=S.C
UNION 
SELECT R.A,S.B,S.C,S.D
FROM R
RIGHT JOIN S 
ON R.B=S.B AND R.C=S.C;

聚集函数

聚集函数输入一个值的集合，返回单一值作为结果。如集合12,4,6,8,10,15}。将聚集函数sum用于该集合时返回和45；将聚集函数avg用于该集合时返回平均值7.5；将聚集函数count用于该集合时返回集合中元数的个数6；将聚集函数min用于该集合时返回最小值2；将聚集函数max用于该集合时返回最大值15。

元组演算

表现形式为 { t ∣ P ( t ) } \{t|P(t)\} {t∣P(t)}。其中，t是元组变量，$P(t)$ 是元组关系演算公式，公式是由原子公式组成的。

原子公式有如下三种形式：

1. $R(t)$。R是关系名，t是元组变量，表示命题为“t是关系R的一个元组”。
2. $t[i]\theta C或C\theta t[i]$。$t[i]$表示元组变量t的第i个分量，C是常量，$\theta$为算术比较运算符。表示命题为“元组变量t的第i个分量与C直接满足$\theta$运算“。如$t[3]{<}^{\prime }{8}^{\prime }$表示t的第三个分量小于8。
3. $t[i]\theta u[j]$。t、u是两个元组变量，表示命题为“元组变量t的第i个分量与元组变量u的第j个分量直接满足$\theta$运算”。如$t[2]\ge u[4]$表示t的第二个分量大于等于u的第四个分量。

若一个公式中的一个元组变量前有全称量词$\forall$或存在量词$\exists$符号，则称该变量为约束变量，否则称之为自由变量。公式可递归定义：

• 原子公式是公式。
• 如果是${\phi }_1$和${\phi }_2$公式，那么，$\neg {\phi }_1、{\phi }_1\vee {\phi }_2、{\phi }_1\wedge {\phi }_2、{\phi }_1\Rightarrow {\phi }_2$ 也都是公式。分别表示命题：$\neg {\phi }_1$表示“${\phi }_1$不是真“；${\phi }_1\vee {\phi }_2$表示“${\phi }_1$或${\phi }_2$或${\phi }_1和{\phi }_2$为真”；${\phi }_1\wedge {\phi }_2$表示“${\phi }_1$和${\phi }_2$都为真”；${\phi }_1\Rightarrow {\phi }_2$表示“若${\phi }_1$为真则${\phi }_2$为真”。
• 如果是${\phi }_1$公式，那么，$\exists t({\phi }_1)$是公式。表示命题为“若有一个t使${\phi }_1$为真，则$\exists t({\phi }_1)$为真，否则$\exists t({\phi }_1)$为假”。
• 如果是${\phi }_1$公式，那么，$\forall t({\phi }_1)$是公式。表示命题为“若对所有t使${\phi }_1$为真，则$\forall t({\phi }_1)$为真，否则$\forall t({\phi }_1)$为假”。

公式中运算符优先级(低到高）：算术比较运算符$\theta$、$\exists$和$\forall$、$\neg$、$\wedge$和$\vee$、$\Rightarrow$。加括号时，括号中的运算符优先。

关系代数转化为元组演算：

1. 并。 R ∪ S = { t ∣ R ( t ) ∨ S ( t ) } R\cup S=\{t|R(t) \vee S(t)\} R∪S={t∣R(t)∨S(t)}
2. 差。 R − S = { t ∣ R ( t ) ∧ ¬ S ( t ) } R - S=\{t|R(t) \wedge \lnot S(t)\} R−S={t∣R(t)∧¬S(t)}
3. 笛卡尔积。 R × S = { t ∣ ( ∃ u ) ( ∃ v ) ( R ( u ) ∧ S ( v ) ∧ t [ 1 ] = u [ 1 ] ∧ . . . ∧ t [ n ] = u [ n ] ∧ t [ n + 1 ] = v [ 1 ] ∧ . . . ∧ t [ n + m ] = v [ m ] ) } R \times S=\{t|(\exists u)(\exists v)(R(u)\wedge S(v)\wedge t[1]=u[1]\wedge ... \wedge t[n]=u[n]\wedge t[n+1]=v[1]\wedge ... \wedge t[n+m]=v[m])\} R×S={t∣(∃u)(∃v)(R(u)∧S(v)∧t[1]=u[1]∧...∧t[n]=u[n]∧t[n+1]=v[1]∧...∧t[n+m]=v[m])}
4. 投影。 π i 1 , i 2 , . . . , i k ( R ) = { t ∣ ( ∃ u ) ( R ( u ) ∧ t [ 1 ] = u [ i 1 ] ∧ t [ 2 ] = u [ i 2 ] ∧ . . . ∧ t [ k ] = u [ i k ] } \pi_{i_1,i_2,...,i_k}(R) =\{t|(\exists u)(R(u)\wedge t[1]=u[i_1]\wedge t[2]=u[i_2]\wedge ... \wedge t[k]=u[i_k]\} πi1​,i2​,...,ik​​(R)={t∣(∃u)(R(u)∧t[1]=u[i1​]∧t[2]=u[i2​]∧...∧t[k]=u[ik​]}
5. 选择。 σ F ( R ) = { t ∣ R ( t ) ∧ F } \sigma_F(R)=\{t|R(t) \wedge F\} σF​(R)={t∣R(t)∧F}

查询优化

查询处理是从数据库中提取数据的一系列活动。
查询处理的代价：总代价=I/O代价+CPU代价+内存代价（多用户环境）。
查询优化：为查询选择最有效的查询计划的过程。

优化的准则：

• 提早执行选取运算。
• 合并乘积与其后的选择运算为连接运算。
• 将投影运算与其后的其他运算同时进行，以避免重复扫描关系。
• 将投影运算和其前后的二木运算结合起来，使得没有必要为去掉某些字段再扫描一遍关系。
• 在执行连接前对关系做适当的预处理，就能快速地找到要连接的元组。方法有两种：索引连接法、排序合并连接法。
• 存储公共子表达式。