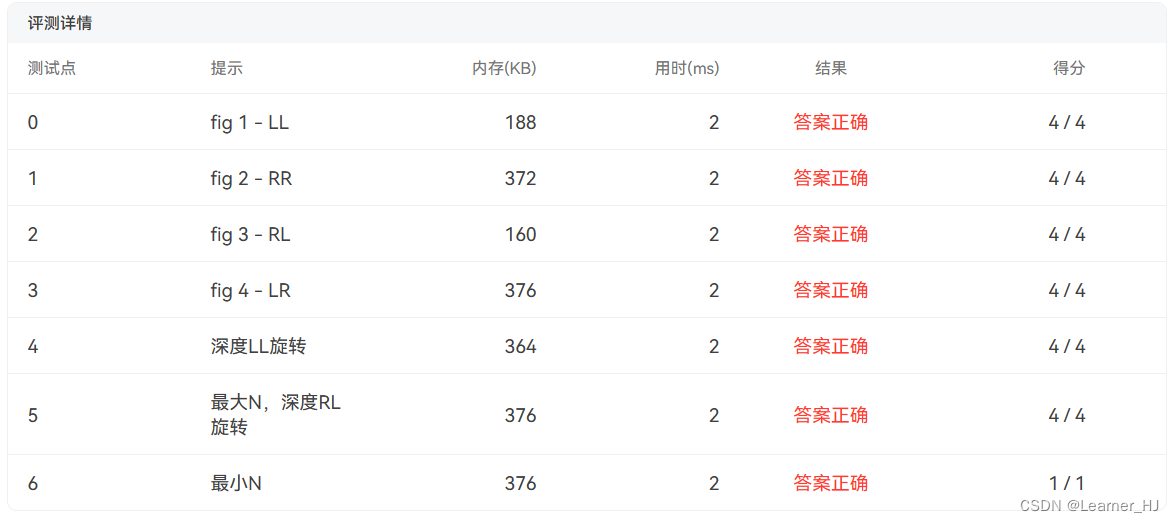
04-树5 Root of AVL Tree(浙大数据结构PTA习题）

news2024/11/19 15:35:40

04-树5 Root of AVL Tree 分数 25 作者陈越单位浙江大学

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

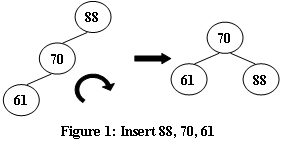
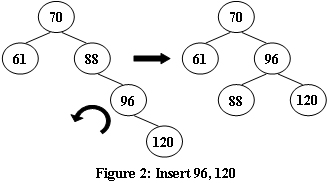
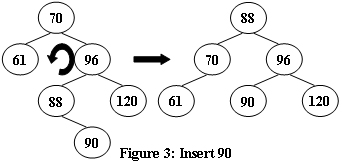
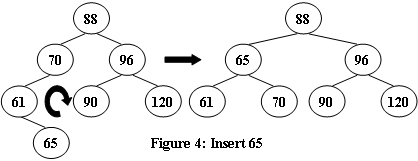
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

代码长度限制：16 KB 时间限制：400 ms 内存限制：64 MB

题目解析：

主要考察平衡二叉树的插入问题。若插入元素后不平衡，一共将有四种情况调整为平衡，即左单旋、右单旋、左-右双旋、右-左双旋，如下图所示。

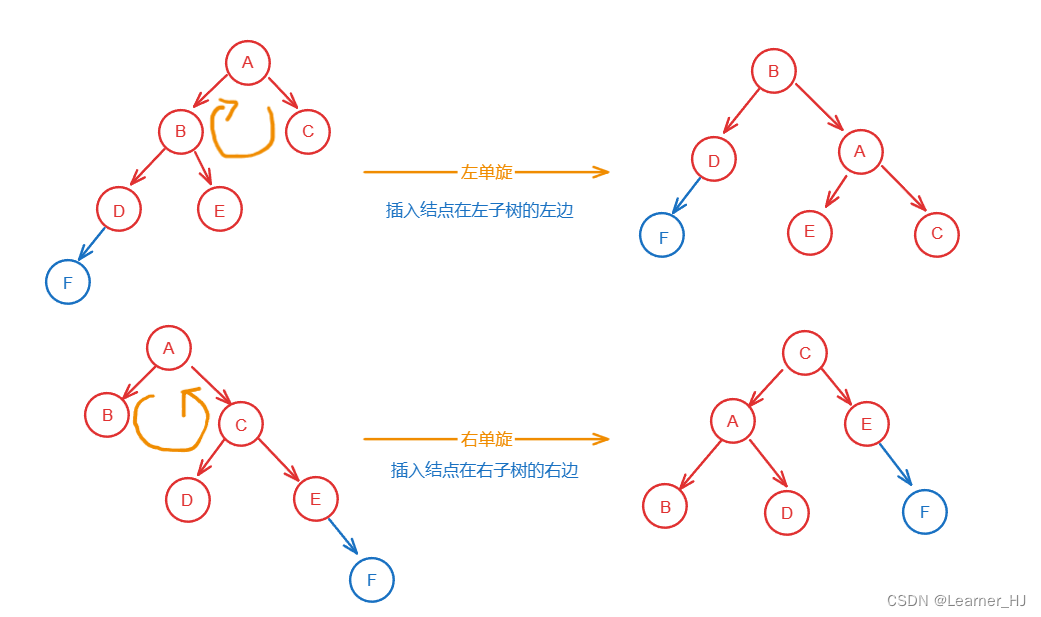
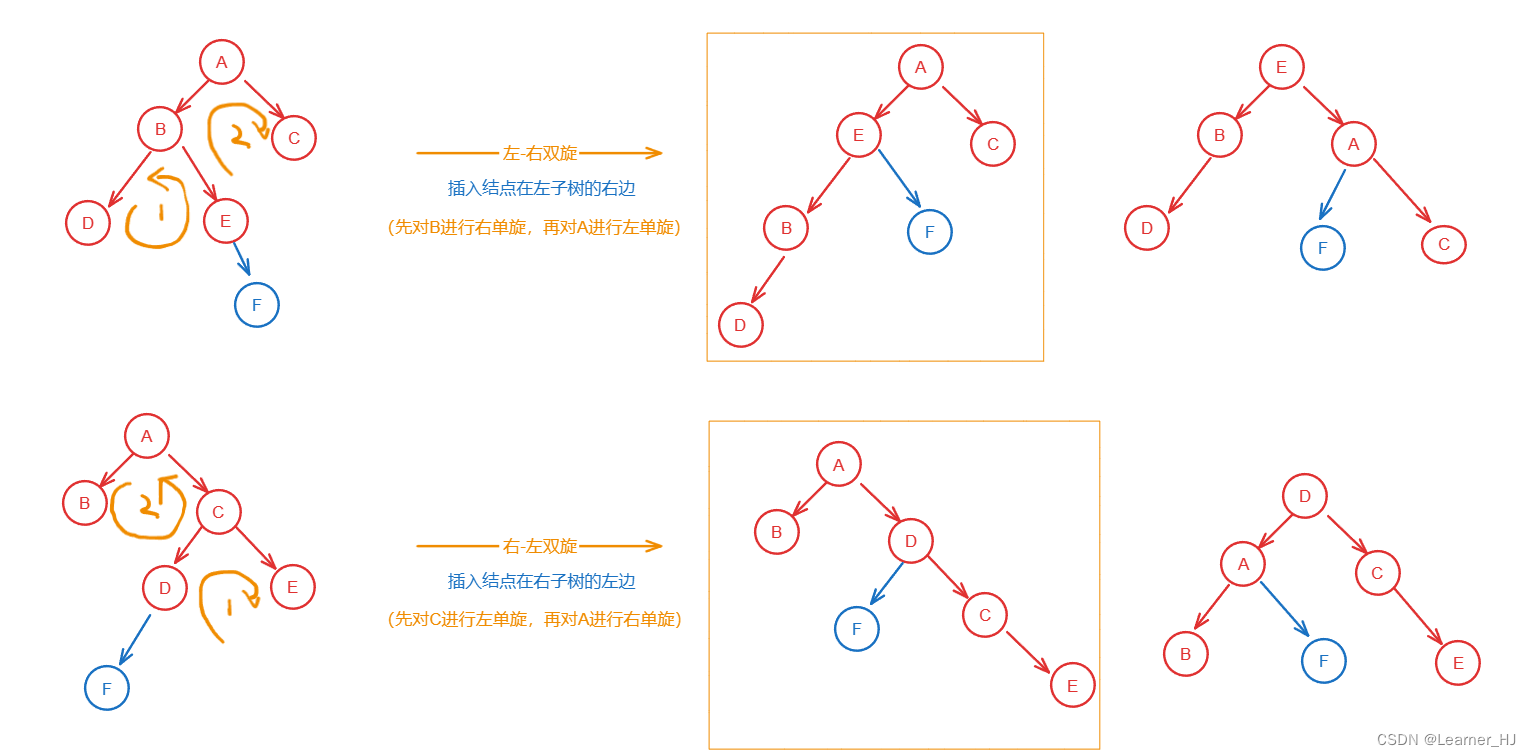
参考代码：

# include<stdio.h>
# include<stdlib.h>

typedef int ElementType;

typedef struct TreeNode* BinTree;
struct TreeNode{
	ElementType data;
	BinTree Left;
	BinTree Right;
};

BinTree SingleLeftRotation(BinTree Tree);
BinTree SingleRightRotation(BinTree Tree);
BinTree DoubleLRRotation(BinTree Tree);
BinTree DoubleRLRotation(BinTree Tree);
ElementType GetHeight(BinTree Tree);
ElementType Max(ElementType a, ElementType b);
BinTree InsertBinTree(BinTree Tree,ElementType X);

int main(){
	// 接收结点个数
	int N;
	scanf("%d",&N);
	// 创建一棵空平衡二叉树
	BinTree Tree = NULL;
	// 向平衡二叉树中插入结点
	int i,X;
	for(i=0;i<N;i++){
		scanf("%d",&X);
		Tree = InsertBinTree(Tree,X);
	}
	// 输出根结点数据
	printf("%d",Tree->data);
	return 0; 
}


// 向平衡二叉树中插入元素，并返回插入后的根结点 
BinTree InsertBinTree(BinTree Tree,ElementType X){
	// 如果是空树，则建树并返回
	if(Tree==NULL){
		Tree = (BinTree)malloc(sizeof(struct TreeNode));
		Tree->data = X;
		Tree->Left = Tree->Right = NULL;
		return Tree; 
	}
	// 递归插入 
	if(X<Tree->data){
		// 递归插入左子树
		Tree->Left = InsertBinTree(Tree->Left,X);
		// 判读是否平衡 
		if(GetHeight(Tree->Left)-GetHeight(Tree->Right)>1){
			if(X>Tree->Left->data){
				// 左-右双旋
				Tree = DoubleLRRotation(Tree); 
			}else{
				// 左单旋
				Tree = SingleLeftRotation(Tree); 
			}
		} 
	}else{
		// 递归插入右子树
		Tree->Right = InsertBinTree(Tree->Right,X);
		// 判读是否平衡 
		if(GetHeight(Tree->Right)-GetHeight(Tree->Left)>1){
			if(X<Tree->Right->data){
				// 右-左双旋
				Tree = DoubleRLRotation(Tree); 
			}else{
				// 右单旋
				Tree = SingleRightRotation(Tree); 
			}
		} 
	}
	return Tree;
}


// 左单旋，并返回旋转后的根结点 
BinTree SingleLeftRotation(BinTree Tree){
	// 进行旋转 
	BinTree Root = Tree->Left;
	Tree->Left = Root->Right;
	Root->Right = Tree;
	return Root;
}

// 右单旋，并返回旋转后的根结点
BinTree SingleRightRotation(BinTree Tree){
	// 进行旋转 
	BinTree Root = Tree->Right;
	Tree->Right = Root->Left;
	Root->Left = Tree;
	return Root; 
}

// 左-右双旋，并返回旋转后的根结点
BinTree DoubleLRRotation(BinTree Tree){
	// 先右旋再左旋 
	Tree->Left = SingleRightRotation(Tree->Left);
	BinTree Root = SingleLeftRotation(Tree);
	return Root;
} 

// 右-左双旋，并返回旋转后的根结点
BinTree DoubleRLRotation(BinTree Tree){
	// 先左旋再右旋
	Tree->Right = SingleLeftRotation(Tree->Right);
	BinTree Root = SingleRightRotation(Tree);
	return Root; 
	 
} 

// 递归获取树高
ElementType GetHeight(BinTree Tree){
	if(Tree==NULL)return 0;
	else return Max(GetHeight(Tree->Left),GetHeight(Tree->Right))+1;
} 

// 返回两者中的较大者 
ElementType Max(ElementType a, ElementType b){
	return a>b?a:b;
}