-
二分查找
二分查找高效的前提是数据结构是有序的
思路:1.排序
2.将数组折半,分成左右两个数组。
3.判断要查找的数和中间位置数值的大小,来判断要查找的数实在哪一半。
4.之后继续折半查找,直至找到这个数。图解:
首先是找出各个指针;

此时target>arr[mid],所以left=mid+1,然后更新arr[mid];

此时target<arr[mid],所以right=mid_1,然后更新arr[mid];

最后发现arr[mid]=target,结束function binarySearch(arr, target){ let start = 0; let end = arr.length - 1; if(!end){ return arr[0] === target ? 0 : -1; } if(end == 1){ return arr[0] === target ? 0 : arr[1] === target ? 1 : -1; } let middle; while(start <= end){ middle = start + ((end - start) >> 1) | 0; if(arr[middle] === target){ return middle }else if(target > arr[middle]){ start = middle + 1 }else{ end = middle - 1 } } return -1 } -
Master公式计算递归的时间复杂度
-
有些算法在处理一个较大规模的问题时,往往会把问题拆分成几个子问题,对其中的一个或多个问题递归地处理,并在分治之前或之后进行一些预处理、汇总处理。这时候我们可以得到关于这个算法复杂度的一个递推方程,求解此方程便能得到算法的复杂度。其中很常见的一种递推方程就是这样的:
设常数 a >= 1,b > 1,f(n) 为函数,T(n) 为非负整数,T(n) = a T(n / b) + f(n),则有:
- 若 f(n)=O(nlogba−ε),ε>0,那么 T(n)=Θ(nlogba)。
- 若 f(n)=Θ(nlogba),那么 T(n)=Θ(nlogbalogn)。
- 若 f(n)=Ω(nlogba+ε),ε>0,并且对于某个常数 c < 1 和充分大的 n 有 af(n/b)≤cf(n),那么 T(n)=Θ(f(n))。
比如常见的二分查找算法,时间复杂度的递推方程为 T(n) = T(n / 2) + θ(1),显然有 nlogba=n0=Θ(1),满足 Master 定理第二条,可以得到其时间复杂度为 T(n) = θ(log n)。
再看一个例子,T(n) = 9 T(n / 3) + n,可知 nlogba=n2,令ε取 1,显然满足 Master 定理第一条,可以得到 T(n) = θ(n ^ 2)。
来一个稍微复杂一点儿例子,T(n) = 3 T(n / 4) + n log n。nlogba=O(n0.793),取ε = 0.2,显然当 c = 3 / 4 时,对于充分大的 n 可以满足 a * f(n / b) = 3 * (n / 4) * log(n / 4) <= (3 / 4) * n * log n = c * f(n),符合 Master 定理第三条,因此求得 T(n) = θ(n log n)。
运用 Master 定理的时候,有一点一定要特别注意,就是第一条和第三条中的ε必须大于零。如果无法找到大于零的ε,就不能使用这两条规则。
参考: https://blog.gocalf.com/algorithm-complexity-and-master-theorem.html
-
斐波那契数列
问题描述:Fibonacci 数(Fibonacci Number)的定义是:F(n) = F(n - 1) + F(n - 2),并且 F(0) = 0,F(1) = 1。对于任意指定的整数 n(n ≥ 0),计算 F(n) 的精确值,并分析算法的时间、空间复杂度。// 斐波那契数列 递归 function fibonacci(n){ if (n==0) { return 0; } if (n==1) { return 1; } return fibonacci(n-1) + fibonacci(n-2); }一个看起来很直观、用起来很恐怖的算法就是递归法。根据 Fibonacci 的递推公式,对于输入的 n,直接递归地调用相同的函数分别求出 F(n - 1) 和 F(n - 2),二者相加就是结果。递归的终止点就是递推方程的初值,即 n 取 0 或 1 的时候。
这个算法的时间复杂度有着跟 Fibonacci 类似的递推方程:T(n) = T(n - 1) + T(n - 2) + O(1),很容易得到 T(n) = O(1.618 ^ n)(1.618 就是黄金分割,(1+5)/2)。空间复杂度取决于递归的深度,显然是 O(n)。
// 斐波那契数列 递推法 function fibonacci(n){ if (n == 0) { return 0; } if (n == 1) { return 1; } let a = [0, 1]; let n_i = 1; while(n_i < n) { n_i++; // 交换位置 let next = a[0] + a[1]; a[0] = a[1]; a[1] = next; } return a[1]; }虽然只是一字之差,但递推法的复杂度要小的多。这个方法就是按照递推方程,从 n = 0 和 n = 1 开始,逐个求出所有小于 n 的 Fibonacci 数,最后就可以算出 F(n)。由于每次计算值需要用到前两个 Fibonacci 数,更小的数就可以丢弃了,可以将空间复杂度降到最低。显然时间复杂度是 O(n),空间复杂度是 O(1)。
比较一下递归法和递推法,二者都用了分治的思想——把目标问题拆为若干个小问题,利用小问题的解得到目标问题的解。二者的区别实际上就是普通分治算法和动态规划的区别。
矩阵法:~
-
归并排序
// 归并排序 function process(arr, L, R) { if (L === R) { return; } let mid = L + ((R - L) >> 1); process(arr,L,mid); process(arr,mid+1,R); merge(arr,L,mid,R); } function merge(arr,L,mid,R) { let help = []; let i = 0; let p1 = L; let p2 = mid +1; while (p1 <= mid && p2 <=R) { help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++]; } while(p1 <= M) { help[i++] = arr[p1++] } while(p2 <= R) { help[i++] = arr[p2++] } for(let i = 0;i<help.length;i++) { arr[L + i] = help[i] } }
【算法基础(2)】二分查找和斐波那契数列
news2026/2/12 5:11:46
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/170098.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
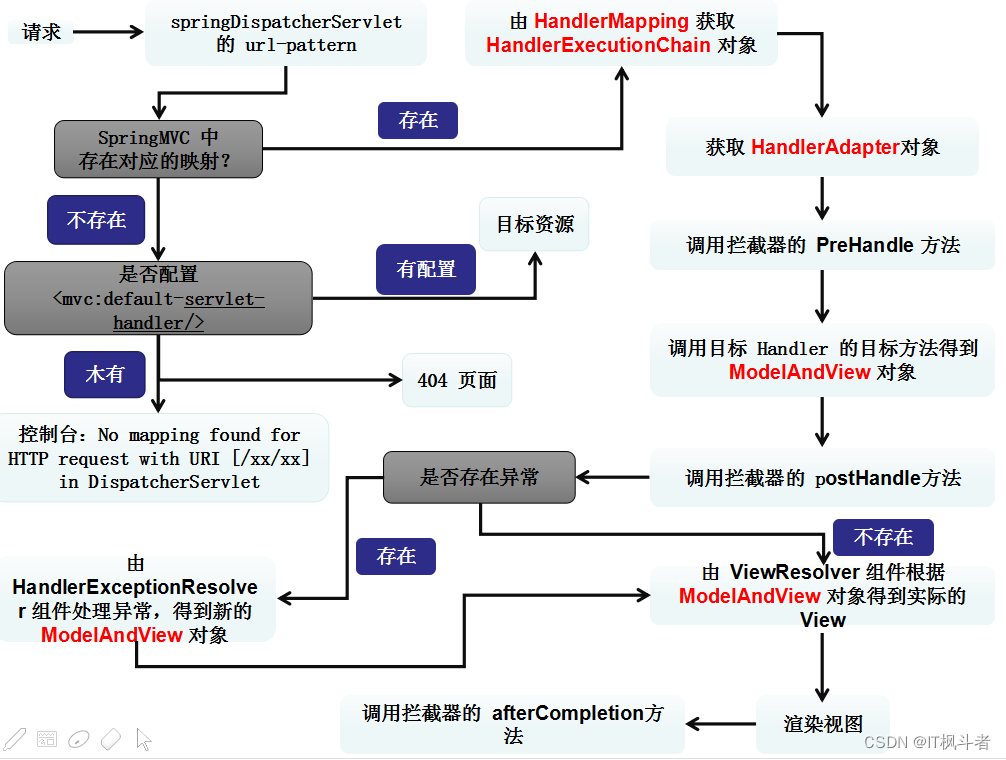
SpringMVC看这一篇文章就够了
第一章 SpringMVC的简介 Spring框架版本 4.3.29.RELEASE SpringMVC是什么 1
2
3
4
5
61. Spring家族的一个部分
2. 是JavaWeb三层架构中控制器层的解决方案
3. 是基于MVC思想的框架-- Model-- View-- ControllerSpringMVC知识点大纲SpringMVC功能简述 1
2
3
4
5
6
7
8
9
101. 作…
WEB前端有必要学会docker吗?0基础-45分钟带你学会(包含视频笔记案例源代码)
文章目录一、为什么要使用docker二、Windows10/11系统安装Docker Desktop三、如何判断电脑已经安装好docker四、docker前端应用实战:将vue项目打包为docker镜像运行1、将vue的项目进行构建,输出dist2、准备镜像内容3、制作镜像4、启动镜像五、如何发布镜…
【Leetcode】面试题 01.02. 判定是否互为字符重排、面试题 01.04. 回文排列
作者:一个喜欢猫咪的的程序员 专栏:《Leetcode》 喜欢的话:世间因为少年的挺身而出,而更加瑰丽。 ——《人民日报》 目录 面试题 01.02. 判定是否互为字符重排 面试题 01.04. 回文排列 面试题 …
水果店做微信活动推荐_分享水果店微信小程序制作步骤
试试做个小程序拯救你的店!让你做出有效果的活动,每笔钱都花在刀刃上!编辑第一,提升水果销量,降低损耗用水果店小程序做拼团、砍价、秒杀活动,并讲原本卖不完的水果,做成果盘吸引客人注册会员。…
点成分享|关于Grant水浴的一些FAQ
1、关于稳定性和均匀性
1)稳定性,是水浴中任何一点在达到恒温时不同时间下的温度规律性波动程度的描述,是通过浴槽中心点测定的,并表示为测量值的正负一半。系同点不同时的温度特性描述。
例如:SAP恒温水浴设定温度为…
unreal engine建模模式建模研究
Create PolyExt 挤出(需要闭合) image.pngPathExt 具有宽度挤出 (无需闭合) 如下图绘制一个形状后按鼠标左键确定绘制完成再移动鼠标控制厚度按鼠标左键确定后端后再移动鼠标确定高度 image.pngimage.pngPathRev Draw and revolve polypaths to create new objects 画和旋转pol…
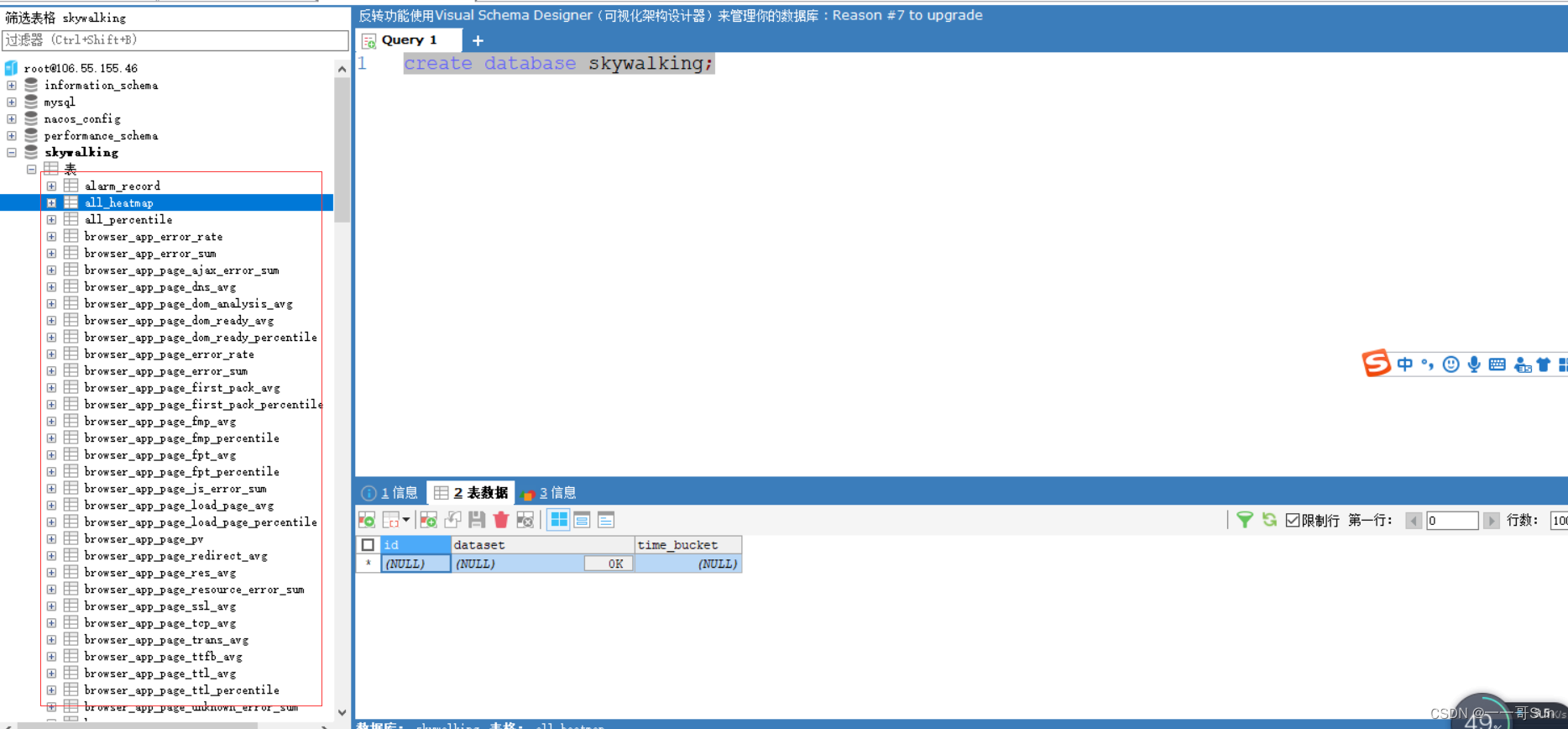
企业级监控项目Skywalking详细介绍,来看看呀
一. Skywalking概述一个优秀的项目,除了具有高拓展的架构、高性能的方案、高质量的代码之外,还应该在上线后具备多角度的监控功能。现在企业中的监控服务也有很多,Skywalking除了提供多维度、多粒度的监控之外,也提供了良好的图形…
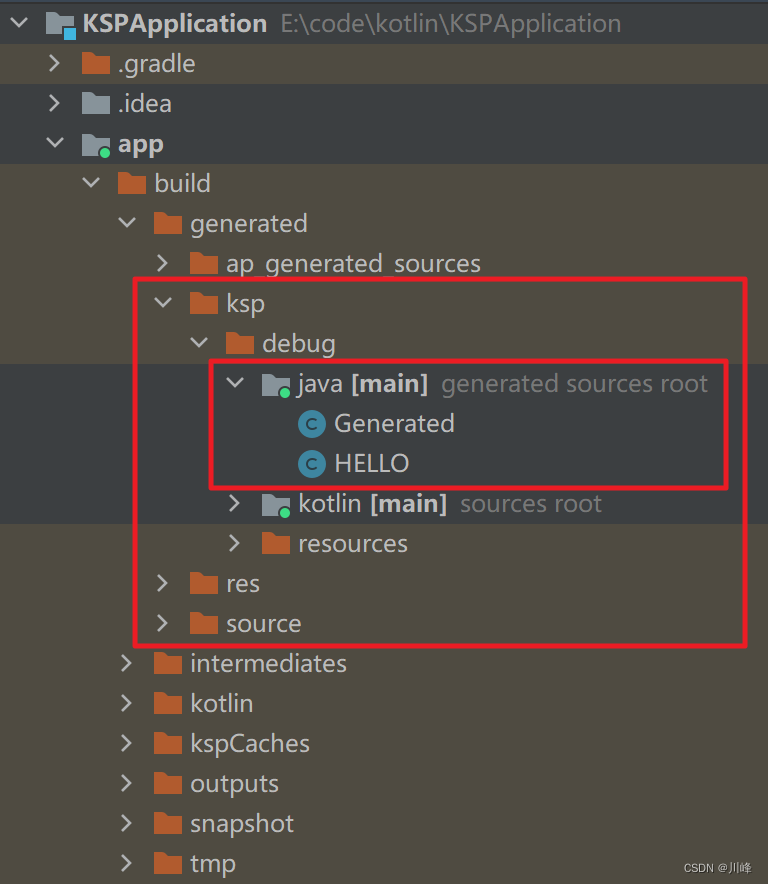
Kotlin 元编程之 KSP 全面突破
什么是元编程
没想到吧,这世上除了元宇宙,还有元编程,如果没有接触过,可能会有点懵,不过没关系,简单的说就是用代码来生成代码。实现元编程的传统常见手段主要是使用 APT注解处理器 JavaPoet 组合拳&…
JAVA基础知识巩固训练
目录
1. 案例一:逢 7 跳过
2. 案例二:数组元素求和
3. 案例三:判断两个数组是否相同⭐
4. 案例四:查找元素在数组中的索引
5. 案例五:数组元素反转
6. 案例六:评委打分
7. 案例七:随机产…
后端人眼中的Vue(五)
七、Vue生命周期 Vue的生命周期指的是Vue实例在页面中创建到销毁整个过程。Vue提供了在各个生命周期的钩子,钩子也叫Vue生命周期函数。这些生命周期函数是伴随着Vue实例创建、销毁的过程中自动触发的(不需要人为手动触发)。Vue实例生命周期…
产业互联网:补齐互联网的「短板」,重启互联网的「进化」
尽管在互联网时代出现了诸多的乱象,但是,我们依然无法否认互联网时代给人们的生产和生活带来的影响和改变。即使如此,我们依然无法否认互联网本身其实是存在着诸多的问题和弊病的,这些问题和弊病所导致的一个最为直接的结果&#…
【opencv】二维面找角点/关键点 实现
every blog every motto: You can do more than you think.
0. 前言
二维面找角点/关键点 实现
1. 正文
1.1 前提
1.1.1 显示函数
def show(arr):plt.imshow(arr)plt.show()def cvshow(arr):cv2.namedWindow(a, 0)cv2.imshow(a, arr)cv2.waitKey(0)cv2.destroyAllWindows…
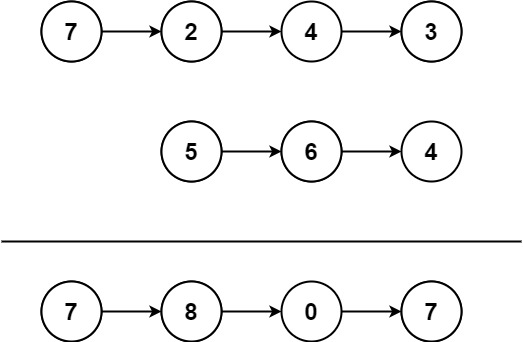
通关算法题之 ⌈链表⌋
链表
删除元素
203. 移除链表元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。
示例: 输入:head [1,2,6,3,4,5,6], val 6
输出:[1,2,3,4,5]c…
2022 IoTDB Summit:宝武智维徐少锋《Apache IoTDB 在宝武装备远程智能运维平台中的使用案例》...
12 月 3 日、4日,2022 Apache IoTDB 物联网生态大会在线上圆满落幕。大会上发布 Apache IoTDB 的分布式 1.0 版本,并分享 Apache IoTDB 实现的数据管理技术与物联网场景实践案例,深入探讨了 Apache IoTDB 与物联网企业如何共建活跃生态&#…
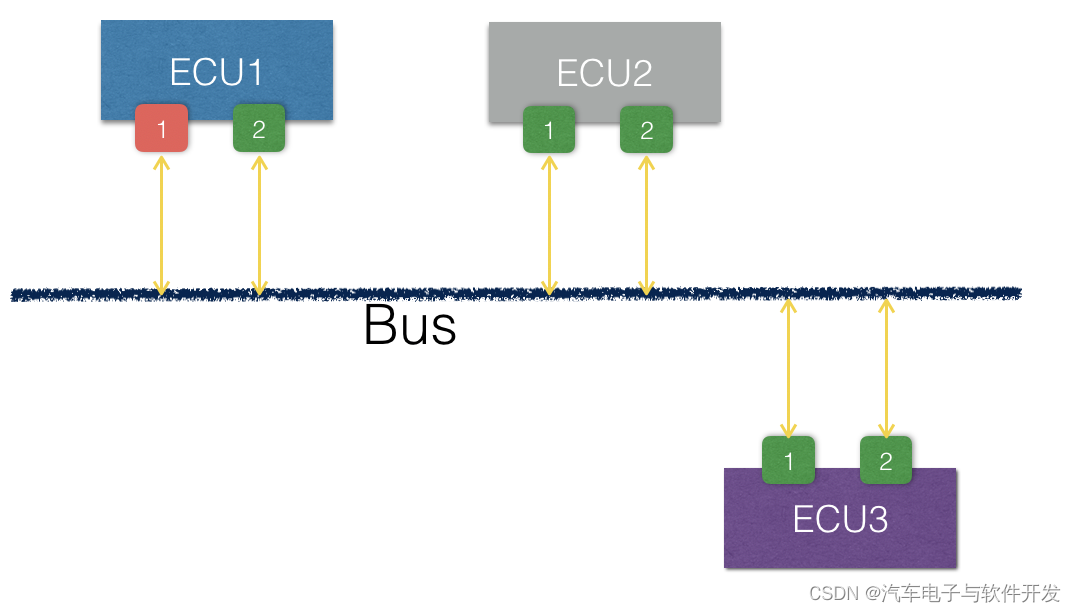
01【Vector CP】- 详解PN局部网络管理
Partial Networking概述
Partial Networking适用的ECU类型: 总线上依然有通信ECU关闭通信堆栈ECU要求降低功耗 Note:Partial Networking功能及其所有子功能是可选的,必须进行配置。为了控制此类ECU的关断和唤醒,CAN NM提供了一种额外的算法: NM PDU 消息中的用户数据部分…
企业数字化转型的关键一步,建立数据意识
数字化给社会带来的巨大的科技革命和产业革命,让数字经济成为新的高速增长的国民经济支柱,让数据变为第五大生产要素,发挥巨大价值,成为企业重要资产。不仅如此,在数字化的影响下,数字化转型成为了个人、机…
ue4.27空项目打包不卡ue5.1空项目打包运行卡的要命研究测试
知乎上有人提问 lumen是如何做到不卡顿的,我却不以为然,我的显卡虽然算不上好显卡,但是也不至于独立显卡一个空项目都玩不起吧,打个cf,玩腾讯模拟器和平精英吃鸡肯定还是会很流畅的. 一个空项目都卡,怎么能说是我电脑配置问题呢??? 再来看提示 image.pngimage.png反射设置的…
2023 过春年,烟花依然了无缘;这能难倒程序猿?一键三连过大年!
效果图镇楼 序
不知道是在什么时候,济南就开始都在传:“今年不再限制放烟花啦!”。一些集市上也开始有了售卖烟花的摊子 大家都很兴奋,很多小伙伴开始购买烟花。特别是今年特别火的 “加特林 😱” 但是大家兴奋劲还没…