一、数据结构的研究内容

1.1学生信息管理系统

1. 2人机对弈问题

1. 3最短路径问题

二、基本概念和术语

2.1数据，数据元素，数据项，数据对象

2.1.1 数据（Data）：

2.1.2 数据元素(Data Element)：

2.1.3 数据项(Data Item）：

2.1.4 数据对象（Data Object）：

2.2数据结构的定义和层次

2.2.1数据结构的定义

2.2.2数据结构的层次

2.3数据类型和抽象数据类型

2.3.1数据类型（Data Type）：

2.3.2抽象数据类型（Abstract Data Type，ADT) ：

三、算法和算法分析

3.1算法的定义及特性

3.2评价算法优劣的基本标准

一、数据结构的研究内容

数据结构主要研究非数值计算问题，即程序设计中操作的对象，以及这些对象之间的关系和操作；非数学问题无法用数学方程建立模型，如下三个实例

1.1学生信息管理系统

查找每个学生的基本信息，需要对这张信息表进行查询，如查找学号为2020010102同学的专业，每个学生的基本信息记录按顺序排列，形成了一种线性序列，呈现线性关系的数据结构。

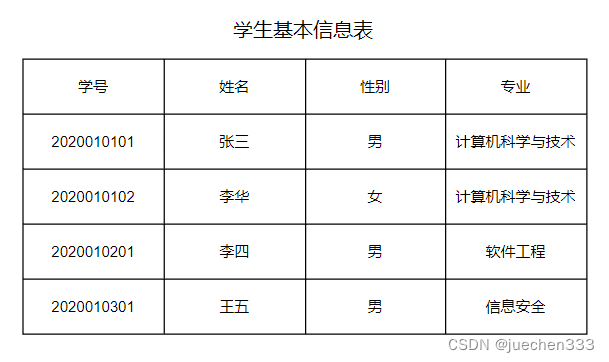
1. 2人机对弈问题

计算机之所以能和人对弈是因为已经将对弈的策略在计算机中存储好，把对弈过程中所有可能发生的情况及相应的对策都加以考虑。

以最简单的井字棋为例，初始状态是一个空的棋盘格局。对弈开始后，每下一步棋，则构成一个新的棋盘格局，且相对于上一个棋盘格局的可能选择可以有多种形式，因而整个对弈过程就如同“一棵倒长的树”。在这棵“树”中，从初始状态（根)到某一最终格局(叶子)的一条路径，就是一次具体的对弈过程。

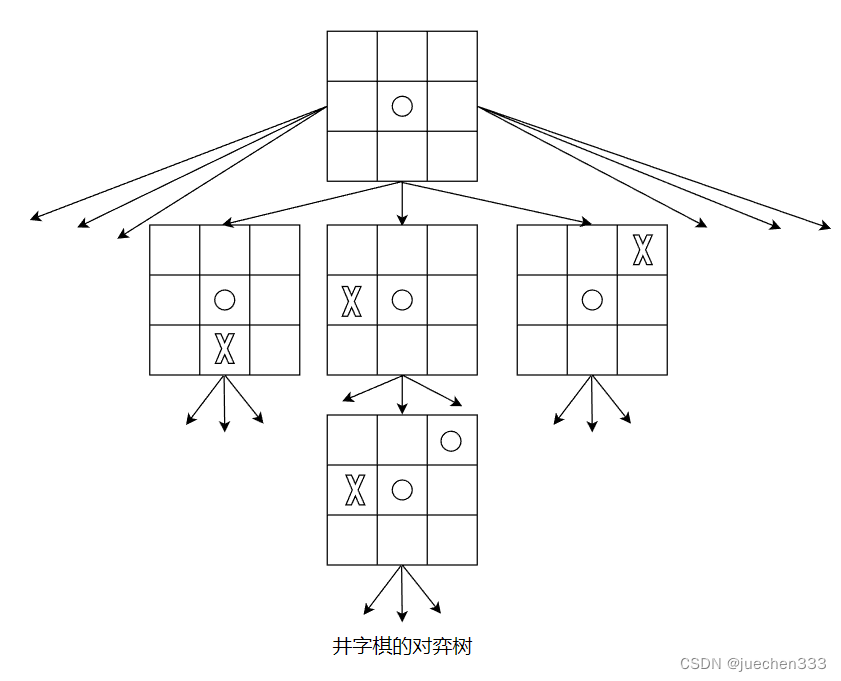
人机对弈问题的数学模型就是如何用树结构表示棋盘和棋子等，算法是博弈的规则和策略，这类数学模型称为“树”的数据结构。

1. 3最短路径问题

从城市A到城市D有多条线路，但每条线路的交通费不同，那么，如何选择一条线路，使得从城市A到城市D的交通费用最少呢？

可以把这类问题抽象为图的最短路径问题。如图所示，图中的顶点代表城市，有向边代表两个城市之间的通路，边上的权值代表两个城市之间的交通费。求解A到D的最少交通费用，就是要在有向图中A点（源点）到达D点(终点)的多条路径中，寻找一条各边权值之和最小的路径，即最短路径。

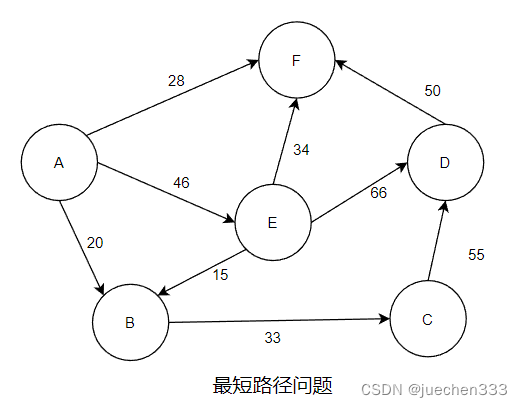
最短路径问题的数学模型是图结构，算法是求解两点之间的最短路径，这类数学模型称为“图”的数据结构。

二、基本概念和术语

2.1数据，数据元素，数据项，数据对象

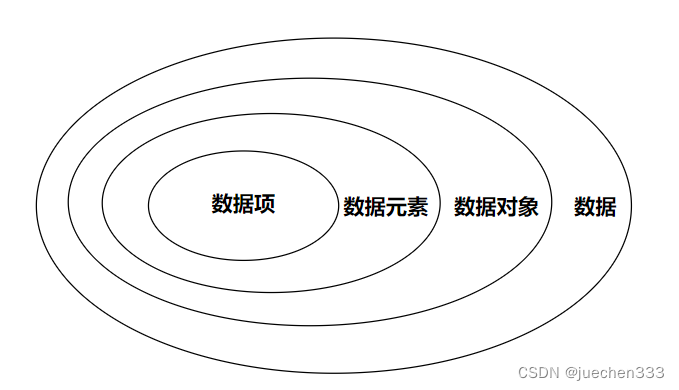
2.1.1 数据（Data）：

是客观事物的符号表示，是所有能输人到计算机中并被计算机程序处理的符号的总称。如数学计算中用到的整数和实数，文本编辑中用到的字符串，多媒体程序处理的图形、图像、声音及动画等通过特殊编码定义后的数据。

2.1.2 数据元素(Data Element)：

是数据的基本单位，在计算机中通常作为一个整体进行考虑和处理。在有些情况下，数据元素也称为元素、记录等。数据元素用于完整地描述一个对象，如前一节示例中的一名学生记录，树中棋盘的一个格局（状态)，以及图中的一个顶点等。

2.1.3 数据项(Data Item）：

是组成数据元素的、有独立含义的、不可分割的最小单位。例如，学生基本信息表中的学号、姓名、性别等都是数据项。

2.1.4 数据对象（Data Object）：

是性质相同的数据元素的集合，是数据的一个子集。例如：整数数据对象是集合N={0，±1，+2，…}，字母字符数据对象是集合C={'A'，'B'，…，Z' ,'a', 'b'，…，'z'}，学生基本信息表也可以是一个数据对象。由此可以看出，不论数据元素集合是无限集（如整数集)，或是有限集（如字母字符集)，还是由多个数据项组成的复合数据元素(如学生表)的集合，只要集合内的性质均相同，都可称之为一个数据对象。

2.2数据结构的定义和层次

2.2.1数据结构的定义

数据结构（Data Structure）：是相互之间存在一种或多种特定关系的数据元系的集合，换句话说，数据结构是带“结构”的数据元素的集合，“结构”就是指数据元素之间存在的关系。

2.2.2数据结构的层次

数据结构可分为逻辑结构和存储结构，同一逻辑结构采用不同的存储方法，可以得到不同的存储结构。

①逻辑结构

从逻辑关系上描述数据，它与数据的存储无关，是独立于计算机的。因此，数据的逻辑结构可以看作是从具体问题抽象出来的数学模型。
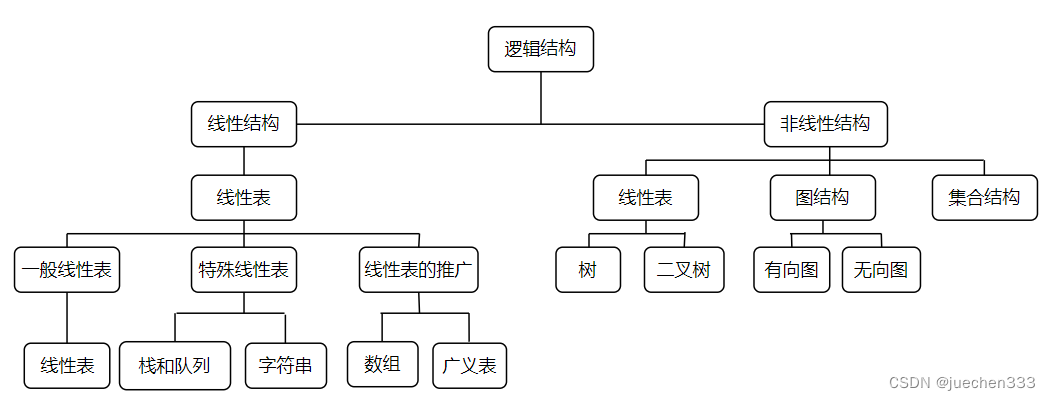
数据的逻辑结构有两个要素：一是数据元素（数据的基本单位）；二是关系，关系是指数据元素间的逻辑关系。根据数据元素之间关系的不同特性，通常有四类基本结构：线性结构，树结构，图结构，集合结构，其中集合结构、树结构和图结构都属于非线性结构。

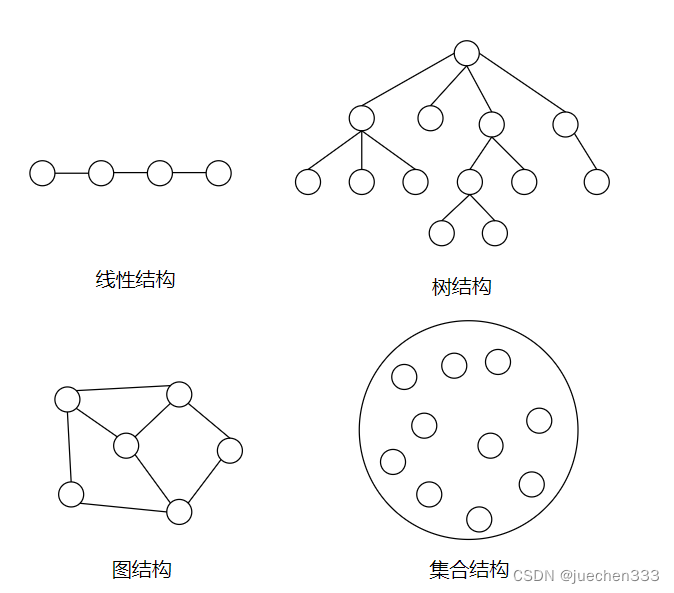
线性结构包括线性表、栈和队列（具有特殊限制的线性表，数据操作只能在表的一端或两端进行)、字符串（也是特殊的线性表，其特殊性表现在它的数据元素仅由一个字符组成)、数组（是线性表的推广，它的数据元素是一个线性表)、广义表（也是线性表的推广，它的数据元素是一个线性表，但不同构，即或者是单元素，或者是线性表)。非线性结构包括树（具有多个分支的层次结构）和二叉树（具有两个分支的层次结构）、有向图（一种图结构，边是顶点的有序对）和无向图（另一种图结构，边是顶点的无序对）。如图所示：

②存储结构

数据对象在计算机中的存储表示称为数据的在储结构，也称为物理结构。把数据对象存储到计算时，通常要求既要存储各数据元素的数据，又要存储数据元素之间的逻辑关系，数据元素在计算机内用一个结点来表示。数据元素在计算机中有两种基本的存储结构，分别是顺序存储结构和链式存储结构。

（1）顺序存储结构

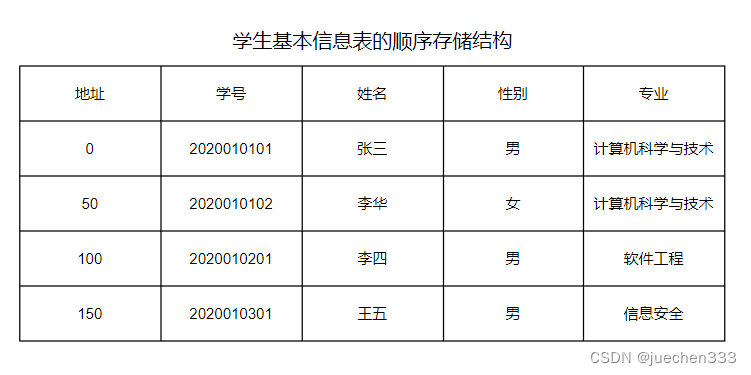
顺序存储结构是借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系，通常借助程序设计语言的数组类型来描述。
对于前面的“学生基本信息表”，假定每个结点（学生记录）占用50个存储单元，数据从0号单元开始由低地址向高地址方向存储，对应的顺序存储结构如图所示：

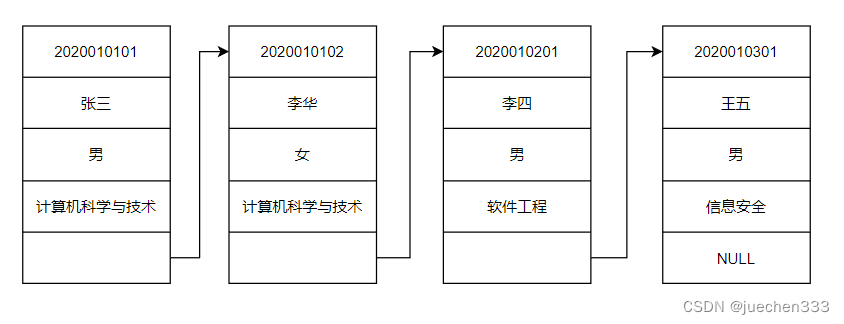
（2）链式存储结构

为了表示结点之间的关系，需要给每个结点附加指针字段，用于存放后继元素的存储地址。所以链式存储结构通常借助于程序设计语言的指针类型来描述。

2.3数据类型和抽象数据类型

2.3.1数据类型（Data Type）：

是一个值的集合和定义在这个值集上的一组操作的总称。数据类型是高级程序设计语言中的一个基本概念，前面提到过顺序有储结构可以借助程序设计语言的数组类型描述，链式存储结构可以借助指针类型描述，所以数据类型和数据结构的概念密切相关。

在程序设计语言中，每一个数据都属于某种数据类型。类型明显或隐含地规定了数据的取值范围、存储方式以及允许进行的运算。例如，C语言中的整型变量，其值集为某个区间上的整数（区间大小依赖于不同的机器），定义在其上的操作为加、减、乘、除和取模等算术运算；而实型变量也有自己的取值范围和相应运算，比如取模运算是不能用于实型变量的。程序设计语言允许用户直接使用的数据类型由具体语言决定，数据类型反映了程序设计语言的数据描术和处理能力。C语言除了提供整型、实型、字符型等基本类型数据外，还允许用户自定义各种类型数据。例如数组、结构体和指针等。

2.3.2抽象数据类型（Abstract Data Type，ADT) ：

一般指由用户定义的，表示应用问题的数学模型，以及定义在这个模型上的一组操作的总称，具体包括三部分：数据对象，数据对象上关系的集合，对数据对象的基本操作的集合。

抽象就是抽取出实际问题的本质。在计算机中使用二进制数来表示数据，在汇编语言中则可给出各种数据的十进制表示，它们是二进制数据的抽象，使用者在编程时可以直接使用，不必考虑实现细节。在高级语言中，则给出更高一级的数据抽象，出现了数据类型，如实型、字符型等，可以进一步利用这些类型构造出线性表、栈、队列、树、图等复杂的抽象数据类型。