1. 关注一个序列

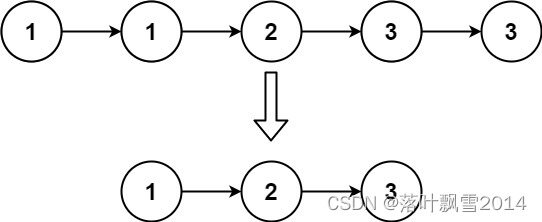
做RNN的时候，处理不了太长的序列，因为把整个序列信息全部放在隐藏状态中，所有东西都放进去，当时间步很长的话，隐藏状态就会累积太多东西，就可能对很前面的信息不那么容易抽取出来了。

所以观察序列的话，不是每个观察值都是同等重要的。就如一篇文章中，也有一些关键句。

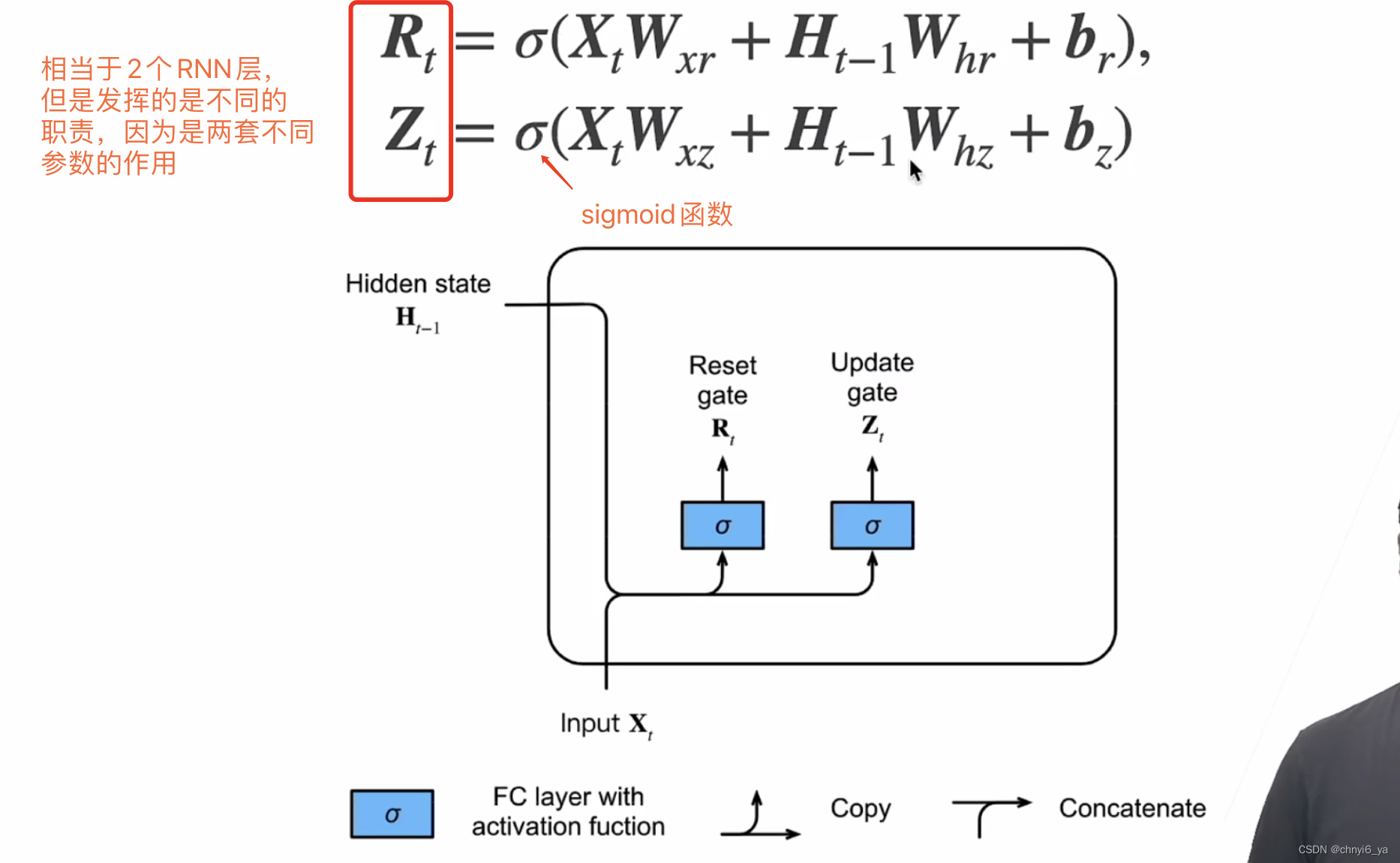
在这里插入图片描述

2. 门

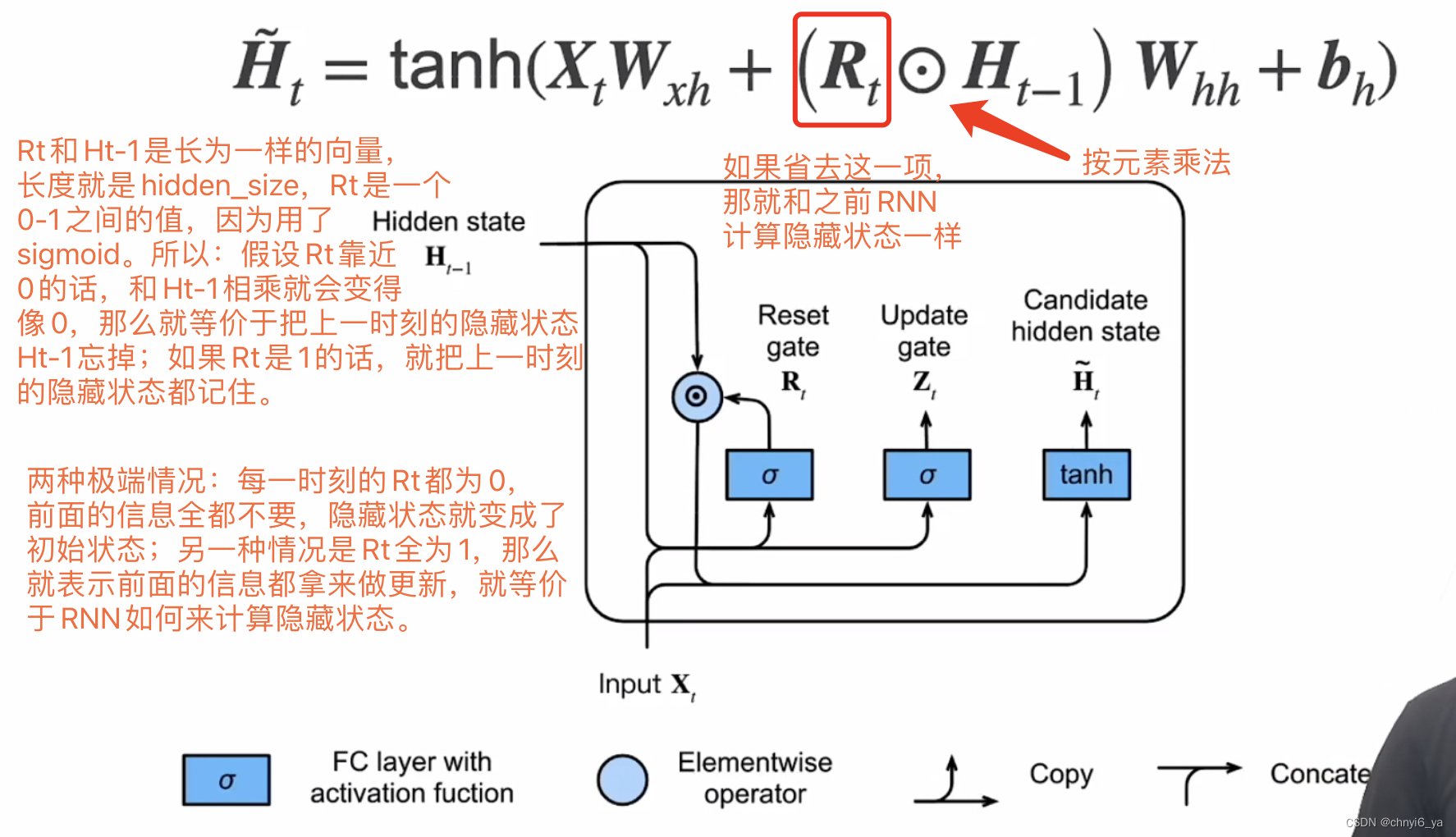
在这里插入图片描述

3. 候选隐状态

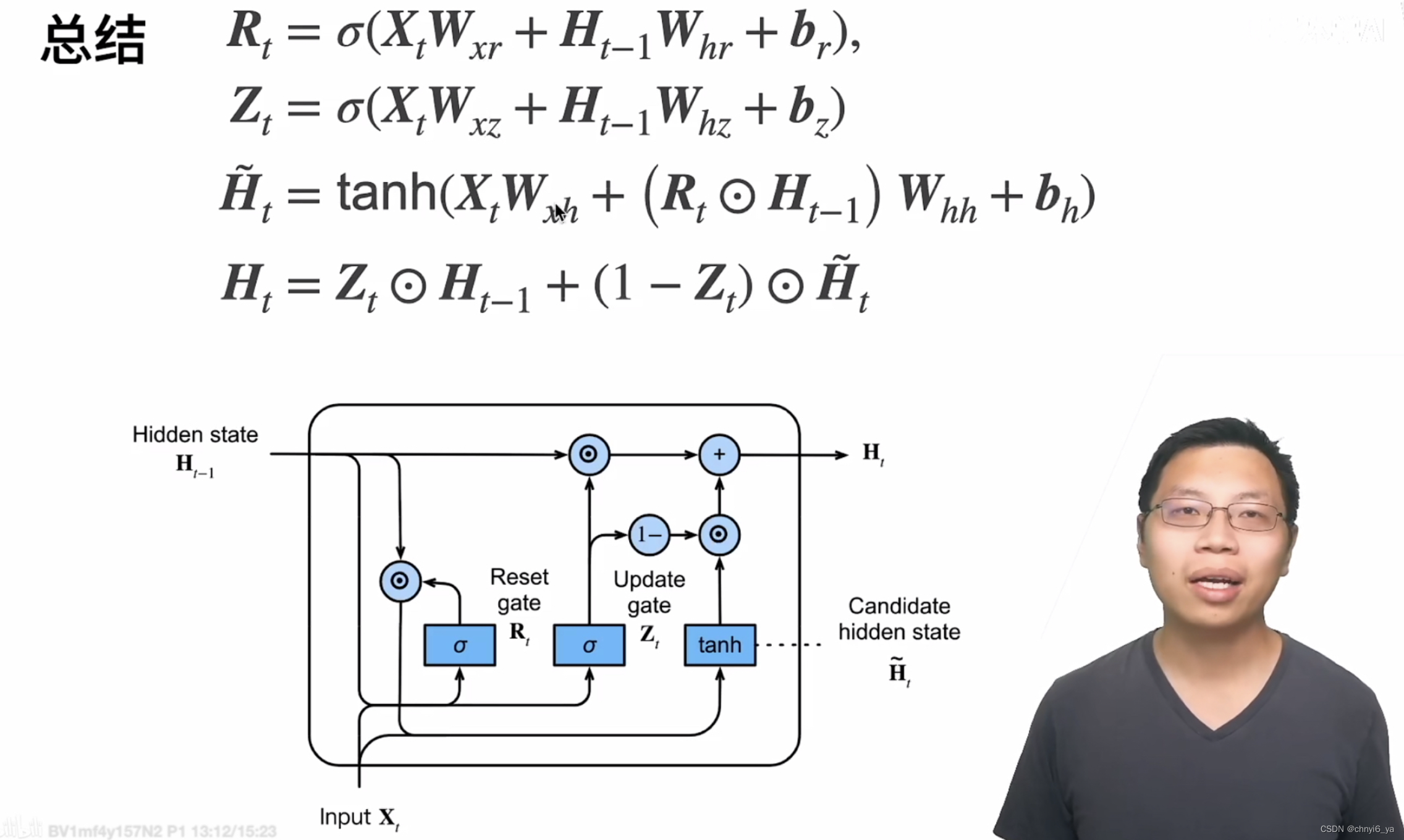
在这里插入图片描述

4. 真正的隐状态

在这里插入图片描述

5. 总结

gru引入了两个额外的门，Wxr、Wxz、Wxh都是可学习的参数，这样就是以前RNN可学习参数的3倍，2个极端情况：Zt=1，那么这一时刻的隐藏状态就等于上一个隐藏状态，且忽略掉当前时刻的Xt；Zt=0，Rt=0时，这一时刻的隐藏状态就只需要关注当前时刻的输入Xt。

所以通过两个门Rt和Zt来控制在这两种极端情况之间做一些可学习参数的调整，使得可以控制：是多看现在的输入Xt呢，还是多看过去的信息。

其中，一种特殊情况是Zt=0，Rt=1时，就会回到RNN的情况，通过当前时刻的Xt和上一时刻的隐藏状态来更新。

在这里插入图片描述

6. 代码实现

6.1 从零开始实现

首先，我们读取时间机器数据集：

import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

1. 初始化参数模型

下一步是初始化模型参数。我们从标准差为 0.01 的高斯分布中提取权重，并将偏置项设为 0 ，超参数num_hiddens定义隐藏单元的数量，实例化与更新门、重置门、候选隐状态和输出层相关的所有权重和偏置。

# 初始化模型参数
def get_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    # 均值为0，方差为0.01的随机初始化权重
    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01

    # 辅助函数，包括：输入到hidden的W，hidden到hidden的W以及偏置
    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))

    # 创建了9个可以学习的参数
    W_xz, W_hz, b_z = three()  # 更新门参数
    W_xr, W_hr, b_r = three()  # 重置门参数
    # 相比RNN，GRU多出了上面这两行
    W_xh, W_hh, b_h = three()  # 候选隐状态参数

    # 输出层参数，也是可学习的参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)

    # 附加梯度，总共11个可以学习的参数
    params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

2. 定义模型

现在我们将定义隐状态的初始化函数init_gru_state。与 rnn_scratch中定义的init_rnn_state函数一样，此函数返回一个形状为（批量大小，隐藏单元个数）的张量，张量的值全部为零。

def init_gru_state(batch_size, num_hiddens, device):
	# 返回一个tuple，是全0的形状为（批量大小，隐藏单元个数）的张量
    return (torch.zeros((batch_size, num_hiddens), device=device), )

现在我们准备定义门控循环单元模型，模型的架构与基本的循环神经网络单元是相同的，只是权重更新公式更为复杂。

def gru(inputs, state, params):
    W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    # outputs是每个时刻的输出
    outputs = []
    for X in inputs: # inputs的形状是（num_steps,batch_size,vocab_size)
        # @ 这个符号表示矩阵乘法，相当于torch.matmul()
        # 等号右边的H是前一个时刻的H，左边的H是当前时刻的H
        Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
        R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
        H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
        H = Z * H + (1 - Z) * H_tilda
        Y = H @ W_hq + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

3. 训练与预测

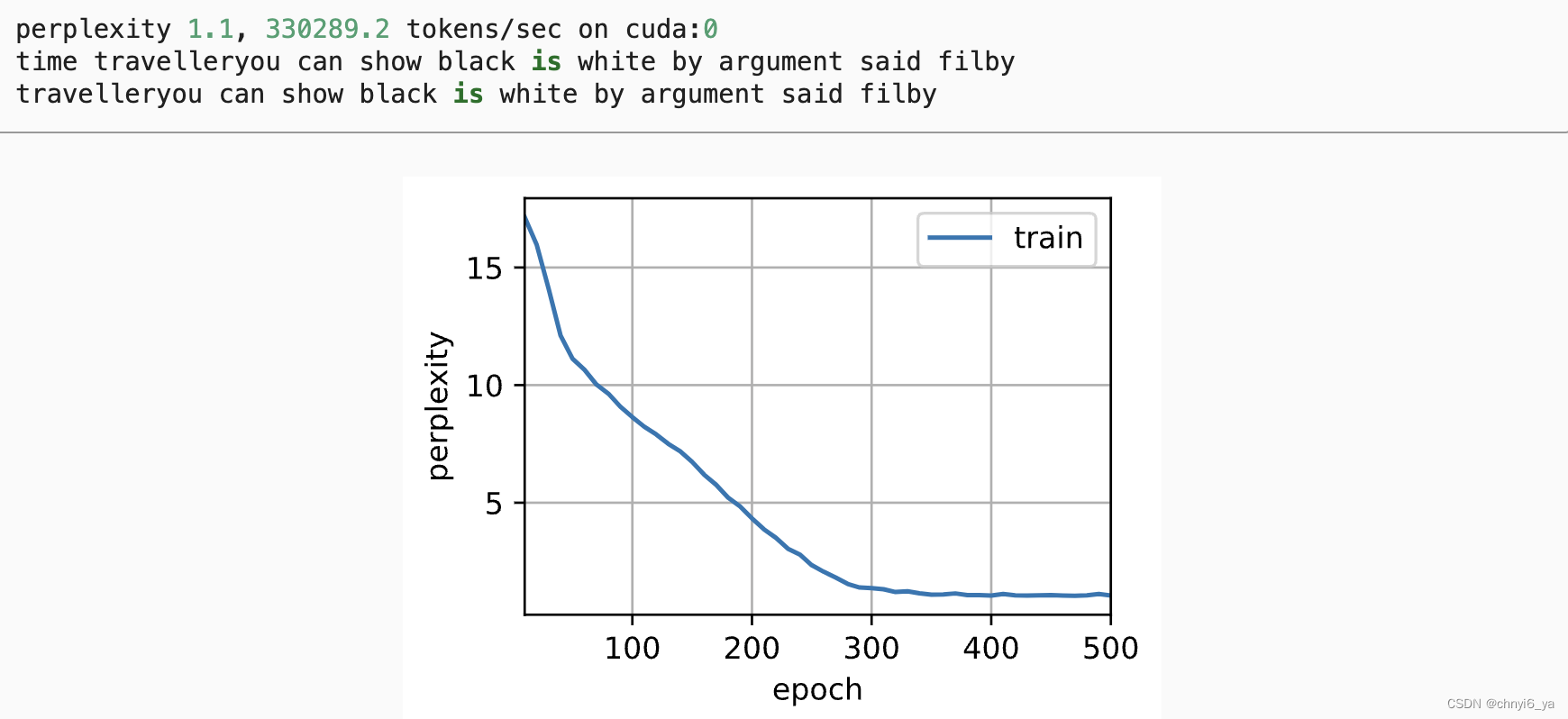
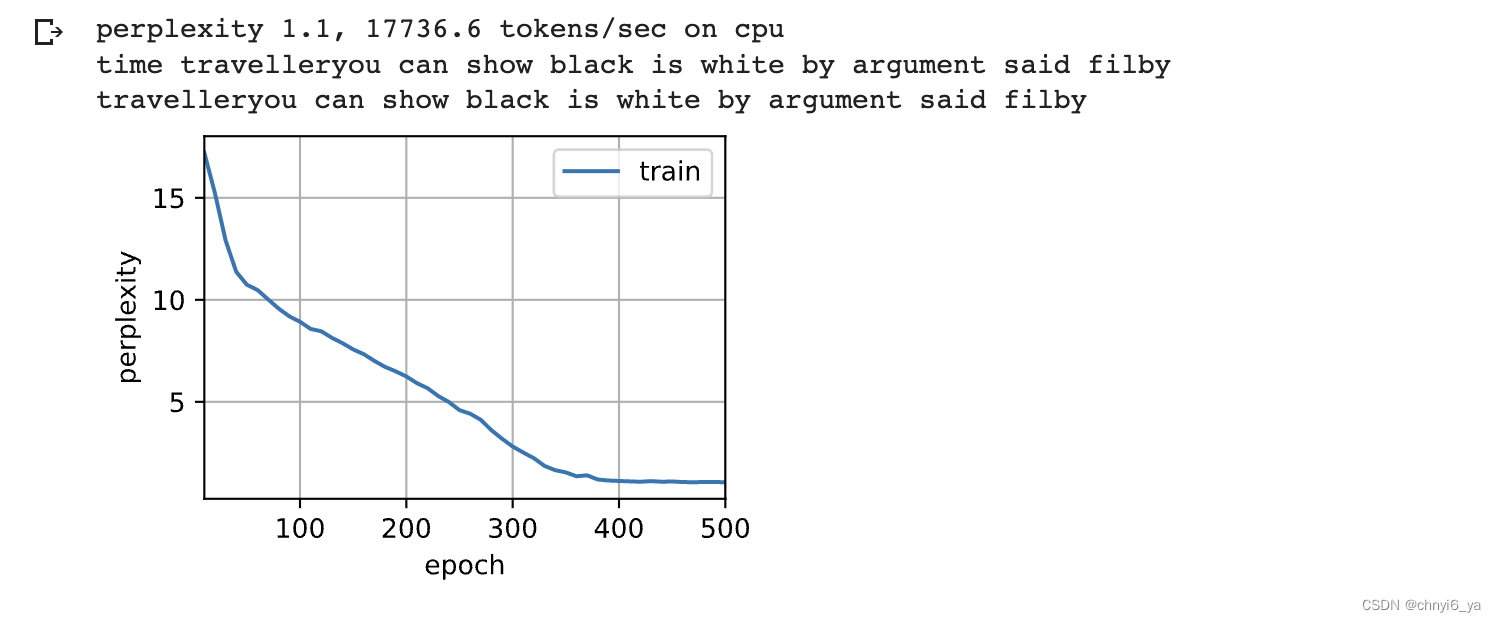
训练和预测的工作方式与rnn_scratch完全相同。训练结束后，我们分别打印输出训练集的困惑度，以及前缀“time traveler”和“traveler”的预测序列上的困惑度。

vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
# 之前实现的RNNModelScratch足够通用
# 传入"初始化模型参数"get_params，以及"初始化状态函数"init_gru_state，
# 以及"forward"如何计算，也就是用的网络结构gru，就能得到GRU模型
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,
                            init_gru_state, gru)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

运行结果：

在这里插入图片描述

6. 2 简介实现

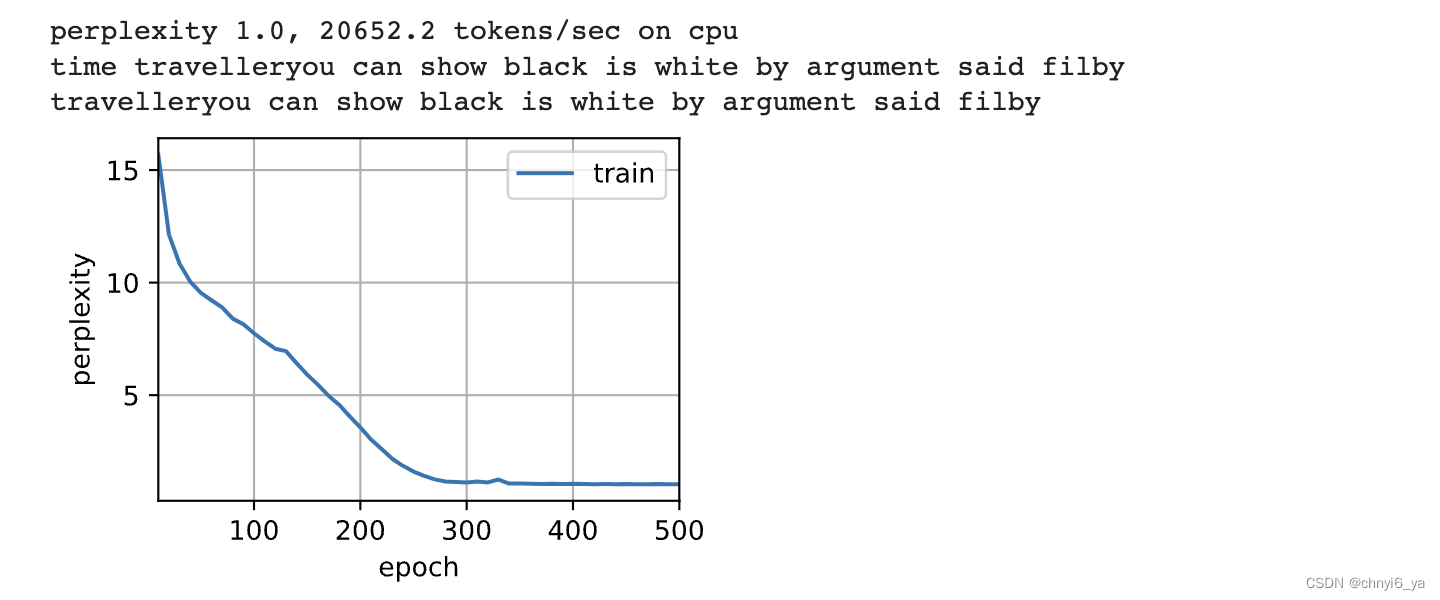
高级API包含了前文介绍的所有配置细节，所以我们可以直接实例化门控循环单元模型。这段代码的运行速度要快得多，因为它使用的是编译好的运算符而不是Python来处理之前阐述的许多细节。

num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)