2023.1.17
Affine层:
在神经网络的正向传播中,为了计算加权信号的总和,使用矩阵乘积运算。
比如:
import numpy as np
x = np.arange(6).reshape(2, 3) # (2,3)
w = np.arange(6).reshape(3, 2) # (3,2)
b = np.arange(4).reshape(2, 2) # (2,2)
y = np.dot(x, w) + b # 要符合线性代数运算规则
print(y)
# [[10 14]
# [30 43]]然后y传递到激活函数层转换后在传递给下一层神经网络。
在深度学习中,把正向传播中进行的矩阵乘积运算称为“仿射变换”。称仿射变换的处理实现称为Affine层。
仿射变换:一次线性变换(加权乘积)和一次平移(偏置)
Affine层的计算图:观察正向传播和反向传播,反向传播时,我们要结合线性代数考虑矩阵的形状,求出“dot 节点”的推导式子。
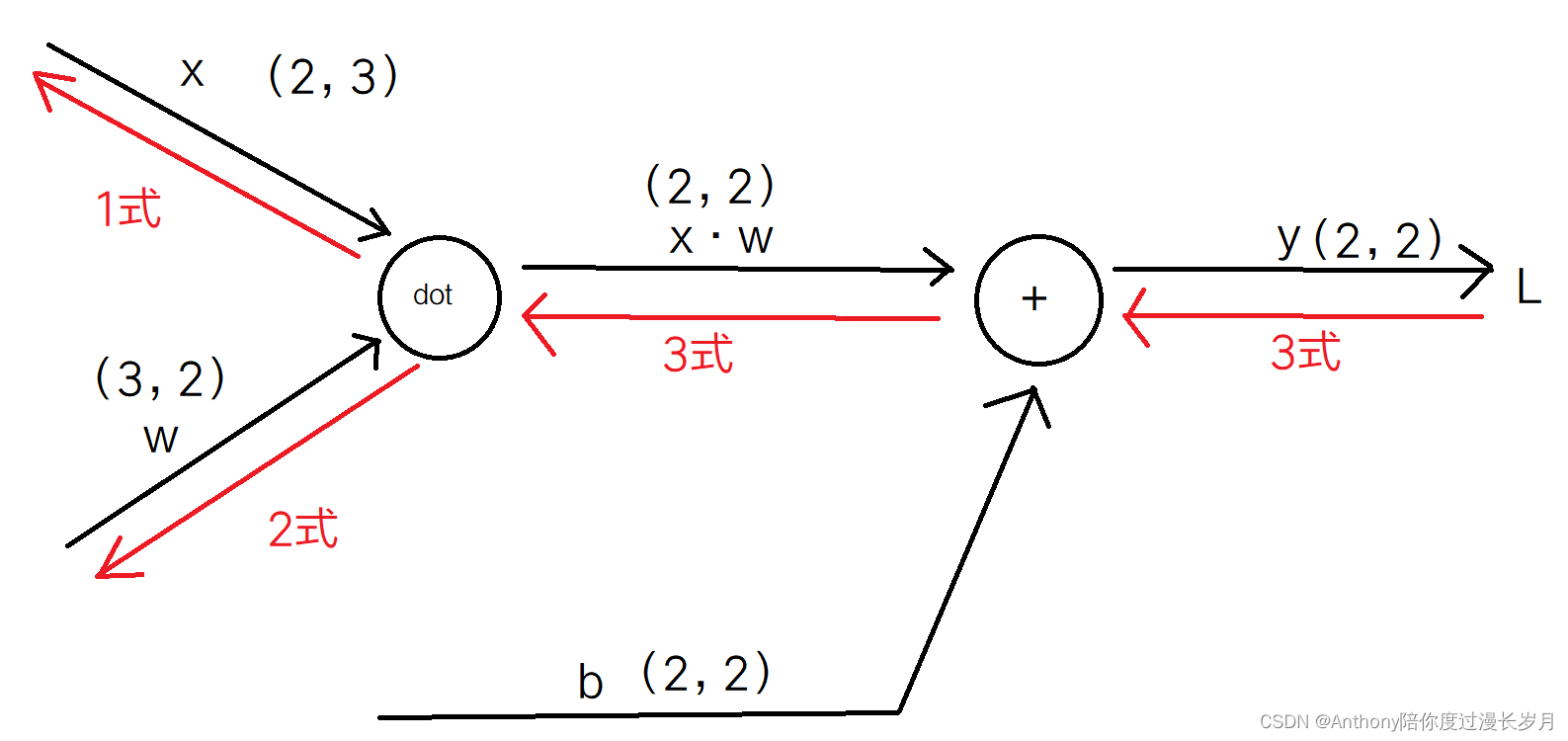
1式: ;
2式: ;
3式: ;
关于加法节点的传播在这篇文章:https://blog.csdn.net/m0_72675651/article/details/128695488
代码实现:
import numpy as np
class Affine:
def __init__(self, w, b):
self.w = w
self.b = b
self.x = None
self.dw = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.w) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.w.T)
self.dw = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dx
x = np.arange(6).reshape(2, 3)
w = np.arange(6).reshape(3, 2)
b = np.arange(4).reshape(2, 2)
a = Affine(w, b)
y = a.forward(x)
y1 = a.backward(y)
print(y, '\n', y1)输出结果:
[[10 14]
[30 43]]
[[ 14 62 110]
[ 43 189 335]]
Softmax层:
我们都知道soft函数会将输入的值正规化后再输出。回忆一下Softmax函数:
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x)
return np.exp(x) / np.sum(np.exp(x))
通过MNIST数据来演示:
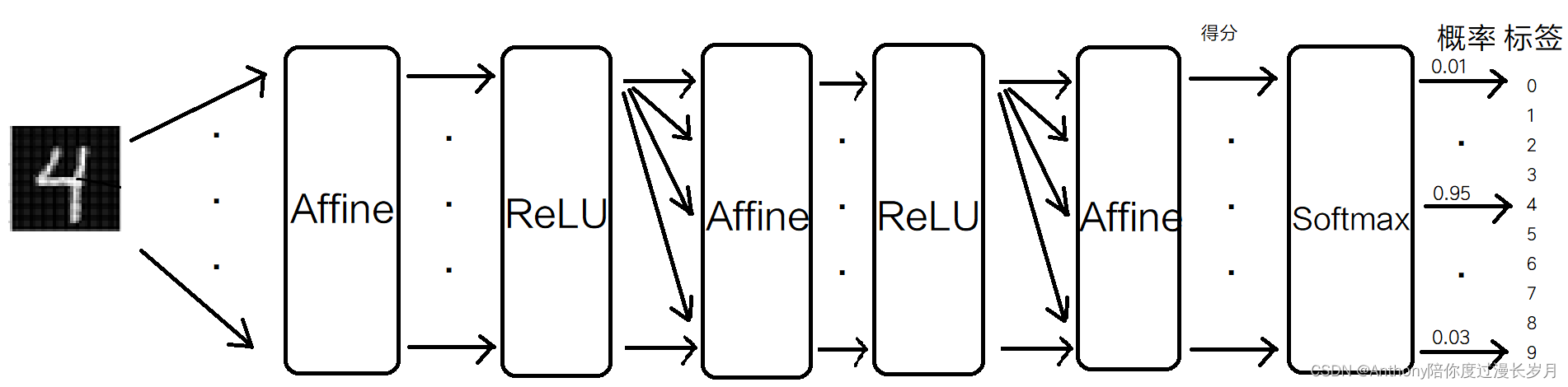
输入图像经过Affine层和ReLU层进行转换,因为MNIST数据有10类,输出层设计为Softmax层有10个输出,上层输入经过这里会有正规化过程。
在神经网络中,进行的处理有推理和学习两个阶段,其中推理阶段通常不需要softmax层,比如在上图中MNIST识别中以最后一个Affine层作为结果,其没有正规化,将这样的结果称为“得分”,也就是说,当神经网络的推理只需要一个答案(一个正确解标签)的情况下,我们只对“得分”的最大值感兴趣,所以不需要softmax层;
当我们在学习阶段时,我们需要softmax层,因为我们需要计算损失函数优化神经网络模型,我们就需要监督数据标签t和输出正确解标签y参与计算损失函数(y需要正规化) ;
Softmax-with-loss层:
接下来实现Softmax层 ,但是这包含到损失函数,所以结合交叉熵误差函数,称为Softmax-with-loss层;交叉熵误差: 。
(交叉熵误差函数参考这篇文章:https://blog.csdn.net/m0_72675651/article/details/128592167)
我们先用计算图先观察:
为了简化而细致的展现,我们假设最后一层Affine层只传递给softmax层3个得分;
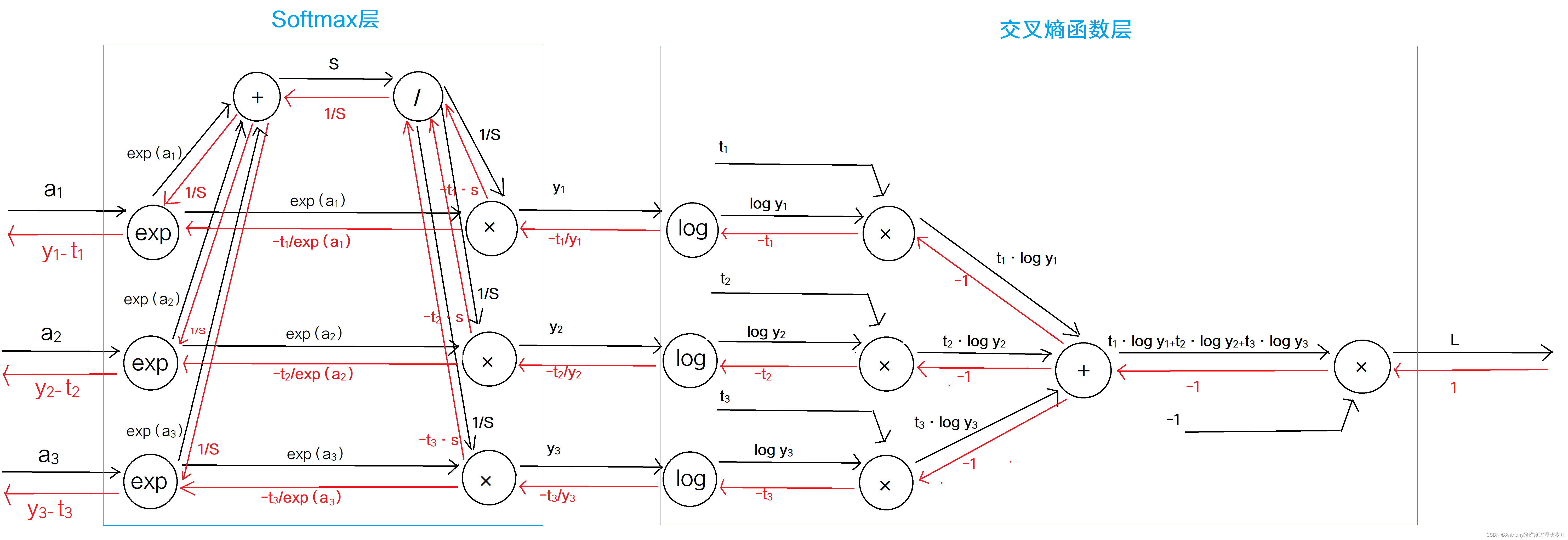
“exp 节点”:在正向传播时表示y=exp(x),由指数函数的数学解析式可得 ;
我们可以观察到最后传播得到了 的结果,是softmax层输出结果与监督数据的差分。因此,这里有一个重要的性质,神经网络会把这样的差分传递给前面的层。
假如这里有一个监督标签(0,1,0),而softmax层的输出结果是(0.1,0.1,0.8),显然这是没有正确分类,而他的差分是(0.1,-0.9,0.8),这个大差分会向前面传播的层传播,所以前面的层也会学习到这个“大”内容;假如这里有一个监督标签(0,1,0),而softmax层的输出结果是(0.005,0.99,0.05),显然这是正确分类,而他的差分是(0.005,-0.01,0.05),这个小差分会向前面传播的层传播,所以前面的层也会学习到这个“小”内容;
import numpy as np
def cross_entropy_error(y, t):
delta = 1e-7
return -1 * np.sum(t * np.log(y + delta))
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x)
return np.exp(x) / np.sum(np.exp(x))
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(y, t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx