第六章 傅里叶分析 处理图像频率信息
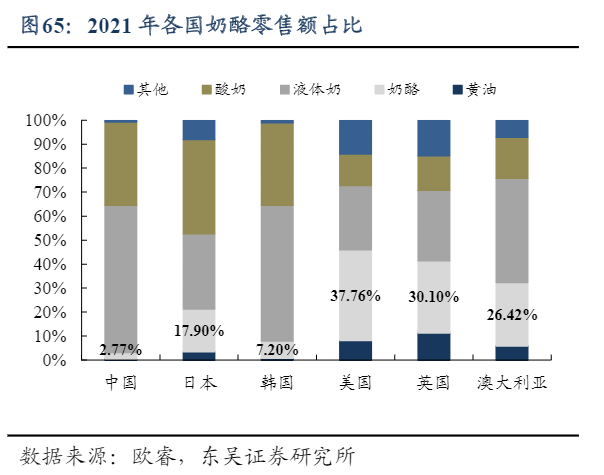
图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度。
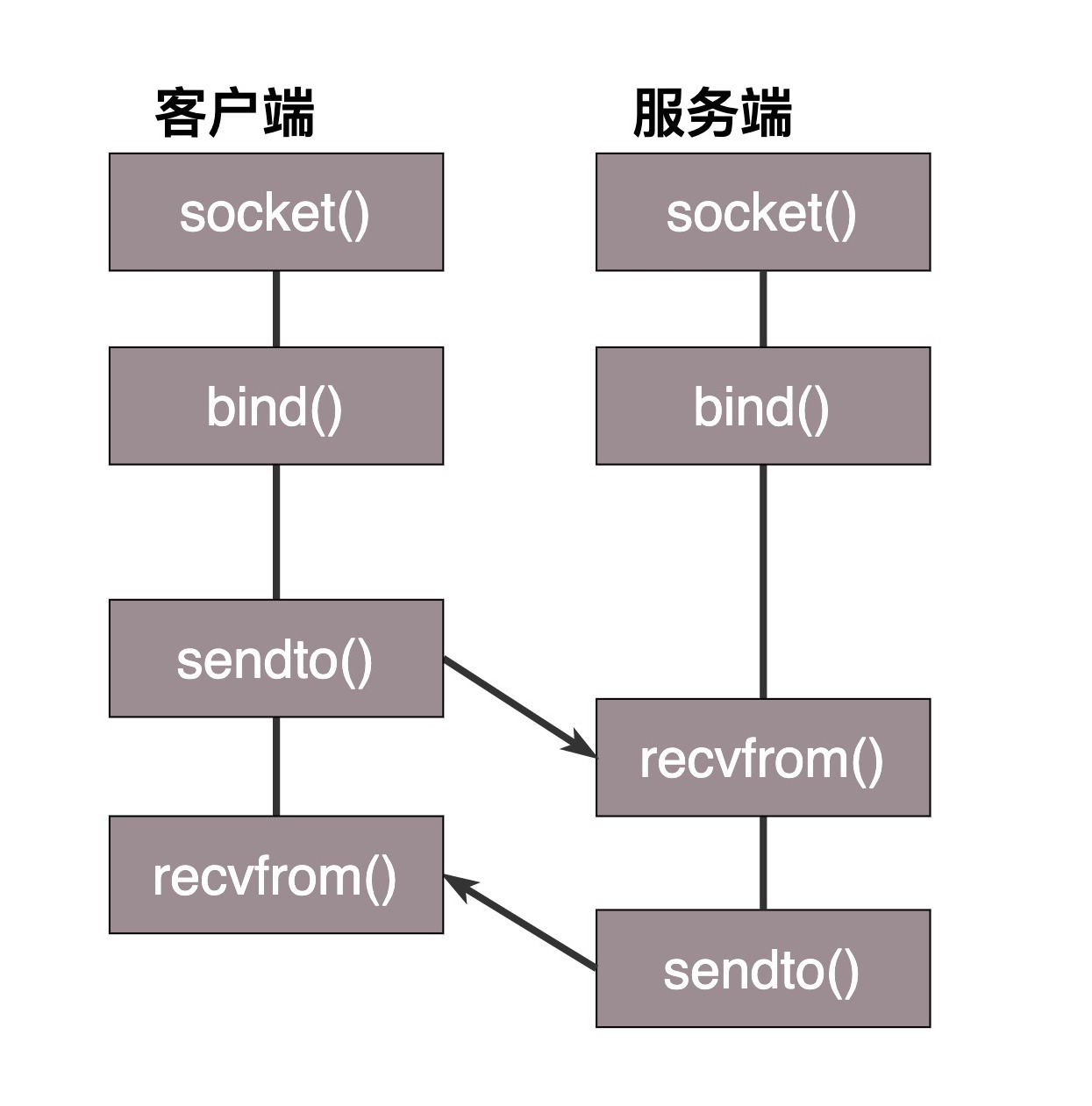
从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。
梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。
Fourier Analysis

amplitude 振幅
frequency 频率
phase 相位
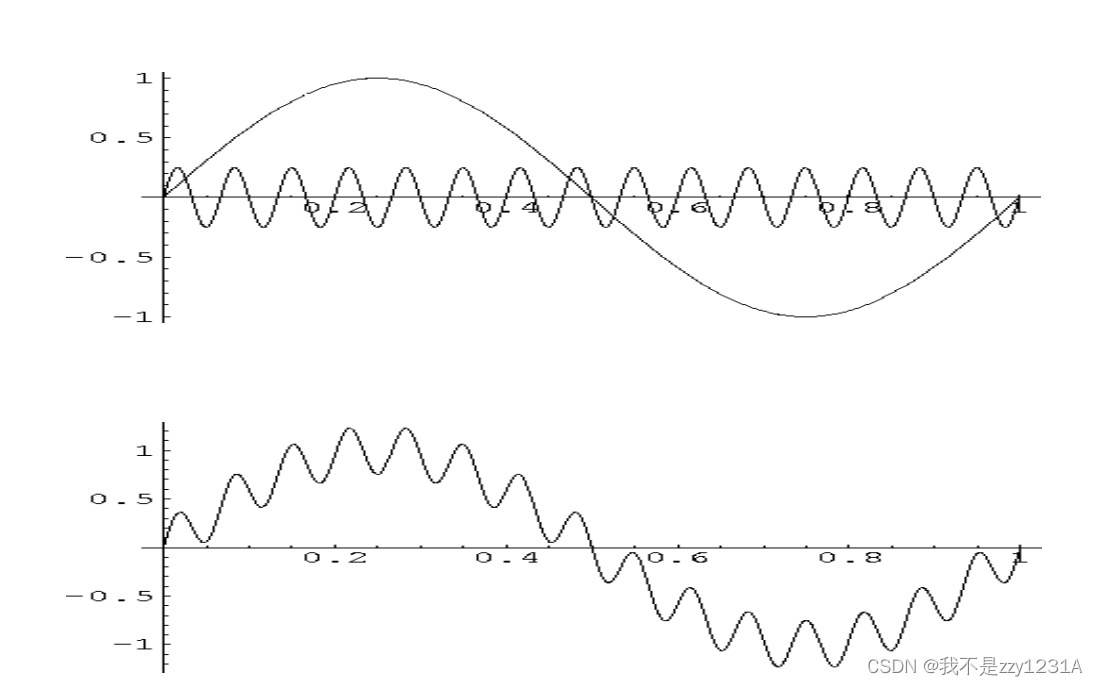
superposition 叠加

不同相位
傅里叶变换
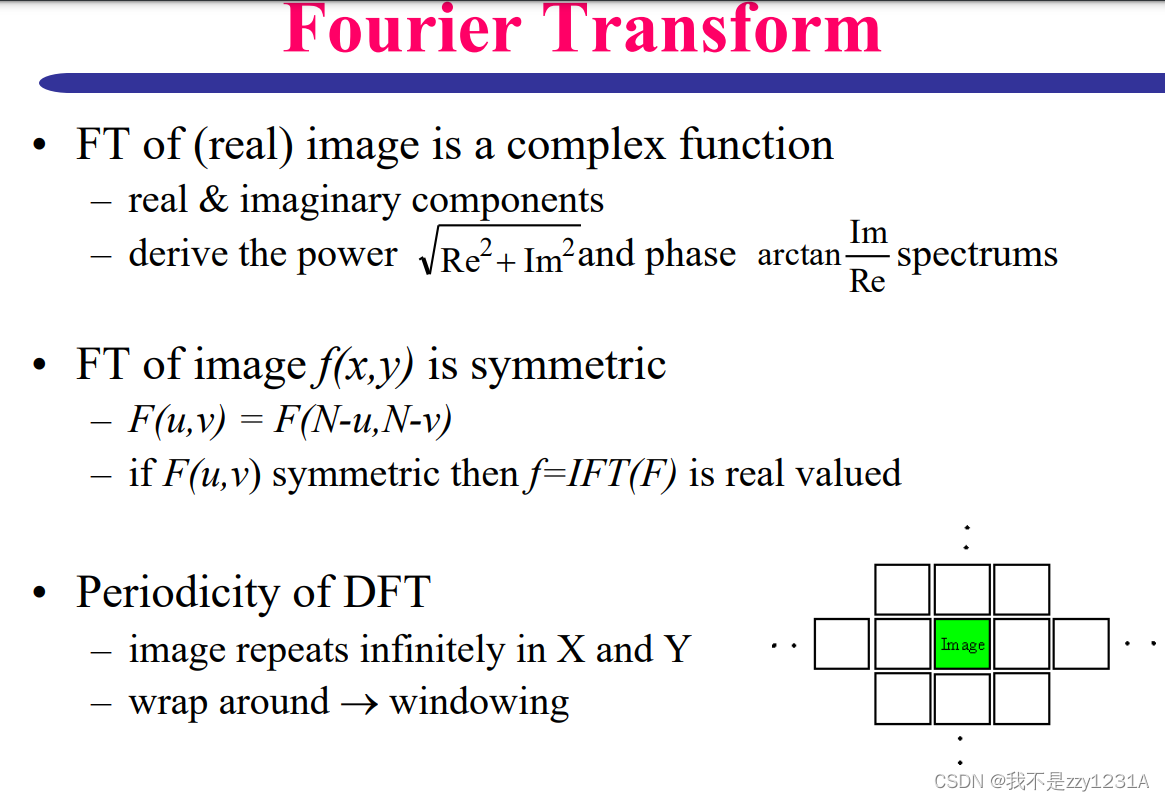

2D傅里叶基函数
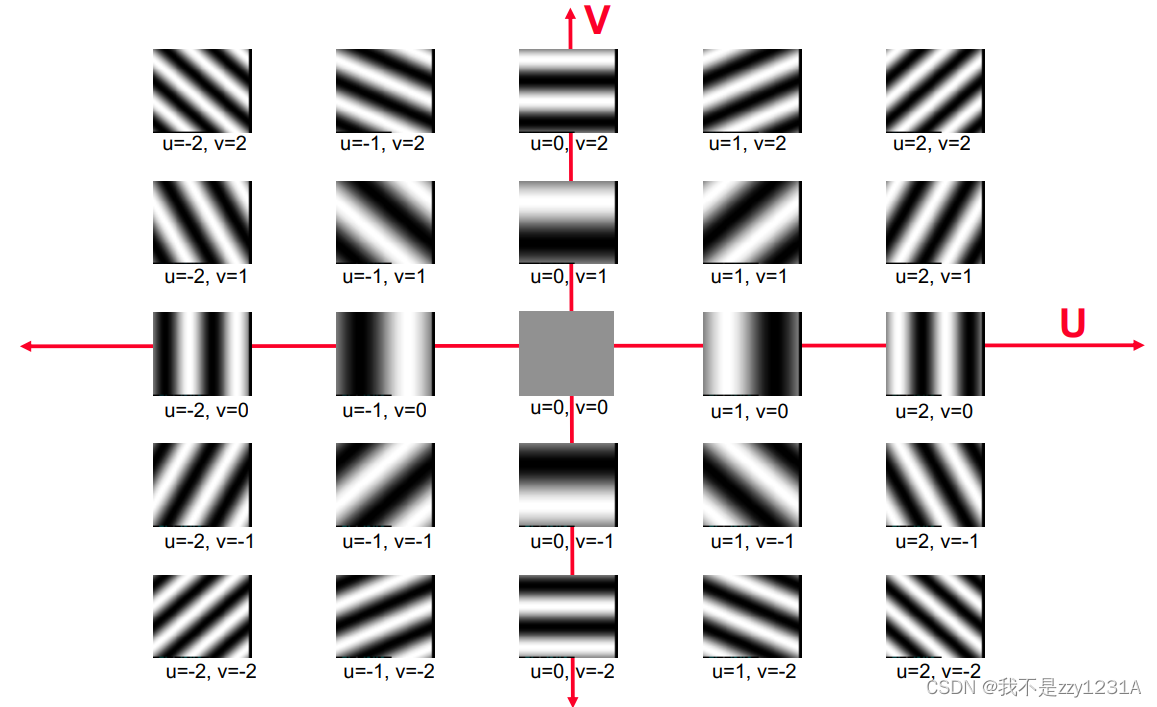

参考https://blog.csdn.net/weixin_40710375/article/details/94589706

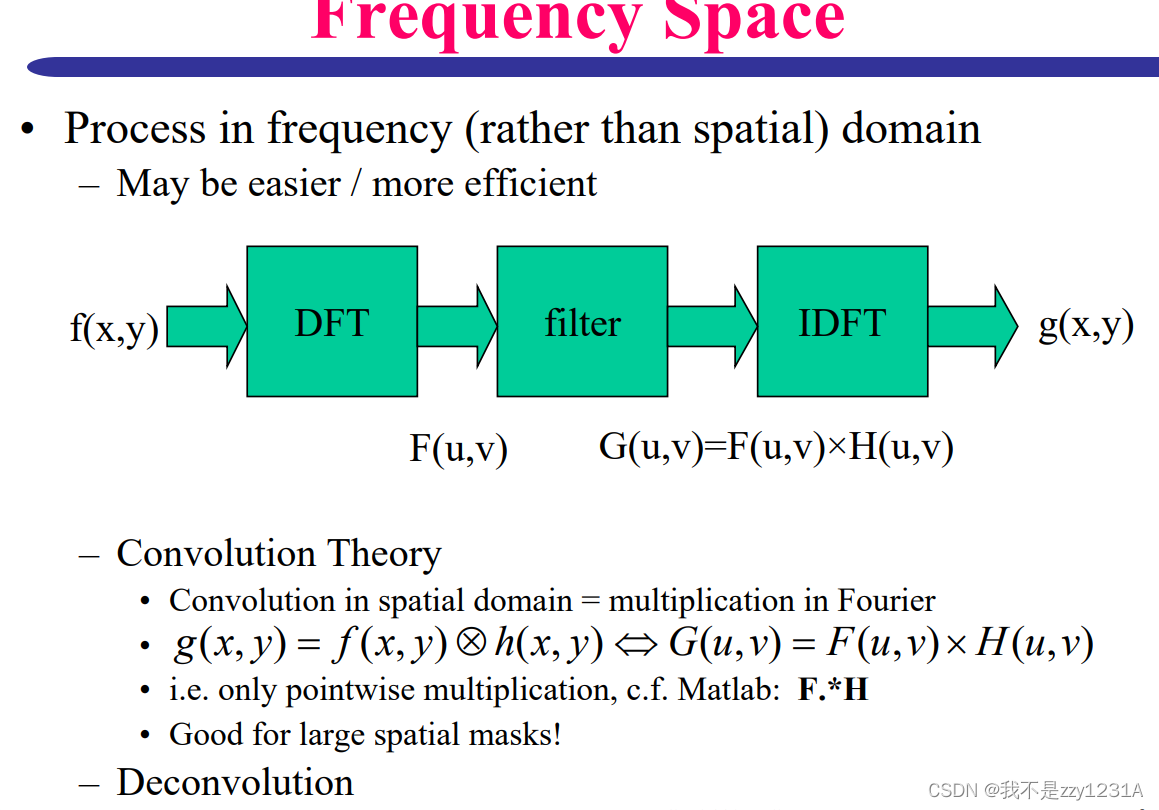
图像恢复


傅里叶描述子

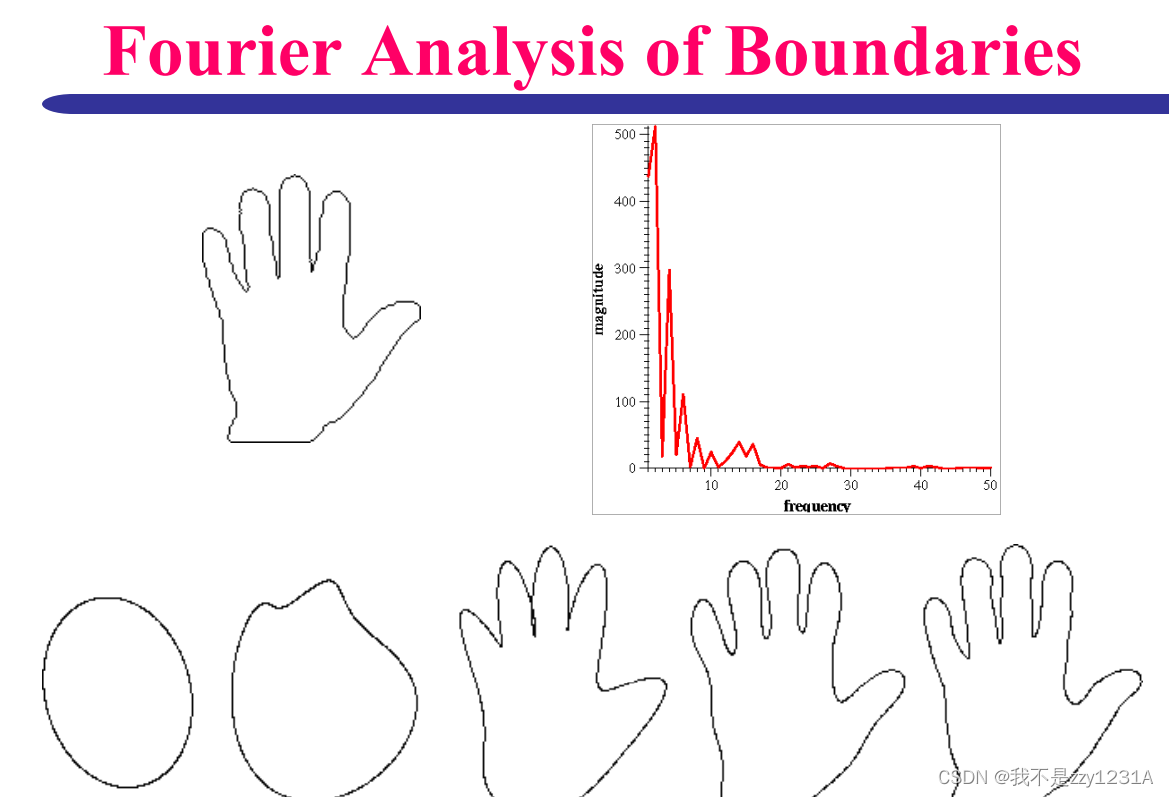
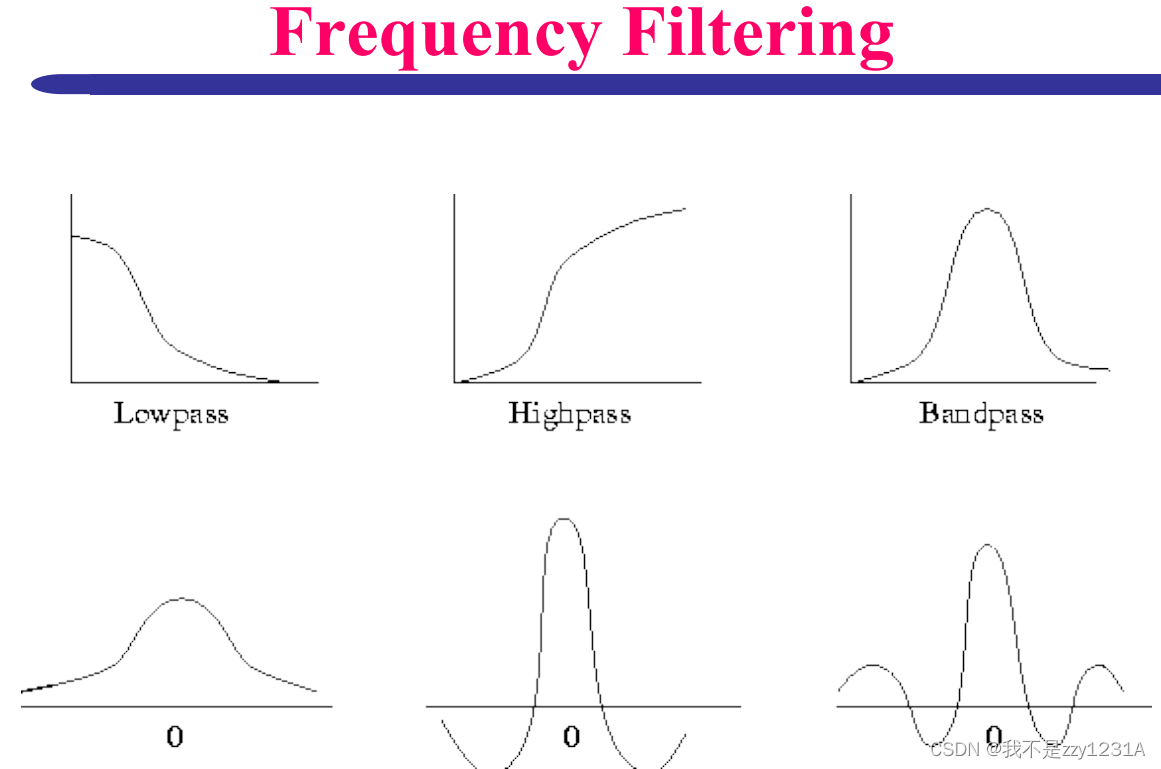
后面的重点去看
空间谱变频谱 去除某一频率 削减了灰度变化最不剧烈的部分
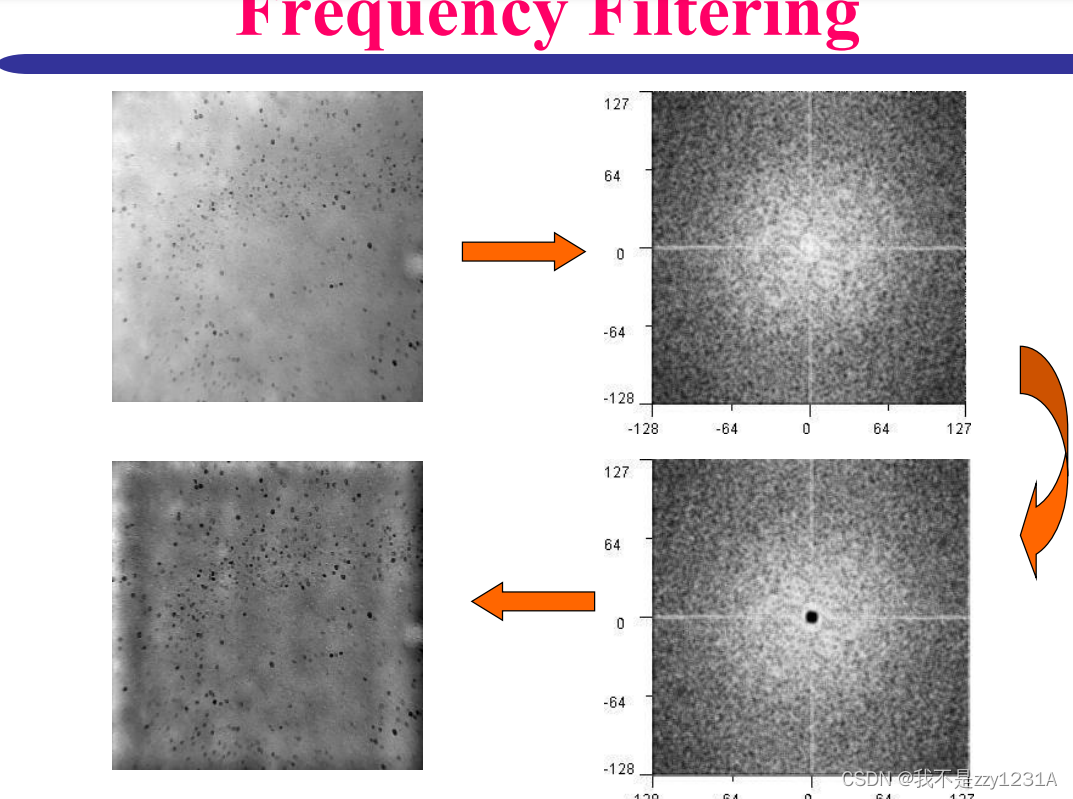
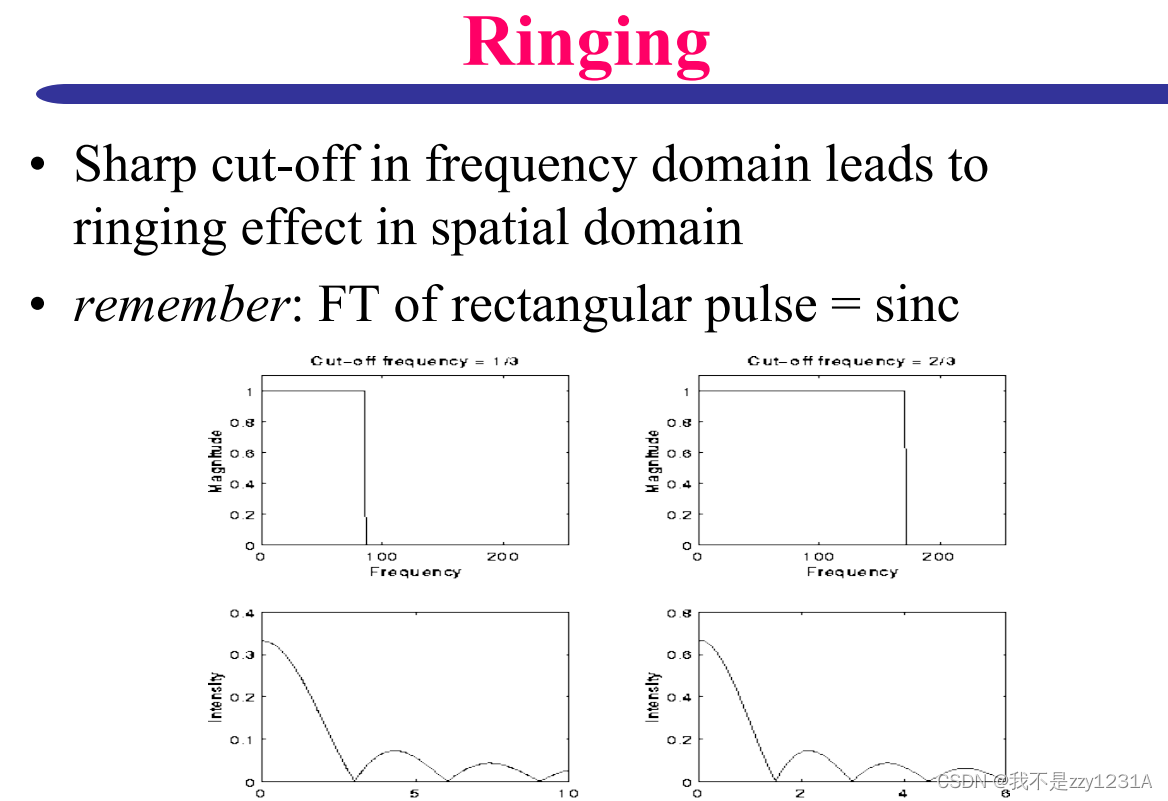
ringing震荡
频域中的急剧截止导致空间域中的震荡效应
缺少100之后的灰度变化的剧烈程度 只有较低剧烈程度变化的灰度变化 出现空间域震荡
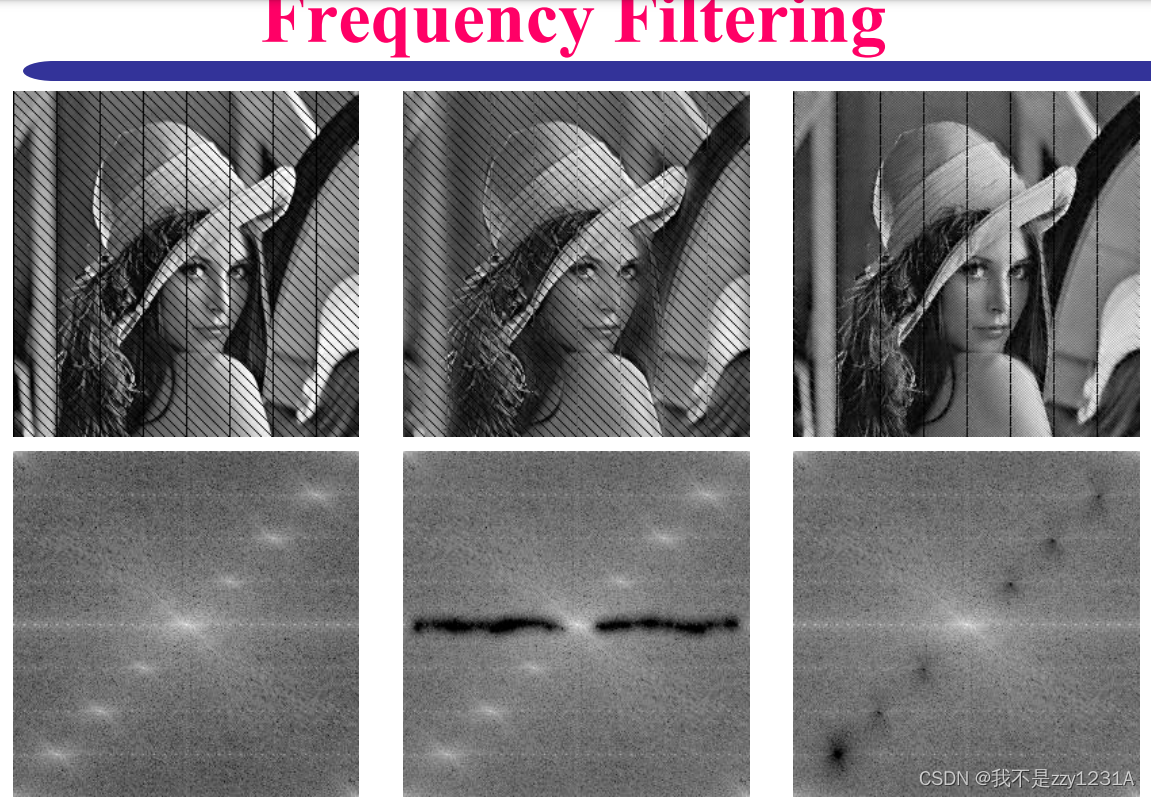
不是很懂这个图

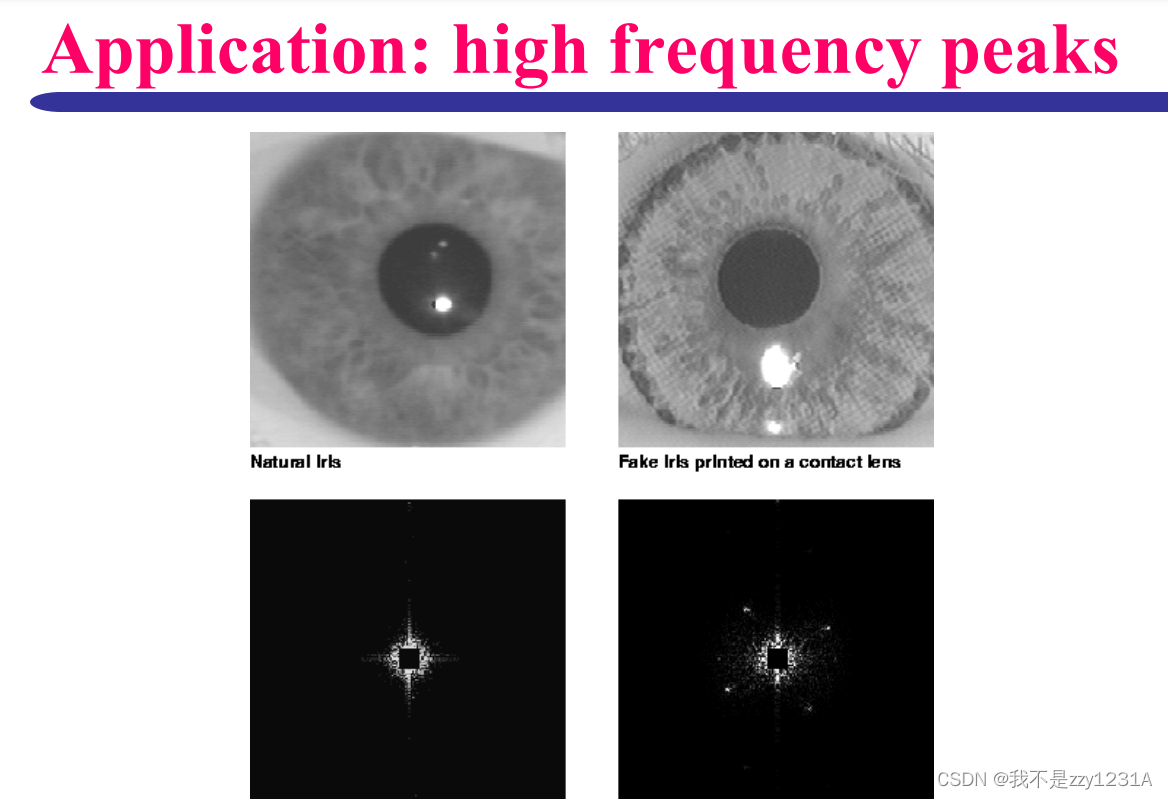
高频峰值

一些滤波
纹理分析

matlab试一下
https://blog.csdn.net/songzitea/article/details/16344441?ops_request_misc=&request_id=&biz_id=102&utm_term=%E5%82%85%E9%87%8C%E5%8F%B6%E5%88%86%E6%9E%90%20%E5%9B%BE%E5%83%8F%E5%A4%84%E7%90%86&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduweb~default-0-16344441.142v71insert_chatgpt,201v4add_ask&spm=1018.2226.3001.4187