A - Count Down
输出小于等于$n$的数
代码

B - Sandwich Number
题意 问字符串是否是第一个和最后一个字符是大小写，中间的字符是$100000-99999$之间的数字。
暴力模拟即可，需要注意的例子是$A0100000A$
代码

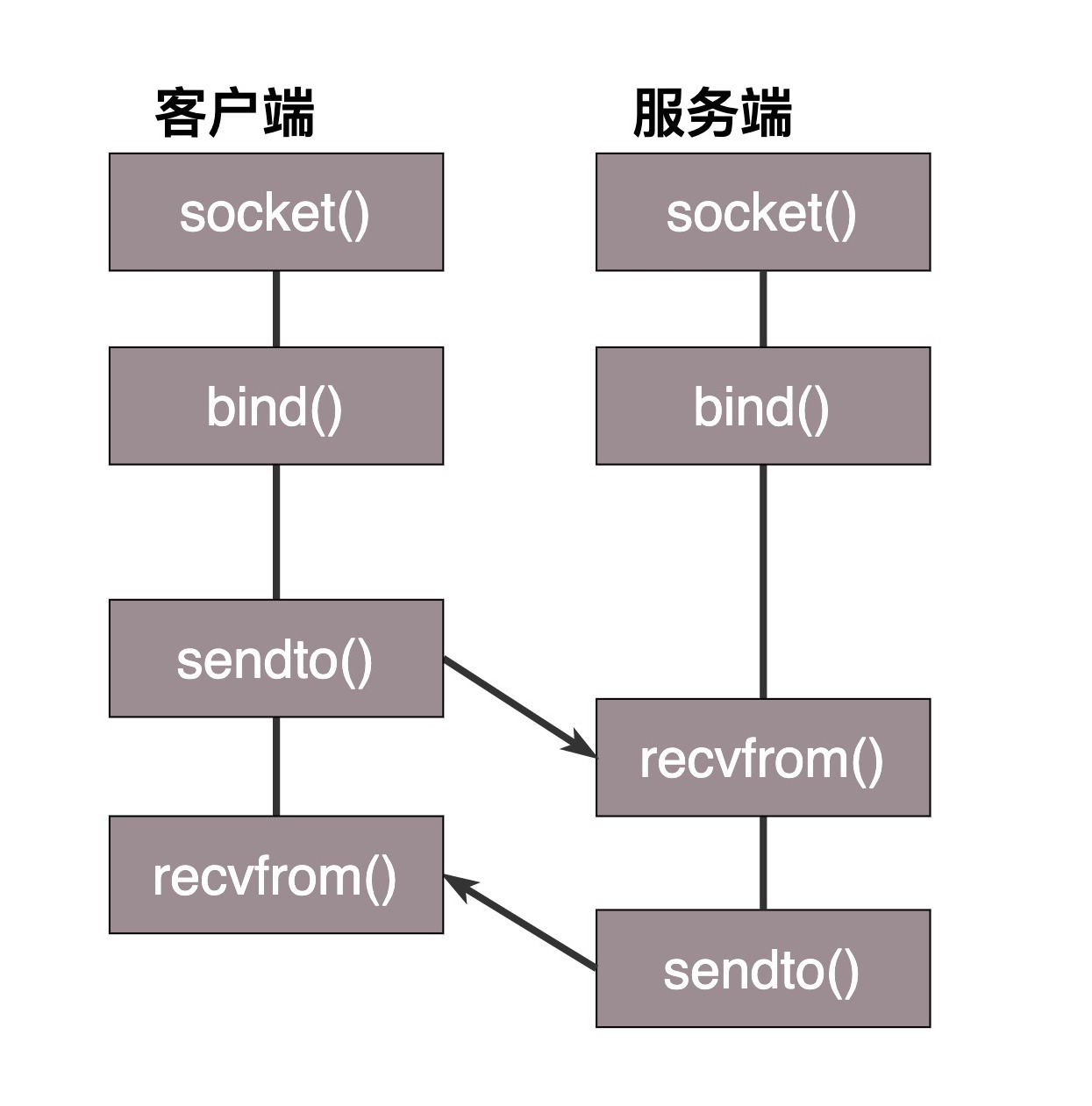
C - Circular Playlist
题意 给你一个循环的时间安排表，给你时间，问你最后在哪个活动，做了多长时间。
考察了取模，取模后看看模数在哪个活动即可
代码

D - Max Multiple
题意 给你n个数，选k个数能组成d的最大倍数，问这个倍数为多少
思路：考虑dp，我们把d的倍数看成对$d$取模为0,然后转化为模数问题，然后暴力dp即可。
代码

E - Least Elements
题意 问你所有长度为$m$的区间前k个数的和并打印出来。
思路 两种做法
1.对顶堆暴力判断，我们每次把在区间外的删除，然后加到一个堆上，调整堆，让第一个堆的大小为$k$
即可。
调整思路： 如果第一个堆的大小小于k，我们从第二个堆最小的一个一个拿过来，大于k的话就把第一个堆最大的数一个一个放到第二个堆即可，代码也好些，思路比较好想。
2.树状数组模拟即可。
第二种思路代码

F - Xor Minimization
题意 给你一个$a$数组，任取$x$，求所有数的异或和最大的最小值。
图例：

思路：看到异或自然想到拆位，很容易发现这是一道字典树方向的题目，继续思考，发现一个性质，考虑在字典树上dfs，因为当我们选择了$x$这一位取0时，我们可以显而易见的发现，这一位为0的一定不可能为最大值，我们就往1上遍历 (完全不用考虑0子树的情况) 。仔细推敲可以发现一种比较好写的写法。
我们遍历字典树的时候，如果这个子树(考虑小于等于$k$位的情况)如果两个子树($0$子树和$1$子树)都存在的话，那我们往哪递归都一定让答案第$k$为1，有一个子树为空，答案可以走到不为空的子树让答案为0，暴力dfs即可。
我写了一种比较好写的递归，核心代码如下

void dfs(int u , int k , int ans){
	if(k == -1) {
		tot = min(ans , tot) ; 		
	}
	else {
		if(son[u][0]) 
			dfs(son[u][0] , k - 1 , ans | ((son[u][1] != 0) << k) ) ;
		if(son[u][1])
			dfs(son[u][1] , k - 1 , ans | ((son[u][0] != 0) << k) ) ; 
	}
}

代码

G - Farthest City
vp时没时间去写这道题了，但是想到了一个很好想而且非常好实现的代码，由于本人懒没有写 ，接下来就是口胡思路 。

题意
给你一个大小为$n$的子树，问你图的数量，图满足1到除$n$之外的点都严格小于$n$
思路 看到这个题，首先一个比较快的想法是要先建树，与最短路相关的树就是最小路径树，我们考虑最小路径树的建立方式，我们为了不会重复计数，我们可以一层一层地有标号计数去统计答案，由于题目要求的是图的数量，我们肯定会存在非树边，手玩也可以发现非树边一定是在同一层或相邻层之间的两个节点之间建立的，也是一种横叉边的说法，这个时候用到了相邻层的数量，所以考虑维护当前层和相邻层的数量，$dp$的建立方式也就出来了，我们考虑$dp$为当前已经包含了$n$个节点，上一层有$m$个节点，当前层有$k$个节点的方案数，值得需要注意的是我们第$n$个点一定最后加而且一定加到层的最后面。
然后考虑$dp$转移，我们dp转移考虑两个方面
1.加到当前层$dp[n][m][k]$肯定是由$dp[n][m][k-1]$转移过来，然后可以选择的操作是，加到当前层一定是由上一层转移过来，我们可以选择上一层的多个节点(不能为0)连接起来，方案数是 2ⁿ - 1 ,减去了都不选的情况。同一层的我们可以选择若干条连接(可以为空) , 方案数为 2ⁿ，然后就是标号的选择是$N$-$n$。
2.如果考虑成为最高的一层(加到当前最大的一层），转移为$dp[n][m][1]$,由dp[n][k][m]转移过来，这一步转移是$O(m)$的过程,总共只有$O(n^2)$次不影响时间复杂度。然后非树边的连接方式类似。
最后考虑$n$的连接和上述的第二步类似，直接输出方案即可。