1. 连杆码垛机械臂介绍
连杆码垛机器人是工业应用场景中常用的一种机械臂,常用于简单的大负载搬运作业场景。常见的连杆码垛机械臂都是4个自由度,相较于6轴和7轴的机械臂成本较低。

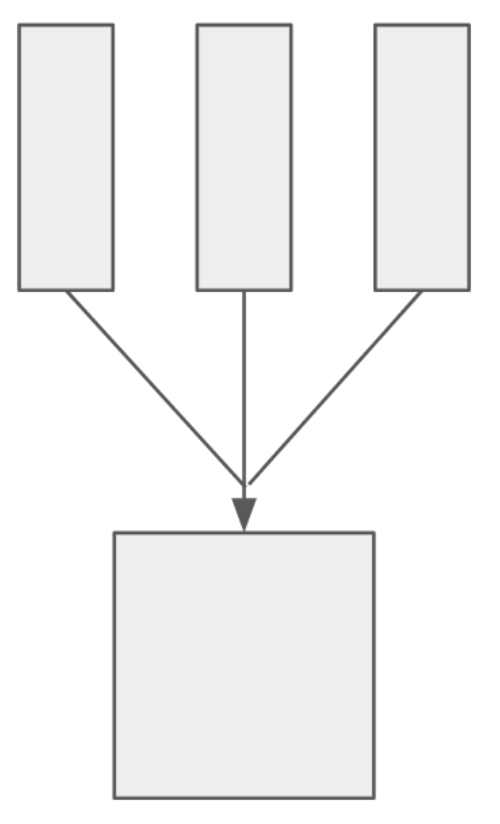
连杆码垛机械臂的运动特性是:末端始终平行于地面。第一个平行四边形:ABDE,第二个平行四边形:EFGH,通过两个平行四边形的作用,位于H点的末端始终保持平行于AB,如图结构平行于地面:

2. 运动学反解计算
机器人运动学就是根据末端执行器与所选参考坐标系之间的几何关系,确定末端执行器的空间位置和姿态与各关节变量之间的数学关系。包括正运动学(Forward Kinematics)和逆运动学(Inverse Kinematics)两部分。
正运动学就是根据给定的机器人的各个关节变量,计算末端执行器的位置和姿态。
反解(逆向运动学)则是根据已知的末端执行器的位置和姿态,计算机器人各个关节变量,也被称为机器人运动学求解。
关节变量 —–> 机械臂末端执行器的姿势 = 正向运动学
机械臂末端执行器的位姿 —–> 关节变量 = 逆向运动学
基本步骤:
(1)确定关节、连杆及其参数 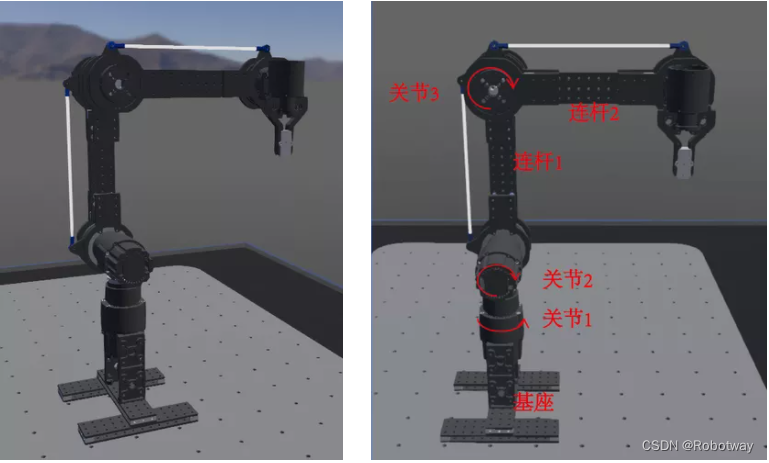
(2)简化模型设定坐标系为方便计算:
(a)由转台和大臂关节轴线交点为原点;
(b)以竖直向上为+Z轴;
(c)以大臂关节轴线为Y轴;
(d)以垂直Y0Z平面且交于O点为X轴;

这里我们设定:已知B点坐标为(x,y,z),OA为大臂长度=L1,OB为小臂长度=L2
我们需要求解:1.转台转动角度;2.大臂转动角度;3.小臂转动角度
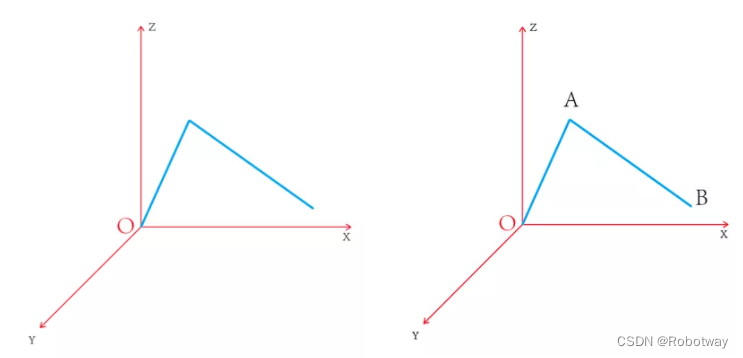
从俯视图可看出我们需要求解的转台角度θ

投影于机械臂大臂和小臂所在平面后,可得出:需求解大臂转动角度α,小臂转动角度β
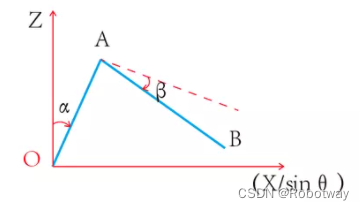
求解转台角度θ:

求解大臂角度α:


求解小臂角度β:
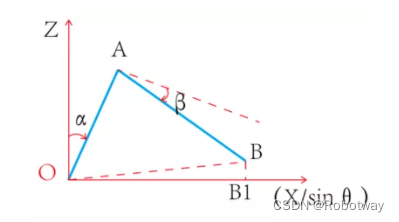


以上计算方法和过程,可以基于Webots构建出来,了解详情请观看视频或下载资料。
讲解视频2:全程干货【连杆码垛机械臂运动学解算】
3.资料内容
① 连杆码垛机械臂逆运动学讲解.pptx
② 仿真项目源代码
③ 电机驱动函数库
资料内容下载详见 如何实现机械臂的逆解计算