Introduction to Multi-Armed Bandits——02 Stochastic Bandits

参考资料

1. Slivkins A. Introduction to multi-armed bandits[J]. Foundations and Trends® in Machine Learning, 2019, 12(1-2): 1-286.

2. 在线学习(MAB)与强化学习(RL)[2]：IID Bandit的一些算法

Bandit算法学习[网站优化]偏实战，而本专栏偏理论学习。

本章介绍具有独立同分布奖励的bandit，这是MAB的基本模型。我们提出了几种算法，并从悔值的角度分析了它们的性能。

一、模型和实例

我们考虑具有独立同分布奖励的基本模型，称为stochastic bandits。一个算法有 $K$ 个可能的动作可供选择，即臂(arm)，有 $T$ 个回合, $K$ 和 $T$已知。在每一轮中，算法选择一只臂，并为这只臂收集奖励。该算法的目标是在 $T$ 轮中最大化其总回报。我们做了三个基本假设：

• 该算法只观察所选动作的奖励，而不观察其他。特别是，它没有观察到本可以选择的其他动作的奖励。这就是所谓的bandit feedback。

• 每次行动的奖励是独立同分布的。对于每个动作 $a$ ，在实数域上有一个分布 $D_a$，称为 reward distribution。每次选择此动作时，奖励都会独立于此分布进行采样。该算法最初不知道奖励分布。

• 每轮奖励是有限制的;出于简化。限制在区间[0，1]。

因此，算法根据下面总结的协议进行交互。

我们主要关注mean reward vector（平均奖励向量）$\mu \in [0,1{]}^K$，其中$\mu (a)=\mathbb{E}[D_a]$是臂 $a$ 的平均奖励。也许最简单的奖励分布是伯努利分布：每个臂 $a$ 的奖励可以是1或0(“成功或失败”，“正面或反面”)。这种奖励分布完全由平均奖励决定，在这种情况下，平均奖励就是成功结果的概率。然后，问题实例完全由时间范围 $T$ 和平均奖励向量指定。

我们的模型是对现实的一个基本特征的简单抽象，它存在于许多应用场景中。接下来我们将举三个例子:

1. 新闻：在一个非常程式化的新闻应用程序中，用户访问一个新闻站点，该站点显示一个新闻标题，用户可以单击这个标题，也可以不单击。网站的目标是最大限度地增加点击量。所以每个可能的标题都是bandit问题中的一个臂，点击就是奖励。每个用户都是从用户的固定分布中独抽取的，因此在每一轮中，点击都是独立发生的，其概率仅取决于所选的标题。

2. 广告选取：在网站广告中，用户访问网页，算法从许多可能的广告中选择一个来显示。如果显示广告$a$，则网站观察用户是否点击该广告，在这种情况下，广告商支付一定的金额$v_a\in [0,1]$。因此，每个广告都是一只臂，支付的金额就是奖励。$v_a$仅取决于所显示的广告，但不随时间改变。给定广告的点击概率也不会随时间变化。

3. 医学实验：病人去看医生，医生可以从几种可能的治疗方法中选择一种，并观察治疗效果。然后下一个病人过来，以此类推。为了简单起见，治疗的有效性被量化为$[0,1]$的数字。每一种治疗都可以被认为是一只臂，而奖励则被定义为治疗效果。作为一个理想化的假设，每个患者都是从固定的患者分布中独立抽取的，因此给定治疗的有效性是独立同分布的。

请注意，在前两个示例中，给定臂的奖励只能接受两个可能的值，但在第三个示例中，原则上可以接受任意值。

备注: 我们在本章和本书的大部分内容中都使用了以下约定。我们将交替使用臂和动作。

• 臂用$a$表示，轮次用$t$表示。有$K$个臂和$T$轮。
• 所有臂的集合是$\mathcal{A}$。每只臂的平均报酬是$\mu (a):=\mathbb{E}[D_a]$.
• 最佳平均报酬用 ${\mu }^{\ast }:={\max }_{a\in \mathcal{A}}\mu (a)$表示。
• 差值为$\Delta (a):={\mu }^{\ast }-\mu (a)$
  描
• 述了臂 $a$ 与${\mu }^{\ast }$相比差多少; 我们称之为臂 $a$ 的 $gap$ 。
• 最优臂是臂$a$ 有 $\mu (a)={\mu }^{\ast }$，而最优臂不是唯一的。我们用$a^{\ast }$ 表示某个最优臂。
• $[n]$ 表示集合 { 1 , 2 , ⋯   , n } \{1,2 ,\cdots, n\} {1,2,⋯,n}。

Regret(悔值)

• 我们如何论证一个算法在不同的问题实例中是否做得很好?一种标准方法是将算法的累积奖励与best-arm基准 ${\mu }^{\ast }\cdot T$(总是选择最优臂的期望奖励)进行比较。形式上，我们定义了在轮次$T$上的悔值(regret):

$$\begin{array}{r}R(T)={\mu }^{\ast }\cdot T-\sum _{t=1}^T\mu (a_t).\end{array}\text{\hspace{1em}(2.1)}$$

事实上，这就是算法“后悔”没有提前知道最佳臂的程度。请注意，$a_t$，在$t$处选择的臂，是一个随机量，因为它可能取决于奖励和/或算法的随机性。$R(T)$也是一个随机变量。我们通常会谈论$期望悔值\mathbb{E}[R(T)]$

主要关心$\mathbb{E}[R(T)]$ 悔值在时间范围$T$上的依赖关系。还考虑了对臂数量$K$和平均奖励$\mu (\cdot )$的依赖。对奖励分布的细粒度依赖不太感兴趣。通常使用big-O表示法来关注对所关注参数的渐近依赖关系。

备注(术语): 由于对悔值的定义是对所有回合的总和，我们有时称之为累积悔值（cumulative regret）。当我们需要突出$R(T)$和$\mathbb{E}[R(T)]$之间的区别时，我们说现实悔值（realized regret）和期望悔值（expected regret）;但大多数时候，我们只是说“悔值”，从上下文来看，意思很清楚。数量$R(T)$在文献中有时被称为伪悔值（pseudo-regret）。

二、简单算法：uniform exploration

我们从一个简单的想法开始：统一探索（explore）臂（以相同的速度），而不管之前观察到的情况如何，并选择经验上最好的手臂进行利用（exploit）。这个想法对应的算法，称为 $Explore-first$ 算法：将初始轮段专门用于探索，其余轮用于利用。

参数$N$是预先固定的;它将根据时间$T$和臂数量$K$进行选择，以减少悔值。让我们来分析一下这个算法的悔值。

让每个动作$a$在探索阶段后的平均奖励表示为$\bar{\mu }(a)$。我们希望平均奖励是对真实预期奖励的良好估计，即$|\overline{\mu }(a)-\mu (a)|$应该很小。我们用Hoeffding不等式来约束它：

$$\begin{array}{r}\text{Pr}\left[|\overline{\mu }(a)-\mu (a)|\le \text{rad}\right]\ge 1-\frac{2}{T^4}\text{, where }\text{rad}:=\sqrt{2\log (T)/N}\end{array}\text{\hspace{1em}(2.2)}$$

因此，$\mu (a)$ 以高概率位于已知区间 $\left[\overline{\mu }(a)-\text{rad},\overline{\mu }(a)+\text{rad}\right]$
中。 一个包含某个标量的已知区间称为该标量的置信区间($confidenceinterval$)。这个区间长度(本例中为rad)的一半称为置信度( $confidenceradius$ )。

在不知道 $\mu (a)$ 的情况下，采集了 $N$ 个样本之后，我们用样本平均值进行估计，这个估计对于 $\mu (a)$ 的误差大概是 $\sqrt{\log T/N}$ 级别的。同时，因为我们一般可以认为我们的分析是渐进(asymptotic)的，我们可以认为 $T$ 非常大，因此这件事情发生的概率非常高（ $2/T^4\to 0$ ）

将$cleanevent$定义为（1.2）对所有臂同时成立的事件。我们将分别论证$cleanevent$和 “$badevent$”——$cleanevent$的补充。有了这种方法，我们就不需要在剩下的分析中担心概率问题。

为了简单起见，让我们从$K=2个$臂的情况开始。考虑一下$cleanevent$:

让最佳手臂为$a^{\ast }$，假设算法选择了另一个手臂$a\ne a^{\ast }$。这一定是因为它的平均奖励比$a^{\ast }$的好。$\bar{\mu }(a)>\bar{\mu }(a^{\ast })$。

$$\begin{array}{r}\mu (a)+\text{rad}\ge \bar{\mu }(a)>\bar{\mu }(a^{\ast })\ge \mu (a^{\ast })-\text{rad}\end{array}$$

可得到 $\mu (a^{\ast })-\mu (a)\le 2\text{rad}$

因此，利用阶段的每个回合最多产生 $2\text{rad}$ 的悔值。探索阶段的每一轮最多产生$1$。

$$\begin{array}{r}R(T)\le N+2\text{rad}\cdot (T-2N)<N+2\text{rad}\cdot T\end{array}$$

回忆一下，我们可以选择$N$的任何值。因此，我们可以选择（近似）最小化右值的$N$。由于两个总和在$N$中分别是单调递增和单调递减的，我们可以设置$N$使它们近似相等。对于$N=T^{2/3}(\log T{)}^{1/3}$。得到：

$$\begin{array}{rl}R(T)& \le O\left(T^{2/3}(\log T{)}^{1/3}\right)\end{array}$$

剩下的就是分析 "$badevent$ "。由于悔值最多只有$T$（每轮最多贡献$1$），而$badevent$发生的概率非常小，因此可以忽略这一事件的悔值。从形式上看：
$$\begin{array}{rl}\mathbb{E}\left[R(T)\right]& =\mathbb{E}\left[R(T)\mid \text{clean event}\right]\times \mathrm{Pr}\left[\text{clean event}\right]+\mathbb{E}\left[R(T)\mid \text{bad event}\right]\times \mathrm{Pr}\left[\text{bad event}\right]\\ & \le \mathbb{E}\left[R(T)\mid \text{clean event}\right]+T\times O(T^{-4})\\ & \le O((\log T{)}^{1/3}\times T^{2/3})\end{array}\text{\hspace{1em}(2.3)}$$

对于$K>2$的臂，我们在$K$个臂上应用（2.2）的联合约束。然后遵循上述相同的论证。请注意，$T\ge K$ 不失一般性，因为我们需要对每个臂至少探索一次。对于最后的悔值计算，我们需要考虑到对$K$的依赖性：具体来说，探索阶段积累的悔值被$KN$所限制了。通过证明，我们得到$R(T)\le NK+2\text{rad}\cdot T$。和以前一样，我们通过近似最小化两个总和来近似最小化它。插入 $N=(T/K{)}^{2/3}\cdot O(logT{)}^{1/3}$。以与（2.3）相同的方式完成证明，得到：

定理2.5：$\text{Explore-first achieves regret}\mathbb{E}\left[R(T)\le T^{2/3}\times O(K\log T{)}^{1/3}\right]$

2.1 改进：Epsilon-greedy算法

$Explore-first$ 的一个问题是，如果许多/大多数臂有很大的差距 $\Delta (a)$，那么它在探索阶段的表现可能非常糟糕。一般将探索更均匀地分布在时间上会更好。这种思想应用在了$Epsilon-greedy$算法。

在短期内选择最佳选项在计算机科学领域中被称为"贪婪"（greedy）选择，因此该算法得名"Epsilon-greedy"。探索在臂上是均匀的，类似于探索优先算法中的"轮循"（round-robin）探索。由于探索现在是随着时间均匀地传播的，所以即使对于小的 $t$，也可以希望得到有意义的悔值边界。我们关注探索概率 ${ϵ}_t\sim t^{-1/3}$ (暂时忽略对 $K$ 和 $\log t$ 的依赖)，使得探索轮次的期望值是 $t^{2/3}$ 的量级，这与时间跨度为$T=t$的 $Explore-first$ 算法相同。推导出与定理2.5相同的悔值界，现在它对所有轮次 $t$ 都成立。

定理1.6: 探索概率为 ${ϵ}_t=t^{-1/3}\cdot (K\log t{)}^{1/3}$ 的 Epsilon-greedy 算法在轮次 $t$ 中达到的悔值界为 $\mathbb{E}[R(t)]\le t^{2/3}\cdot O(K\log t{)}^{1/3}$ 。

2.2 非适应性探索

$Explore-first$ 和 $Epsilon-greedy$ 不会调整他探索计划，以适应观察到的奖励的历史。我们将此属性称为非适应性探索（non-adaptive exploration,），并将其形式化表述如下：

定义1.7：如果轮次 $t$ 的数据 $(a_t,r_t)$ 被算法用于未来的回合，那么这个轮次就是一个探索轮次（exploration round）。如果所有探索轮的集合和其中的臂选择在第 $1$ 轮之前是固定的，那么这个确定性算法就满足非适应性探索。如果一个随机算法对其随机种子的每一次实现都能满足非适应性探索，则该算法满足非适应性探索。

接下来，我们通过根据观察结果调整探索，来获得更好的悔值界限。

三、高级算法：自适应探索

我们提出了两种算法，它们取得了更好的悔值界限。这两种算法都是根据观察结果来调整探索，从而使表现很差的臂更早地被淘汰。

让我们从 $K=2$ 个臂的情况开始。一个自然的想法是这样的：

$$不断轮换臂，直到我们确信哪只臂更好，然后使用这只臂。\text{\hspace{1em}(2.4)}$$

接下来进行具体的说明。

3.1 Clean event and confidence bounds

固定轮次 $t$ 和臂 $a$。让 $n_t(a)$ 为 $t$ 之前选择此臂的轮次数，让 ${\bar{\mu }}_t(a)$ 为这些轮次的平均奖励。我们将使用Hoeffding不等式来推导出如下公式：

$$\begin{array}{r}\mathrm{Pr}\left[|{\bar{\mu }}_t(a)-\mu (a)|\le r_t(a)\right]\ge 1-\frac{2}{T^4},\text{where}{r}_t(a)=\sqrt{2\log (T)/n_t(a)}\end{array}\text{\hspace{1em}(2.5)}$$

然而，上式并不能立即得到。这是因为Hoeffding不等式只适用于固定数量的独立随机变量，而这里我们来自奖励分布 ${\mathcal{D}}_a$ 的 $n_t(a)$ 个随机样本，，其中$n_t(a)$ 本身是一个随机变量。此外，$n_t(a)$ 可能取决于手臂 $a$ 过去的奖励，所以在$n_t(a)$ 的特定实现的条件下，$a$ 的样本不一定是独立的。 举个简单的例子，假设一个算法在前两轮中选择了手臂 $a$ ，当且仅当在前两轮中奖励为 $0$ 时在第3轮中再次选择它，并且不再选择它。

因此，我们需要一个更严谨的论证。我们提出这个论证的一个基本版本。对于每个臂 $a$ ，让我们想象有一个 $rewardtape$ ：一个 $1\times T$ 的表格，每个单元都从${\mathcal{D}}_a$中独立采样，如下图所示。

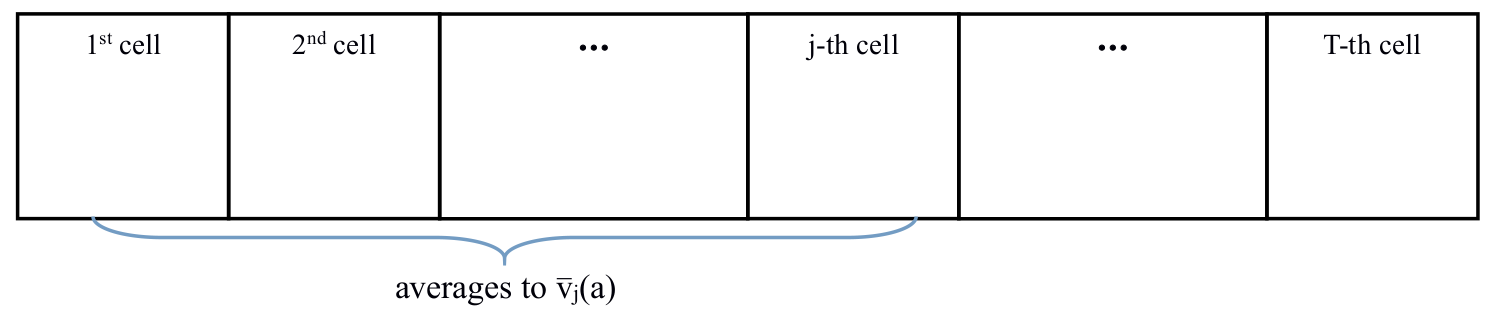
其中第 $j$ 个格子存储我们第 $j$ 次选择这个臂时观察到的奖励，用 ${\bar{v}}_j(a)$ 表示其平均值。使用Hoeffding不等式可推出：

$$\begin{array}{r}\forall j\mathrm{Pr}\left[|{\bar{v}}_j(a)-\mu (a)|\le r_t(a)\right]\ge 1-\frac{2}{T^4}\end{array}$$

通过联合约束，可以得出（假设 $K=\text{ \#arms }\le T$ ）

Pr ⁡ [ E ] ≥ 1 − 2 T 2 ,  where  E : = { ∀ a ∀ t ∣ μ ˉ t ( a ) − μ ( a ) ∣ ≤ r t ( a ) } \begin{align} \Pr\left[{\mathcal{E}}\right]\ge 1 - \frac{2}{T^2},\ \text{where}\ \mathcal{E} :=\{\forall a\forall t\quad |\bar{\mu}_t(a)-\mu(a)| \le r_t(a)\}\tag{2.6} \end{align} Pr[E]≥1−T22​, where E:={∀a∀t∣μˉ​t​(a)−μ(a)∣≤rt​(a)}​(2.6)​

其中 $\mathcal{E}$ 为 $cleanevent$。

对于每个臂 $a$ 在每轮 $t$ 中，我们定义一个置信上限和置信下限：

$$\begin{array}{rl}{\text{UCB}}_t(a)& ={\bar{\mu }}_t(a)+r_t(a),\\ {\text{LCB}}_t(a)& ={\bar{\mu }}_t(a)-r_t(a).\end{array}$$

置信区间为$\left[{\text{UCB}}_t(a),{\text{LCB}}_t(a)\right]$，置信度为$r_t(a)$

3.2 连续消除算法Successive Elimination algorithm

对于两个臂，使用置信界限，有如下算法：

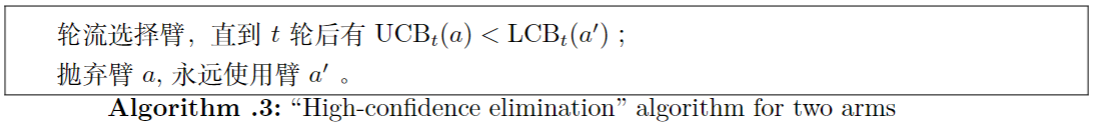
为了分析，假设是clean event。请注意，"被抛弃"的臂不可能是最好的臂。在取消一只臂的资格之前，我们要积累多少悔值？

让$t$为最后一轮，即两臂的置信区间仍然重叠时，如下图，则有
$$\Delta :=|\mu (a)-\mu (a^{\prime })|\le 2(r_t(a)+r_t(a^{\prime }))$$

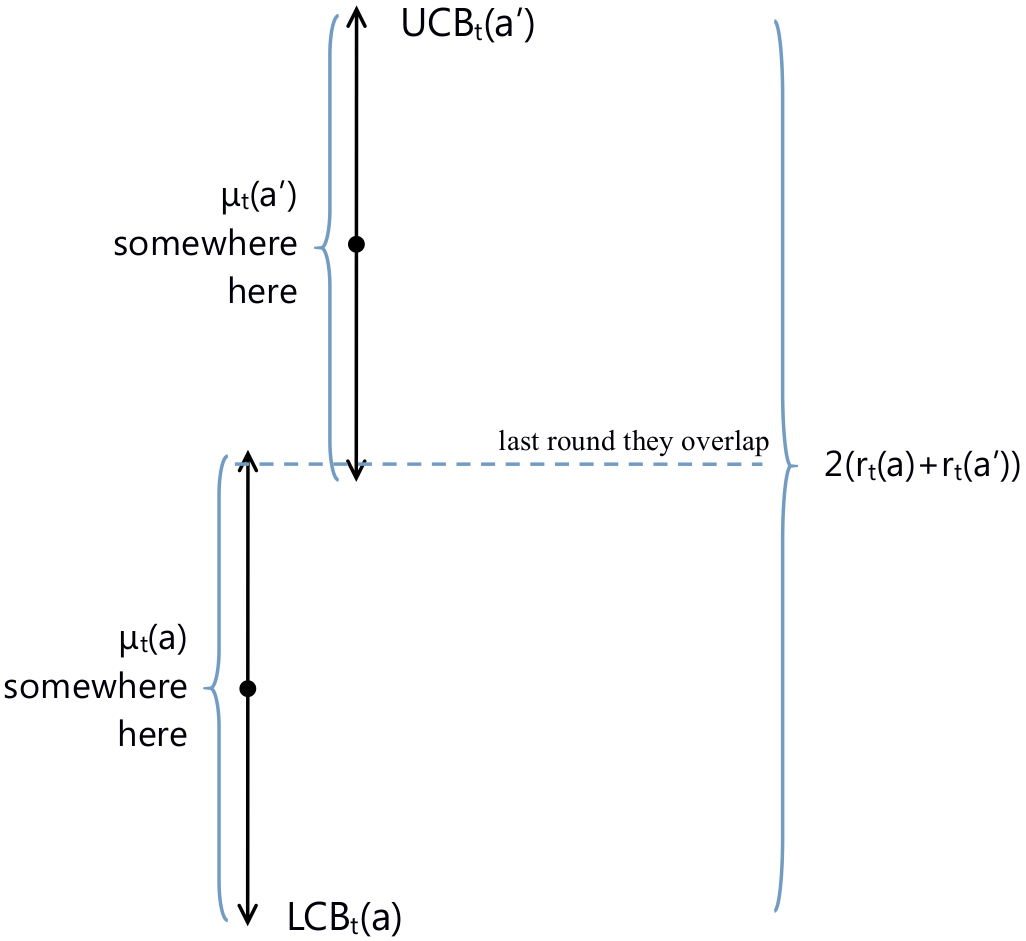
由于算法在时间 $t$ 之前一直在交替使用两臂，我们有 $n_t(a)=\frac{t}{2}$，可得到：

$$\Delta \le 2(r_t(a)+r_t(a^{\prime }))\le 4\sqrt{2\log (T)/\lfloor t/2\rfloor }=O(\sqrt{\log (T)/t})$$

$t$ 轮的悔值为：

$$R(t)\le \Delta \times t\le O\left(t\cdot \sqrt{\frac{\log T}{t}}\right)=O\left(\sqrt{t\log T}\right)$$

为了完成分析，我们需要论证 “bad event” $bar\mathcal{E}$ 对悔值的贡献可以忽略不计：

$$\begin{array}{rl}\mathbb{E}\left[R(t)\right]& =\mathbb{E}\left[R(t)\mid \text{clean event}\right]\times \mathrm{Pr}\left[\text{clean event}\right]+\mathbb{E}\left[R(t)\mid \text{bad event}\right]\times \mathrm{Pr}\left[\text{bad event}\right]\\ & \le \mathbb{E}\left[R(t)\mid \text{clean event}\right]+t\times O\left(T^{-2}\right)\\ & \le O\left(\sqrt{t\log T}\right)\end{array}$$

定理2.8: 算法3在轮次 $t\le T$ 达到了悔值 $\mathbb{E}\left[R(t)\right]\le O\left(\sqrt{t\log T}\right)$

这种方法扩展到$K>2$的臂，如下所示：交替使用臂，直到某个手臂 $a$ 大概率比其他臂更糟糕。当这种情况发生时，丢弃所有这样的臂$a$并进入下一阶段。这种算法被称为连续消除（Successive Elimination）。

分析上述算法的性能。使$a^{\ast }$ 是一个最佳臂，它不能被停用。固定任意臂 $a$，使 $mu(a)<\mu (a^{\ast })$。考虑最后一轮 $t\le T$，当停用规则被调用时，臂 $a$ 仍然活跃。如同对 $K=2$ 个臂的论证，$a$ 和 $a^{\ast }$ 的置信区间必须在 $t$ 轮重叠。因此：

$$\begin{array}{rl}\Delta (a):=\mu (a^{\ast })-\mu (a)& \le 2(r_t(a^{\ast })+r_t(a))=4\cdot r_t(a)\end{array}$$

最后一个等式是因为 $n_t(a)=n_t(a^{\ast })$，因为算法一直在交替使用活跃的臂，而 $a$ 和 $a^{\ast }$ 在 $t$ 回合之前都是活跃的。$a$ 最多可以再玩一次：$n_T(a)\le 1+n_t(a)$。因此，我们有:
$$\begin{array}{r}\Delta (a)\le O(r_T(a))=O(\sqrt{\log (T)/n_T(a)})\text{for each arm a with μ(a)<μ(a∗)}\end{array}\text{\hspace{1em}(2.7)}$$

也就是说某个臂被选择了很多次就不会太差。

在 $t$ 轮中，手臂 $a$ 对悔值的贡献，可以表示为 $R(t;a)$ ，也可以表示为 $Delta(a)$ ，通过(2.7)，有：

$$R(t;a)=n_t(a)\cdot \Delta (a)\le n_t(a)\cdot O\left(\sqrt{\log (T)/n_t(a)}\right)=O\left(\sqrt{n_t(a)\log T}\right)$$

综合所有的臂，有：

$$\begin{array}{r}R(t)=\sum _{a\in \mathcal{A}}R(t;a)\le O\left(\sqrt{\log T}\sum _{a\in \mathcal{A}}\sqrt{n_t(a)}\right)\end{array}\text{\hspace{1em}(2.8)}$$

由于 $f(x)=\sqrt{x}$ 是一个实凹函数，并且 ${\sum }_{a\in \mathcal{A}}{n}_t(a)=t$ ，根据詹森不等式，我们有

$$\frac{1}{K}\sum _{a\in \mathcal{A}}\sqrt{n_t(a)}\le \sqrt{\frac{1}{K}\sum _{a\in \mathcal{A}}{n}_t(a)}=\sqrt{\frac{t}{K}}$$

将其带入(2.8)，可得到 $R(T)\le O(\sqrt{Kt\log T})$

定理：连续消除算法可以达到悔值：
$$\mathbb{E}\left[R(t)\right]=O\left(\sqrt{Kt\log T}\right)\text{for all rounds t≤T}\text{\hspace{1em}(2.9)}$$

观察(2.7)，$n_T(a)\le O\left(\log (T)/[\Delta (a){]}^2\right)$， 我们可以得到另一个悔值界:

$$R(T;a)=\Delta (a)\cdot n_T(a)\le \Delta (a)\cdot O\left(\frac{\log T}{[\Delta (a){]}^2}\right)=O\left(\frac{\log T}{\Delta (a)}\right)\text{\hspace{1em}(2.10)}$$

可以得到如下定理：

定理：连续消除算法可以达到悔值
$$\mathbb{E}[R(T)]\le O(\log T)\left(\sum _{\text{arms a with μ(a)<μ(a∗)}}\frac{1}{\mu (a^{\ast })-\mu (a)}\right)\text{\hspace{1em}(2.11)}$$

悔值界是 $T$ 的对数。

3.3 Optimism under uncertainty

让我们考虑另一种适应性探索的方法，即 $optimismunderuncertainty$：假设每个臂都是在迄今为止的观察下可能做到的最好，并根据这些乐观的估计选择最佳臂。这种算法的简单实现，称为UCB1。

一个臂 $a$ , 如果 $UC{B}_t(a)$ 较大，有两个原因（或其组合）：平均奖励 ${\bar{\mu }}_t(a)$很大，说明其奖励较高; 置信度 $r_t(a)$ 很大，在这种情况下，说明探索程度较低。 换句话说， $UC{B}_t(a)={\bar{\mu }}_t(a)+r_t(a)$ 中的两个总和分别代表利用和探索，将它们相加是解决探索-利用权衡的一种自然方式。

对于clean event。$a^{\ast }$ 是一个最优臂，$a_t$是算法在 $t$ 回合中选择的臂。根据该算法, $UC{B}_t(a_t)\ge UC{B}_t(a^{\ast })$ 。
在clean event下，$\mu (a_t)+r_t(a_t)\ge {\bar{\mu }}_t(a_t)$ 以及 $UC{B}_t(a^{\ast })\ge \mu (a^{\ast })$。于是有:
$$\begin{array}{r}\mu (a_t)+2r_t(a_t)\ge {\bar{\mu }}_t(a_t)+r_t(a_t)={\text{UCB}}_t(a_t)\ge {\text{UCB}}_t(a^{\ast })\ge \mu (a^{\ast })\end{array}\text{\hspace{1em}(2.12)}$$
因此:

$$\begin{array}{r}\Delta (a_t):=\mu (a^{\ast })-\mu (a_t)\le 2r_t(a_t)=2\sqrt{2\log (T)/n_t(a_t)}.\end{array}\text{\hspace{1em}(2.13)}$$

UCB1的悔值界与(2.9)和(2.11)一致。

四、初始化信息

关于平均奖励向量 $\mu$ 的一些信息可能事先为算法所知，并可用于提高性能。这种 “initial information” 通常包含 $\mu$ 的约束或其上的贝叶斯先验。

4.1 受约束的平均奖励

在一些固定的$d\in \mathbb{N}$中，典型的建模方法将臂嵌入到 ${\mathbb{R}}^d$ 中。因此，臂对应于${\mathbb{R}}^d$中的点，而 $\mu$ 是 ${\mathbb{R}}^d$（的子集） 上的一个函数，它将臂映射到它们各自的平均奖励。限制条件是 $\mu$ 属于某个 "well-behaved"的函数系列 $\mathcal{F}$ 。典型的假设是：

• 线性函数

  对于某些固定但未知的向量 $w\in {\mathbb{R}}^d$, $\mu (a)=w\cdot a$。

• 凹函数

  臂的集合为 ${\mathbb{R}}^d$ 中的凸子集，${\mu }^{\prime \prime }(\cdot )$ 存在且为负。

• Lipschitz函数

  对于所有的臂 $a,a^{\prime }$ 和固定常数 $L$ 有 $|\mu (a)-\mu (a^{\prime })|\le L\cdot \Vert a-a^{\prime }{\Vert }_2$ 。

这样的假设引入了臂之间的依赖关系，这样就可以通过观察其他臂的奖励来推断一个臂的平均奖励。特别地，Lipschitz性只允许"局部的"推论：只有观察到距离 $a$ 不太远的其他臂，才能了解关于臂a的信息。相比之下，线性和凹性允许"远程"推断：可以通过观察距离$a$ 很远的臂来了解臂$a$。

4.2 贝叶斯bandits

这里，$\mu$是从某个分布 $\mathbb{P}$ 中独立抽取的，称为 $\text{Bayesian prior}$(贝叶斯先验)。人们感兴趣的是 $\text{Bayesian regret}$： $\mathbb{P}$ 的期望值的悔值。这是贝叶斯方法的一个特例：模型的一个实例从一个已知的分布中取样，而性能是用这个分布的期望值来衡量的。

先验 $\mathbb{P}$ 隐含地定义了可行的平均奖励向量族 $\mathcal{F}$，此外还规定了 $\mathcal{F}$ 中的某些平均奖励向量是否以及在何种程度上比其他向量更有可能。

主要的缺点是采样假设在实践中可能非常理想化，而且算法可能不完全知道 "真实 "先验值。