每日练习之数学——砝码和天平

news2024/11/20 3:20:27

砝码和天平

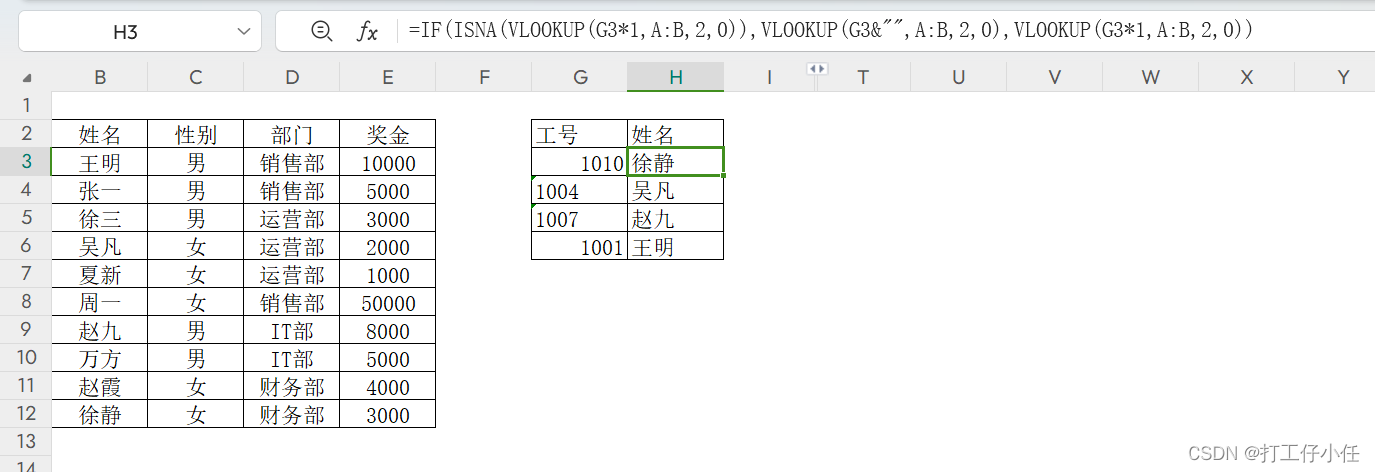
题目描述

运行代码

#include<iostream>
using namespace std;
int main()
{
	int w,m,T;
   cin>>T;
    while(T--)
    {
       cin>>w>>m;
        while(m)
        {
            if((m-1)%w==0)m=(m-1)/w;
            else if((m+1)%w==0)m=(m+1)/w;
            else if(m%w==0)m/=w;
            else break;
        }
        if(!m)
            cout<<"YES"<<endl;
        else 
            cout<<"NO"<<endl;
    }
}

代码思路

通过模拟天平的称量过程来检查是否能够使用给定的砝码（其质量为w的幂次）来表示一个特定的质量m。不是直接根据题目的数学思路来解决问题的，它实际上是在尝试模拟一个通过增加或减少少量质量来尝试使质量m能被w整除的过程。

首先读取测试数据的组数T。
对于每一组数据，读取w和m的值。
使用一个while循环尝试将m“调整”到一个可以被w整除的值。这里尝试了三种操作：
- 如果m-1可以被w整除，则将m设置为(m-1)/w。
- 如果m+1可以被w整除，则将m设置为(m+1)/w。
- 如果m本身可以被w整除，则将m除以w。
如果在循环结束后m变为0，那么输出"YES"，表示可以通过这些砝码来表示质量m（尽管这不是直接通过砝码组合，而是通过上述的“调整”过程）。
如果循环结束后m不为0，那么输出"NO"，表示无法通过这些砝码来表示质量m。

改进思路

问题

它没有直接利用到砝码是w的幂次这一特性。实际上，我们可以直接使用二进制表示法来判断m是否可以通过这些砝码来表示，而不需要这种“调整”过程。
它假设了通过增加或减少1个单位的质量可以使得m变得可以被w整除，这在实际情况下并不总是正确的。
即便m在某个点变得可以被w整除，这并不意味着它可以通过砝码组合来表示。因为代码没有检查这个整除后的m是否仍然在1到w的n次方减1的范围内。

改进

判断质量m是否可以用w的幂次砝码来表示，即判断m是否小于w的(n+1)次方（其中n是砝码的最大幂次，但在这个问题中我们不需要确切知道n，只需要知道w的(n+1)次方大于m即可）。

由于w可能非常大，直接计算w的(n+1)次方可能会导致整数溢出。但幸运的是，我们只需要检查m是否小于w的平方，因为任何大于w的m都可以通过w的更高次幂来表示（假设有足够的砝码）。

要判断一个质量m是否能用w的幂次砝码来表示，我们需要确保m可以表示为w的幂次的和，这相当于检查m的二进制表示是否只包含1（即m是w的幂次的组合）。但是，由于我们不知道具体的n（砝码的最大幂次），我们可以简单地检查m是否小于或等于w的某个足够大的幂次，比如w的32次方（因为int类型通常有32位）。

然而，更简单的方法是检查m是否小于w的(n+1)次方，其中n是使得w^(n+1)大于m的最小整数。由于w非常大，我们不能直接计算w^(n+1)，但我们可以知道，如果m小于w的平方，那么它肯定可以用w的幂次来表示（因为w^0到w^n的砝码可以覆盖从1到w^(n+1) - 1的所有整数）。