图论（二）-图的建立

news2024/11/20 6:29:55

引言： 建图，将图放进内存的方法

常用的建图方式：邻接矩阵，邻接链表，链式前向星

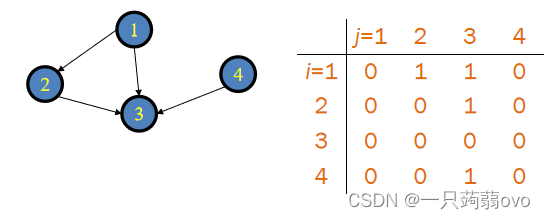
一、邻接矩阵

通过一个二维数组即可将图建立，邻接矩阵，考虑节点集合 $V=\left \{ 1,2,3......n \right \}$ ，用一个二维数组定义邻接矩阵 $A\left [ 1.....n \right ]\left [ 1.....n \right ]$ ，满足以下

对于一个简单的有向图（或无向图），邻接矩阵如下：

无向图：若 u 与 v 之间存在一条边，则 A[u][v]=A[v][u]=1 （两个方向）

有向图：若有一条 u 指向 v 的边，则 A[u][v]=1；若有一条 v 指向 u 的边，则 A[v][u]=1（单向）

邻接矩阵的空间消耗为 $O(V^{2})$ ，无向图的邻接矩阵为对称矩阵。在某些情况下，只存储邻接矩阵的对角线及以上的部分，这样，图占用的存储空间可以减少一半。

二、邻接链表（vector建表）

$Adj$ 为一个包含 V 条链表的数组，每个节点有一个链表，对于每个节点u∈V，邻接链表Adj[u]包含所有与节点u之间有边相连的节点v。

如果G是一个有向图，则对于边（u，v）而言，节点 v 将出现在链表 Adj [ u ]里，所有邻接链表的长度之和等于 E；如果G是一个无向图，对于边（ｕ，ｖ），节点ｖ将出现在链表 Adj [ u ] 里，节点 u 将出现在链表 Adj [ v ]里，所有邻接链表的长度之和为 2*E。

对一个有向图通过vector建图：

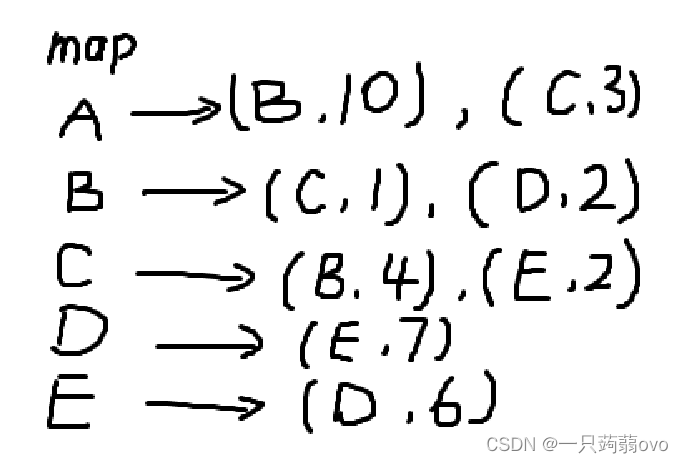
建图过程：

用结构体 node 存储两个数据（终点编号，边权值），建立 node 型的 vector 动态数组。建图也只需要将结构体直接插入 vector动态数组末端即可。


typedef struct Node{
    int v;  //终点编号
    int w;  //起点到终点的边权
}Node;
vector<Node> map[201];    //用 vector 建立（不是严格意义上的链表）
void get_map(int m)
{
    for(int i=1;i<=m;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        Node tmp;
        tmp.v=v;tmp.w=w;
        map[u].push_back(tmp);    //将 终点节点v 和 边权w 加入 节点u 的链表末尾
        tmp.v=u;tmp.w=w;    //如果为无向图，反向边
        map[v].push_back(tmp);   // 将 将终点节点u 和边权w 加入 节点v 的链表末尾
    }
}

邻接链表表示法的储存空间均为 O（V+E）

vector 数组建图的应用（使用）：

最小生成树prim算法（完整代码）：

#include<stdio.h>
#include<iostream>
#include<vector>
#include<queue>
#include<string.h>
#include<stdlib.h>
using namespace std;
struct node{
	int w;
	int v;
	friend bool operator<(node x,node y){ return x.w>y.w;} // 优先队列比较 按照w从小到大排？？ 
};
priority_queue<node>q; // 建立数据类型为node结构体的优先队列 
int n,m,dis[1001],vis[1001];
vector<node>map[1001]; // 以node结构体的 vector数组 
int sum=0;
void prim(int s)
{
	memset(dis,0x3f,sizeof(dis)); // 初始化 
	memset(vis,0,sizeof(vis));
	dis[s]=0;
	q.push((node){0,s});
	while(!q.empty())
	{
		int u=q.top().v;
		q.pop();
		if(vis[u]) continue;
		vis[u]=1;
		sum+=dis[u];
		for(int i=0;i<map[u].size();i++) // vector建图的使用 
		{
			int v=map[u][i].v;
			int w=map[u][i].w;
			if(dis[v]>w)
			{
				dis[v]=w;
				q.push((node){w,v});
			}
		}
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		node tmp; // vector 建图 
		tmp.v=v;tmp.w=w;
		map[u].push_back(tmp);
		tmp.v=u; map[v].push_back(tmp); // 反向边 
	}
	prim(1);
	for(int i=1;i<=n;i++) 
	{
		if(!vis[i]) 
		{
			printf("orz");
			return 0;
		}
	}
	printf("%d",sum);
	return 0; 
 }

三、链式前向星

链式前向星所用结构体和相关变量，建图函数

struct node{
	int to,next,w;
}edge[2001];
int head[1001];
int cnt=0;
void addedge(int u,int v,int w)
{
    edge[++cnt].to=v;
    edge[cnt].next=head[u];
	edge[cnt].w=w;
	head[u]=cnt;
}

初始化函数

//初始化函数
void init()
{
    memset(head,-1,sizeof(head));    //将head数组的值全置为-1.
    cnt=0;//初始化边的编号
}

对于一个有向图，用链式前向星建图：

关于结构体中 next 数组含义：某一条边的起点连接的上一个编号比它小的边。由于初始化，当某条边的next值为 -1 时，此条边为最后一条边。

运用链式前向星遍历图的过程：

首先根据节点 u 找到以 u 为起始点的边的编号，然后根据 next 找到下一条以 u 为起始点的边的编号，以此类推。

以链式前向星的方法建图的最小生成树prim算法：（主要代码）

void addedge(int u,int v,int w)
{
	edge[++cnt].v=v;
    edge[cnt].next=head[u];
	edge[cnt].w=w;
	head[u]=cnt;
}
void prim(int s)
{
	memset(dis,0x3f,sizeof(dis)); // 初始化 
	memset(vis,0,sizeof(vis));
	dis[s]=0;
	q.push((node1){0,s});
	while(!q.empty())
	{
		int u=q.top().v;
		q.pop();
		if(vis[u]) continue;
		vis[u]=1;
		sum+=dis[u];
		for(int i=head[u];i!=-1;i=edge[i].next)
		{
			int v=edge[i].v;
			int w=edge[i].w;
			if(dis[v]>w)
			{
				dis[v]=w;
				q.push((node1){w,v});
			}
		}
	}
}