数组-求和为k的连续子数组

news2024/10/6 2:24:12

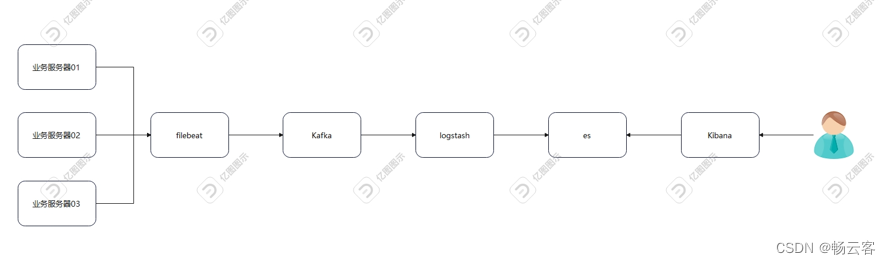
一、题目描述

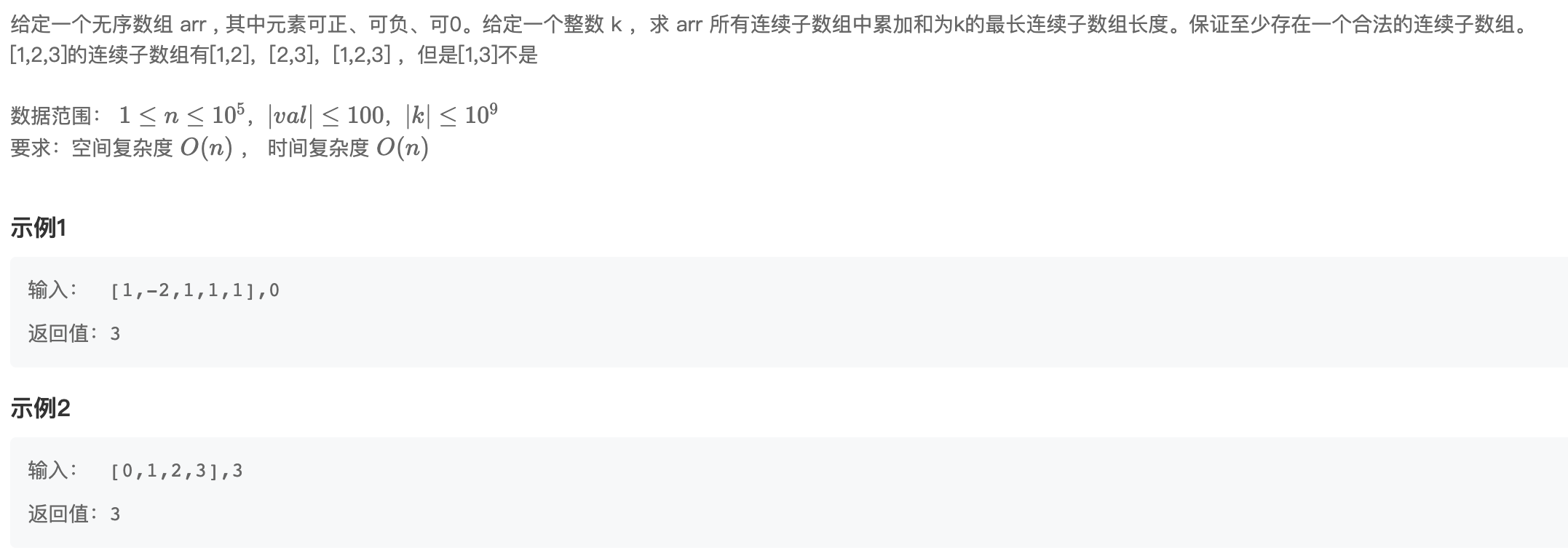
二、题目思路

这里注意：题目要求时间、空间复杂度都为O(n)，所以不能直接通过双层循环来暴力解(时间复杂度为O（n²）)，可以使用Map实现。

1. 遍历数组计算sum(i)，Map记录sum值第一次出现的位置：

[<sum(0),index0>,<sum(1),index1>,<sum(2),index2>,<sum(3),index3>...]

这里Map初始化后要加上<0,-1>，表示包含没有元素时的sum情况。

这里举个例子看一下为什么要初始化加<0,-1>

假设测试用例为：arr=[0,1,2,3],k=3

(1)如果不加，执行过程：

<sum=0,i=0>	<sum=1,i=1>	<sum=3,i=2>	<sum=6,i=3>
sum-k=-3	sum-k=-2	sum-k=0	sum-k=3
diff=?	diff=?	diff=2	diff=1

(2)如果加，执行过程：

<sum=0,i=-1>	<sum=1,i=1>	<sum=3,i=2>	<sum=6,i=3>
sum-k=-3	sum-k=-2	sum-k=0	sum-k=3
diff=?	diff=?	diff=3	diff=1

可见加上是合理的，因为当满足sum=k，sum-k=0，就应该包含第一个元素。

2.当计算到sum(j)时，发现[diff=sum(j)-k]在Map中出现过，此时j-Map.get(diff)和已经记录的len作比较，len取较大值更新

三、代码实现

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * max length of the subarray sum = k
     * @param arr int整型一维数组 the array
     * @param k int整型 target
     * @return int整型
     */
    public int maxlenEqualK (int[] arr, int k) {
        // write code here
        //使用Map记录最先出现的(sum,index)作为键值对
        Map<Integer,Integer> sumIndex=new HashMap<>();

        sumIndex.put(0,-1);
        //初始化Map，什么都不加的时候sum=0
        int sum=0;
        int len=0;
        //遍历数组计算sum(i)，Map记录sum值第一次出现的位置：
        //[<sum(0),index0>,<sum(1),index1>,<sum(2),index2>,<sum(3),index3>...]
        //当计算到sum(j)时，发现[diff=sum(j)-k]在Map中出现过
        //此时j-Map.get(diff)和已经记录的len作比较，len取较大值更新
        for(int i=0;i<arr.length;i++){
            //计算sum值
            sum+=arr[i];
            //记录第一次出现sum的位置
            if(!sumIndex.containsKey(sum)){
                sumIndex.put(sum,i);
            }
            //查看是否有满足条件的sum
            if(sumIndex.containsKey(sum-k)){
                int nowlen=i-sumIndex.get(sum-k);
                //更新最大len
                len=len<nowlen?nowlen:len;
            }
        }

        return len;
    }
}