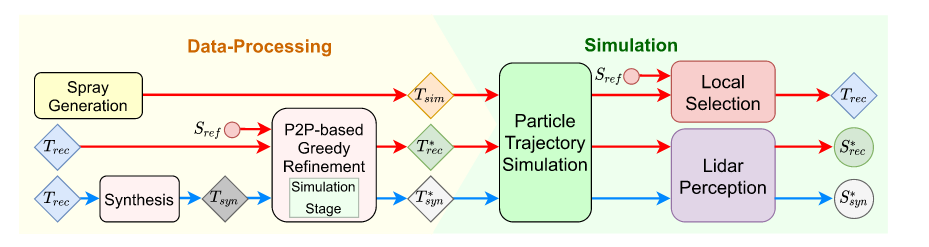
文章目录
- 遗传算法
- 一、介绍
- 二、遗传算法的思想
- 1.试用范围
- 2.案例
- 2.1 算法思路
- 2.2 代码实现
遗传算法
一、介绍
遗传算法是一个启发式算法,主要可以用于优化问题,下边将进行举例来进行初步了解。
举例:
-
从做菜说起,首先你是一个大厨,想创作出一些美味,刚开始会随机生成很多个原始配方每种配方所用的原料和手法都不相同,有无穷多种解,传统算法难以求解。
-
接下来会请一些评委对这些配方做出的菜进行打分(适应度)
-
分数高的配方会进行配方交叉会保留一部分评分高的配方,舍弃评分低的配方。配方交叉后会产生新的配方。
-
有时候会再交叉后会变更食材或者烹饪方式(变异)也就是进行大胆尝试创新。
变异可能会带来惊喜,也有可能有惊无喜,所以只小概率进行 -
继续对新的配方进行评分,继续交叉,小概率变异,不断循环一直到无改进空间为止。
二、遗传算法的思想

1.试用范围
(1)线性/非线性、多目标、多函数优化类问题。
(2)不依赖于问题的背景和领域,连续/离散、单峰/多峰形式均可以
(3)和模拟退火相比有良好的全局搜索能力,不易陷入局部最优。
(4)相比于粒子群算法,遗传算法可以直接求离散问题。
注:
1. 离散优化问题常见的有组合优化、整数规划等。离散优化决策变量是有限集合中的元素,例如,在组合优化问题中,可能需要选择一组物品的组合,其中每个物品的选择是二进制的(选或不选)。
2. 连续优化决策变量可以是实数范围内的任意值(或者说在一个区间内),没有跳跃或离散点。例如,在求解一个函数的最小值时,x 可以是实数域内的任何值。
3.求解方法:
连续优化:通常使用基于梯度的优化算法(如梯度下降、牛顿法、拟牛顿法等)或全局优化算法(如粒子群优化、遗传算法等)。
离散优化:可能使用基于枚举的算法(如回溯法、分支限界法等)、整数规划方法(如分支定界法、割平面法等)、元启发式算法(如离散粒子群优化、遗传算法等)或特定的组合优化算法(如贪心算法、动态规划等)。
2.案例
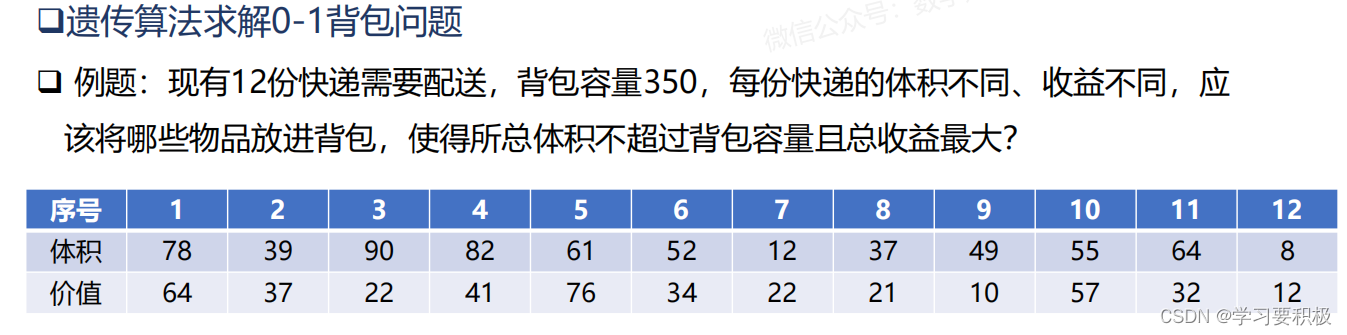
很明显这是一个离散问题(组合问题)。
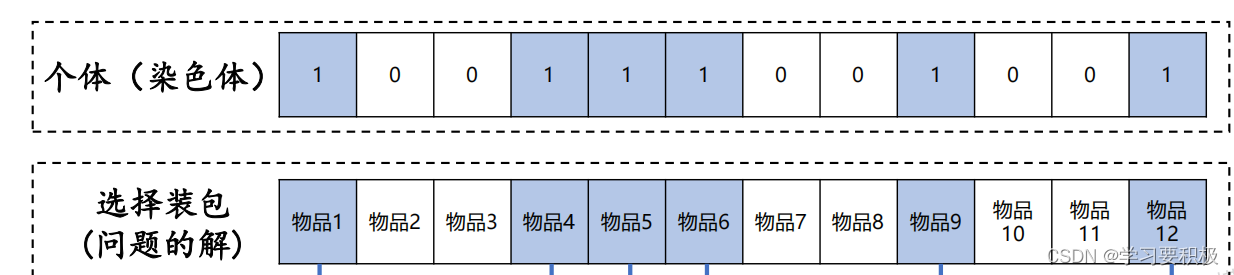
1.我们采用0和1来表示物品是否装进包内。
2.每一个物品的装包状态看成一个基因
3.问题的一个解是12位的数字所组成的个体。
2.1 算法思路
种群初始化->选择运算->交叉运算->变异运算->迭代循环。
选择运算:
主要是从每一代群体中挑选出优良个体遗传给下一代。
准则:
1. 适应度越高的个体被选中的几率越大。
2. 适应度较低的个体仍有被选中的可能。
问题: 为什么不直接从大到小排序选择前几个适应度比较高的个体?:
1.适应度最高的几个个体意味着适应度相差无几。
2.往往基因也很相似。
3.如果每次只选择适应度最高的个体就意味着每轮所选择的个体相似度很高。
4.也就意味着他们的后代的相似度也高,进化陷入了停滞,意味着陷入局部最优解。
我们采用轮盘赌法(思想见代码)
2.2 代码实现
%设置迭代次数
maxg=180;
%设置交叉概率
p1=0.8;
%设置变异概率
p2=0.03;
%体积和价值
C = [78,39,90,82,61,52,12,37,49,55,64,8]; % 物品体积
W = [64,37,22,41,76,34,22,21,10,57,32,12]; % 物品价值
%惩罚系数
alpha=50;
%基因数目
N=12;
Vlim=350;
maxItem=80;
%初始化种群,80个
population=randi([0,1],80,N);
%开始迭代
for i=1:maxg
%适应度计算
for j=1:maxItem
fit(j)=fitness(C,W,alpha,population(j,:),Vlim);
end
%适应度的最大值
maxfit=max(fit);
%最大值的索引,有可能多个
maxIndex=find(fit==maxfit);
%记录下初始最优的个体
bestItem=population(maxIndex(1,1),:);
%采用轮盘赌法根据适应度进行初步筛选优秀个体
%每个个体被选中的概率
selectP=fit./sum(fit);
%累计概率
selectP=cumsum(selectP);
%比较数组bet
bet=rand(maxItem,1);
bet=sort(bet);
%更新bet
bet_i=1;
%更新个体
item_i=1;
%开始找,直到选出与种群数量相等的个体数
while bet_i<=maxItem
if selectP(item_i)>bet(bet_i)
choosef(bet_i,:)=population(item_i,:);
bet_i=bet_i+1;
else
item_i=item_i+1;
end
end
%交叉,两两
for i=1:2:maxItem
p_v=rand;
if p_v<p1 %80概率交叉
%每个基因还有一半概率交叉
q=randi([0,1],1,N);
for j=1:N
if q(j)==1
temp=choosef(i+1,j); % 第i+1个个体的第j个基因赋值给临时变量
choosef(i+1,j)=choosef(i,j);
choosef(i,j)=temp;
end
end
end
end
%变异
for n=1:maxItem
for m=1:N
variation=rand(1,1);
if variation<p2 %有2%的概率进行变异
choosef(n,m)=~choosef(n,m);%基因取反
end
end
end
population=choosef;
population(1,:)=bestItem;
%本轮的最优适应度
bestfit(i)=maxfit;
end
figure
plot(bestfit)
xlabel('迭代次数')
ylabel('目标函数值')
title('遗传算法适应度迭代')
%适应度函数
function result=fitness(c,w,alpha,item,vlim)
%总体积
totalC=sum(item.*c);
%总价值
totalV=sum(item.*w);
if totalC>vlim
%让超过约束的方案适应度很低,也就是几乎不选择。
totalV=totalV-alpha*(totalV-vlim);
end
result=totalV;
end
适应度图: