Dijkstra —— 单源最短路

讲解

时间复杂度

• 朴素 Dijkstra：$O(n^2)$ ，$n$ 是顶点数。
• 堆优化 Dijkstra：$O(mlogn)$ ，$m$ 是边数，$n$ 是顶点数。

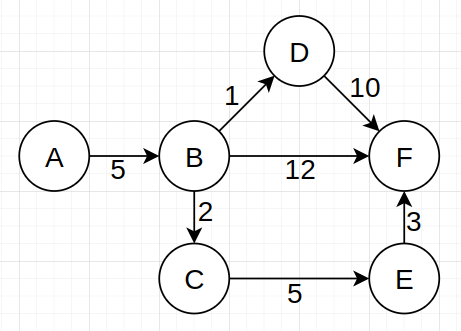
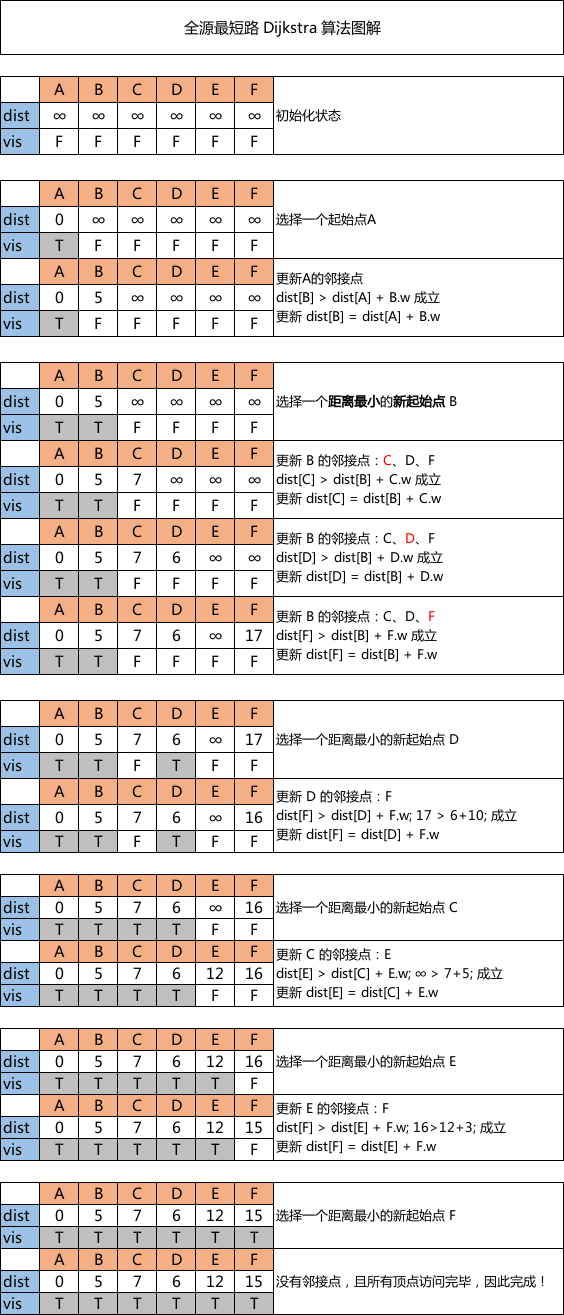
核心思想：具体看图解，文字和图我感觉都挺详细的。

适用场景：

• 朴素 Dijkstra：稠密图
• 堆优化 Dijkstra：稀疏图

图解

Java

朴素

static final int MAX = 1000;
static final int INF = 0xffffff; // 无穷大
static int[][] edge = new int[MAX][MAX]; // 邻接矩阵
static int[] dis = new int[MAX]; // 记录从起点到各个点的最短路径
static boolean[] vis = new boolean[MAX]; // 标记
static int n, m, s; // 顶点数、边数

public static void dijkstra(int s) {
    Arrays.fill(dis, INF);
    dis[s] = 0;
    for(int i = 1; i <= n; i++) { // 保证每个顶点都会被访问
        int u = 0;
        // 从未使用过的顶点中选一个距离起点的最短路径
        for(int v = 1; v <= n; v++) {
            if(!vis[v] && dis[u] > dis[v]) u = v;
        }
        vis[u] = true;
        // 更新 u 所有邻接点的路径
        for(int v = 1; v <= n; v++) {
            // 当前结点 u 的距离（起点到 u 的距离） + 结点 u 的邻接点 v < 结点 v 的距离，则更新
            dis[v] = Math.min(dis[v], edge[u][v] + dis[u]);
        }
    }
}

使用堆优化

import java.util.*;

public class Main {
    static final int MAX = 150005;
    static final int INF = 0x7ffffff;
    static ArrayList<Edge>[] G = new ArrayList[MAX];
    static int[] dis = new int[MAX];
    static boolean[] vis = new boolean[MAX];
    static int n, m;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt(); m = sc.nextInt();
        for(int i = 1; i <= n; i++) G[i] = new ArrayList<>();
        while(m-- != 0) {
            int u = sc.nextInt(), v = sc.nextInt(), w = sc.nextInt();
            G[u].add(new Edge(v, w));
        }
        dijkstra(1);
        System.out.println(dis[n] == INF ? -1 : dis[n]);
    }

    public static void dijkstra(int s) {
        PriorityQueue<Edge> queue = new PriorityQueue<>();
        Arrays.fill(dis, INF);
        queue.add(new Edge(s, 0));
        dis[s] = 0;
        while(!queue.isEmpty()) {
            int u = queue.poll().to; // 距离最短的点
            if(vis[u]) continue;
            vis[u] = true;
            for(int i = 0; i < G[u].size(); i++) { // 更新邻接点
                Edge v = G[u].get(i);
                if(dis[v.to] > dis[u] + v.w) {
                    dis[v.to] = dis[u] + v.w;
                    queue.add(new Edge(v.to, dis[v.to]));
                }
            }
        }
    }

}

class Edge implements Comparable<Edge> {
    int to, w;
    public Edge(int to, int w) {
        this.to = to;
        this.w = w;
    }

    @Override
    public int compareTo(Edge o) {
        return this.w - o.w;
    }
}

C++

朴素

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 510;
const int INF = 0x3f3f3f3f;

int G[N][N];
int dist[N];
bool vis[N];

int n, m;

void dijkstra(int s) {
    memset(dist, INF, sizeof(dist));
    dist[s] = 0;
    for(int i = 1; i <= n; i++) {
        int u = 0;
        for(int v = 1; v <= n; v++) {
            if(!vis[v] && dist[u] >  dist[v]) u = v;
        }
        vis[u] = true;
        for(int v = 1; v <= n; v++) {
            dist[v] = min(dist[v], G[u][v] + dist[u]);
        }
    }
}

int main() {
    cin >> n >> m;
    memset(G, INF, sizeof(G));
    while(m--) {
        int u, v, w;
        cin >> u >> v >> w;
        G[u][v] = min(G[u][v], w);
    }
    dijkstra(1);
    if(dist[n] == INF) cout << -1 << endl;
    else cout << dist[n] << endl;
    return 0;
}

使用堆优化

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>

using namespace std;

const int N = 150005;
const int INF = 0x3f3f3f3f;

typedef pair<int, int> PII;

struct edge {
    int w;
    int to;
    int next; // 下一条边的编号
} edge[N];

int head[N];
int idx;
int dist[N];
bool vis[N];
int n, m;

void add(int u, int v, int w) {
    idx++;
    edge[idx].w = w;
    edge[idx].to = v;
    edge[idx].next = head[u];
    head[u] = idx;
}

void dijkstra(int s) {
    memset(dist, INF, sizeof(dist));
    dist[s] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, s});
    while(heap.size()) {
        PII t = heap.top();
        heap.pop();
        int u = t.second;
        if(vis[u]) continue;
        vis[u] = true;
        for(int v = head[u]; v != -1; v = edge[v].next) {
            struct edge e = edge[v];
            if(dist[e.to] > dist[u] + e.w) {
                dist[e.to] = dist[u] + e.w;
                heap.push({dist[e.to], e.to});
            }
        }
    }
}

int main() {
    memset(head, -1, sizeof(head));
    cin >> n >> m;
    while(m--) {
        int u, v, w;
        cin >> u >> v >> w;
        add(u, v, w);
    }
    dijkstra(1);
    if(dist[n] == INF) cout << -1 << endl;
    else cout << dist[n] << endl;
    return 0;
}

Floyd —— 多源最短路

讲解

时间复杂度：$O(n^3)$ ，$n$ 是顶点数。

核心思想：以 i 为起点，j 为终点，i 到 j 的距离是否可以通过一个中转点 k 从而缩短距离。

Tips：j 不一定是 i 的邻接点。

上图解释，从 A 点到 B 点，可以通过一个中转点 C 从而缩短距离。

适用场景：稠密图。

Java

public class Floyd {
    static final int INF = 0x7ffffff; 
    static final int MAX = 1010;
    static int[][] G = new int[MAX][MAX];
    static int n;

    public static void init() {
        for(int i = 1; i <= n; i++) {
            Arrays.fill(G[i], INF);
            G[i][i] = 0;
        }
    }

    public static void floyd() {
        for(int k = 1; k <= n; k++) { // 中转点
            for (int i = 1; i <= n; i++) { // 起点
                // 对于每个顶点 k 和任意顶点对 (i,j) i != j, k != i, k !=j
                // 若 G[i][j] > G[i][k] + G[k][j] 则将 G[i][j] 修改为 G[i][k] + G[k][j] 的值
                // 【记录路径可忽略】并且将 Path[i][j] 修改为 k（此步用于记录从某个顶点到某个顶点需要结果 k 顶点）
                if(i == k || G[i][k] == INF) continue;
                for (int j = 1; j <= n; j++) { // 终点
                    G[i][j] = Math.min(G[i][j], G[i][k] + G[k][j]);
                }
            }
        }
    }
}

C++

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 500;
const int INF = 0x3f3f3f3f;

int G[N][N];
int n, m, k;

void floyd() {
    for(int k = 1; k <= n; k++) {
        for(int i = 1; i <= n; i++) {
            if(i == k || G[i][k] == INF) continue;
            for(int j = 1; j <= n; j++) {
                G[i][j] = min(G[i][j], G[i][k] + G[k][j]);
            }
        }
    }
}