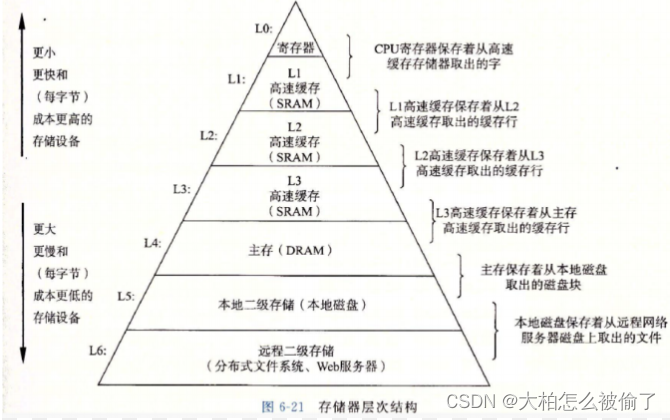
同一个点的坐标在不同基坐标系中转换
设 (O, i,j,k)坐标系中点P坐标为
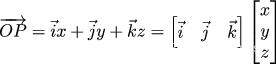
假设基坐标(i,j,k)与(i’,j’,k’)的转换关系为
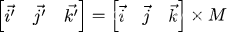
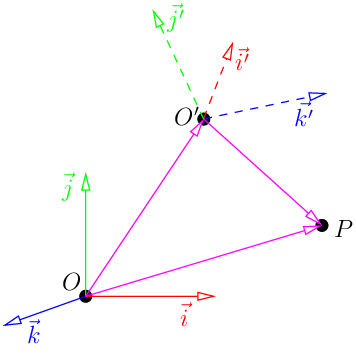
如图,可以看出
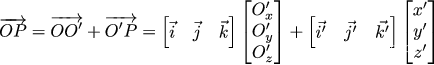
其中(x’,y’,z’)为点P在基坐标(i’,j’,k’)下的坐标,(Ox’,Oy’,Oz’)为(i’,j’,k’)坐标系原点O’在(i,j,k)坐标系中的位置
将基坐标(i’,j’,k’)转换(i,j,k)公式代入,并提出(i,j,k)

左右的看作在(i,j,k)坐标系下的表示,可得
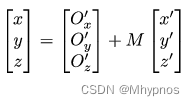
推出(x’,y’,z’)在(i,j,k)坐标系中的位置变换公式
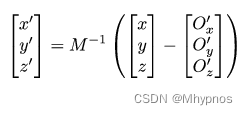
前一节的投影矩阵,摄像机是与世界空间的坐标系平行,以世界坐标的零点为观察点求得公式
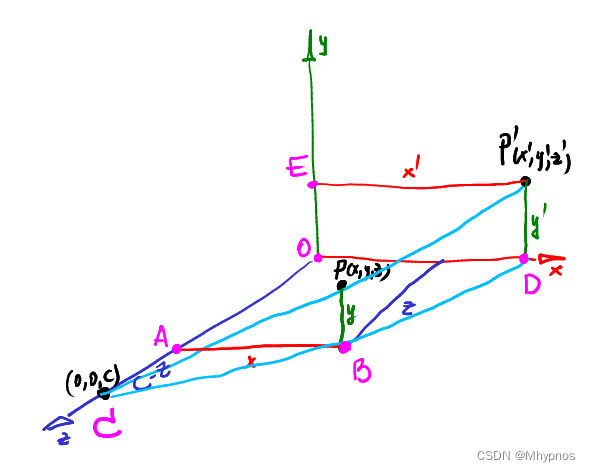
因此要求出模型在世界空间中得坐标,如何转换到新得观察点target,并且和摄像机基坐标平行的坐标系中。
首先,有相机的位置cameraPos,相机看向的某个原点target,相机向上的朝向up,求出相机的基坐标
Vec3f z = (cameraPos - target).normalize();
Vec3f x = (up ^ z).normalize();
Vec3f y = (z ^ x).normalize();
根据前面公式,(Ox’,Oy’,Oz’)即为观察点的坐标
Matrix t = Matrix::identity(4);
t[0][3] = -target.x;
t[1][3] = -target.y;
t[2][3] = -target.z;
再求出M的逆变换,世界坐标的基坐标就是单位矩阵,所以M就是摄像机空间的基坐标构成的矩阵
矩阵的列向量通常被视为基向量,所以M为
Matrix t1 = Matrix::identity(4);
for (int i = 1; i < 3; i++) {
t1[i][0] = x[i];
t1[i][1] = y[i];
t1[i][2] = z[i];
}
则世界坐标到摄像机空间坐标的变换矩阵为
t1.inverse() * t
M矩阵是正交矩阵(每列视作向量时两两垂直,切长度为1,行列相等)
把正交的向量,按列向量的形式放进一个花括号内,即组成了一个正交向量组
基向量是构成向量空间的一个向量组(坐标系),若基向量组内的向量两两正交,且向量长度均为1,则称作:标准正交基。
又因为正交矩阵的逆等于转置
所以
for (int i = 0; i < 3; i++) {
t1[0][i] = x[i];
t1[1][i] = y[i];
t1[2][i] = z[i];
}
return t1 * t;
投影矩阵的c为-1/z,z为摄像机到观察点的距离
projection[3][2] = -1.f / (camera - target).norm();

Gouraud shading根据三角形三个顶点的法线求着色,再对三角形内部点插值
auto I1 = normalcoords[0] * light_dir;
auto I2 = normalcoords[1] * light_dir;
auto I3 = normalcoords[2] * light_dir;
//...
auto c = TGAColor(255, 255, 255) * I1 * alpha + TGAColor(255, 255, 255) * I2 * beta + TGAColor(255, 255, 255) * I3 * gamma;
image.set(x, y, c);

项目跟随练习代码地址