广度优先搜索

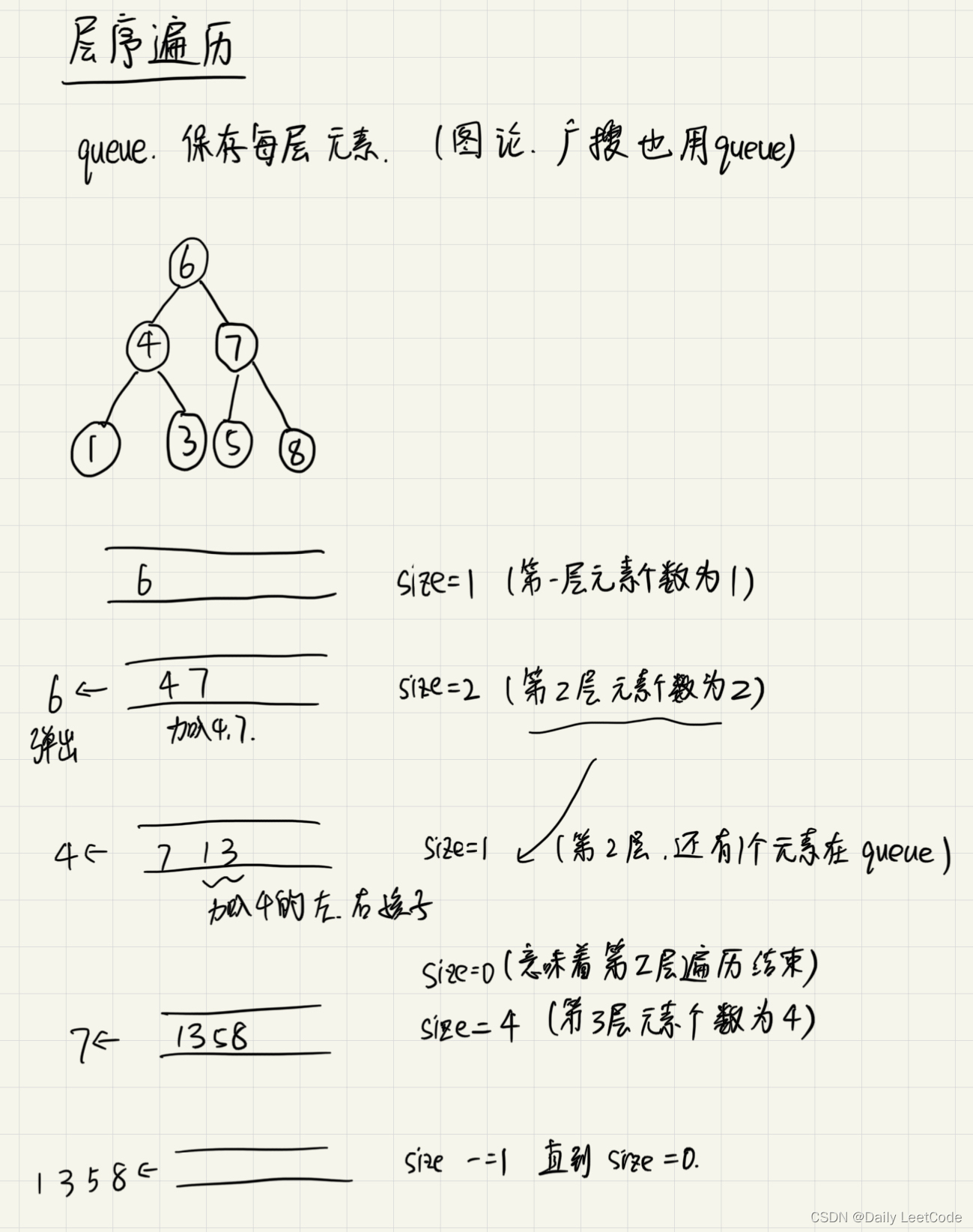
总结一下，思路就是：

加入元素，记录size，size就是当前这一层的元素个数。不断弹出元素，size -= 1， 同时加入弹出元素的左右孩子，直到size==0，说明当前层已经完全遍历完，然后让size=queue里面的元素个数，就是下一层一共有多少个元素，重复上述步骤。直到size==0且queue中没有元素了，就遍历完成了。

队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

LeetCode对应的题（都是同样的思路）：

102.二叉树的层序遍历
107.二叉树的层次遍历II
199.二叉树的右视图
637.二叉树的层平均值
429.N叉树的层序遍历
515.在每个树行中找最大值
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针II
104.二叉树的最大深度
111.二叉树的最小深度

102. 二叉树的层序遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        que = collections.deque([root])
        result = []
        while que:
            level = []
            for i in range(len(que)):
                cur = que.popleft()
                level.append(cur.val)
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
            result.append(level)
        return result

107.  二叉树层序遍历（按照从下层到上层的顺序输出）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        que = collections.deque([root])
        result = []
        while que:
            level = []
            for i in range(len(que)):
                cur = que.popleft()
                level.append(cur.val)
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
            result.append(level)
        return result[::-1]