目录

一、求所有结点个数

1.1 递归思路

1.2 递归分支图

1.3 递归栈帧图

1.4 C语言实现

二、求叶子结点个数

2.1 递归思路

2.2 递归分支图

2.3 递归栈帧图

2.4 C语言实现

三、求第K层的结点个数

3.1 递归思路

3.2 递归分支图

3.3 递归栈帧图

3.4 C语言实现

四、求二叉树高度

4.1 递归思路

4.2 递归分支图

4.3 递归栈帧图

4.4 注意事项

4.5 C语言实现

---

一、求所有结点个数

1.1 递归思路

考虑特殊情况：

1. 如果是空节点，返回0

考虑一般情况：

1. 总结点的数目就是左右子树所含结点的和加上自身结点

2. 每个节点都可被看作根节点，去重复递归左右子树

1.2 递归分支图

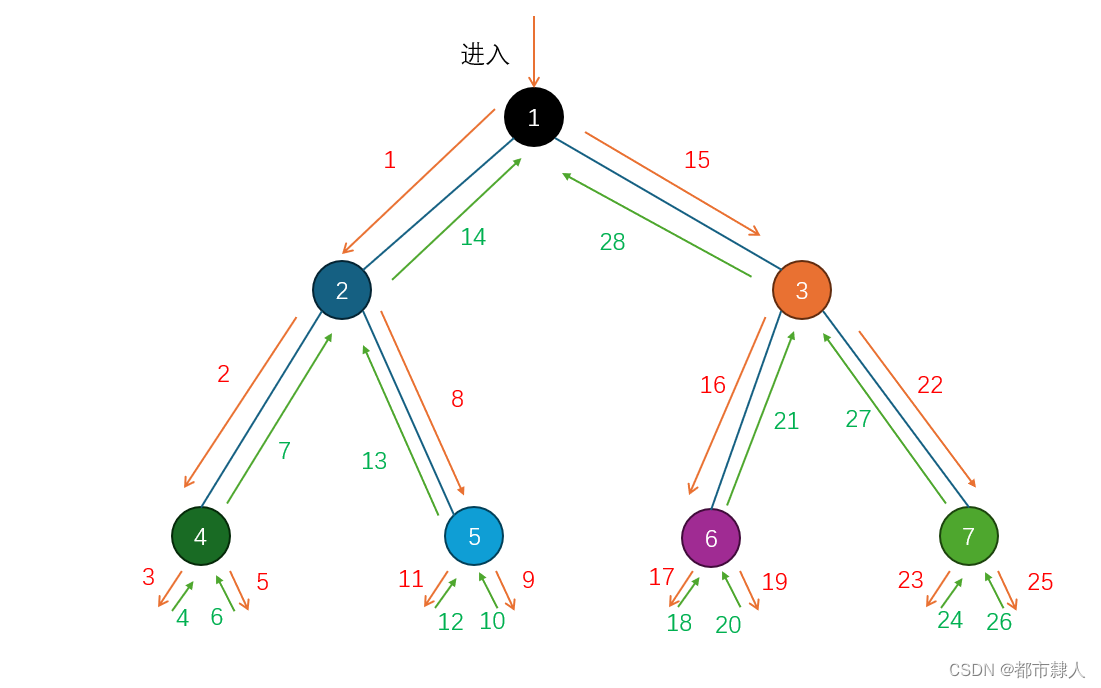
1.3 递归栈帧图

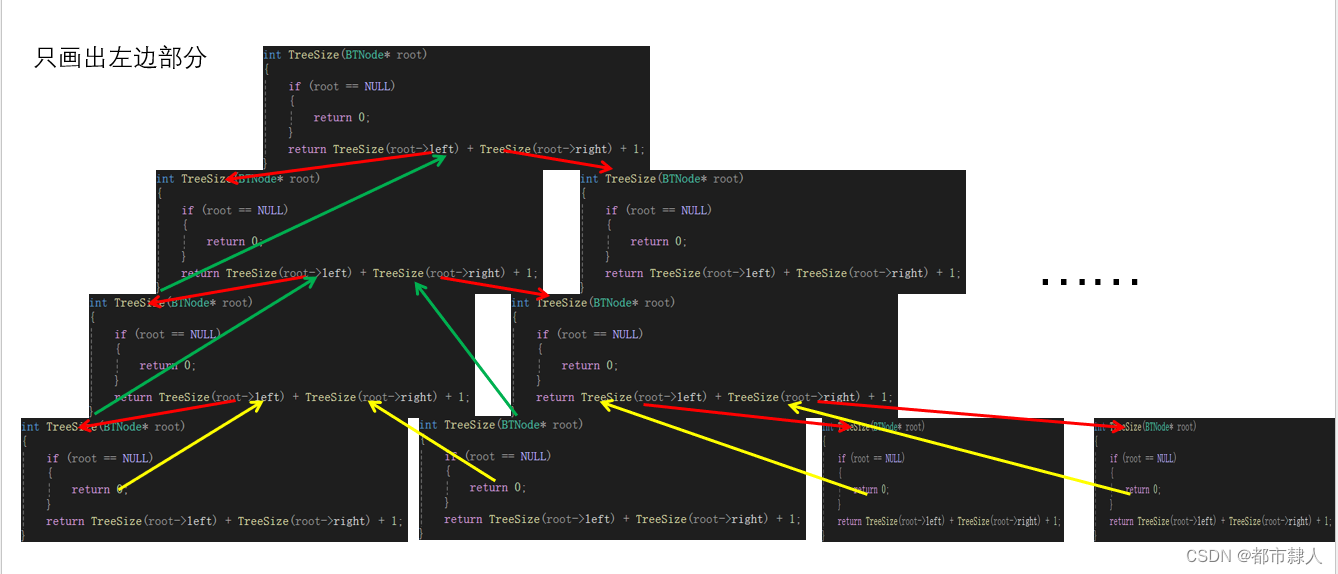
1.4 C语言实现

int TreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

二、求叶子结点个数

2.1 递归思路

考虑特殊情况：

1. 如果是空节点，则返回0
2. 如果是叶子结点，则返回1

考虑一般情况：

1. 总结点的数目就是左右子树所含结点的和

2. 每个节点都可被看作根节点，去重复递归左右子树

2.2 递归分支图

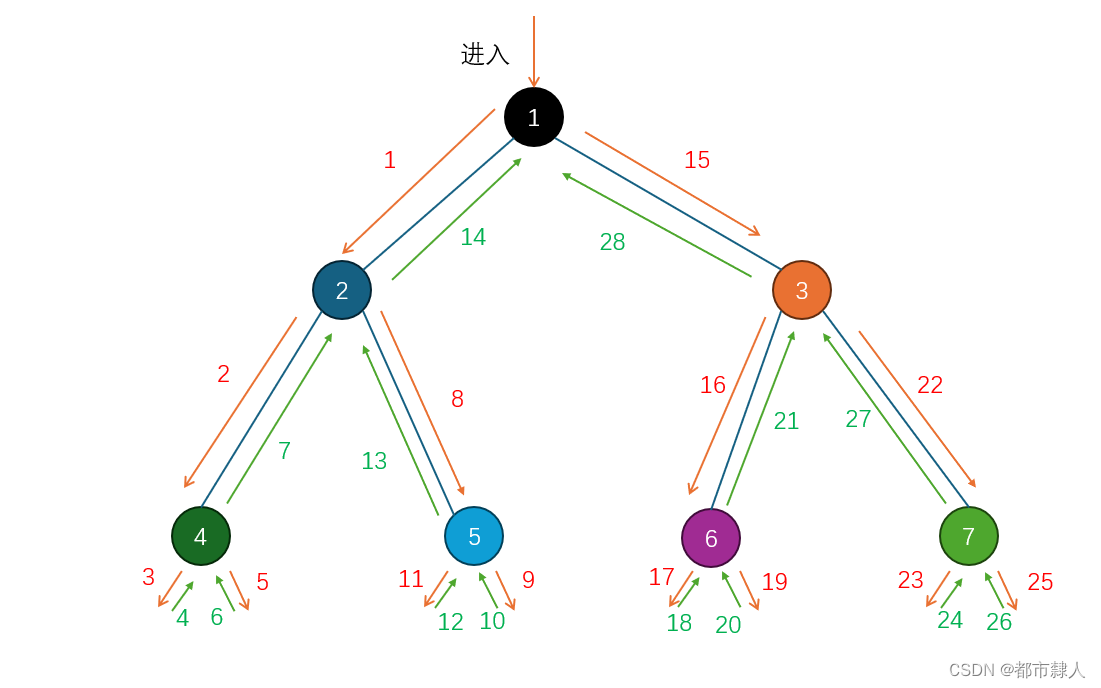
2.3 递归栈帧图

 

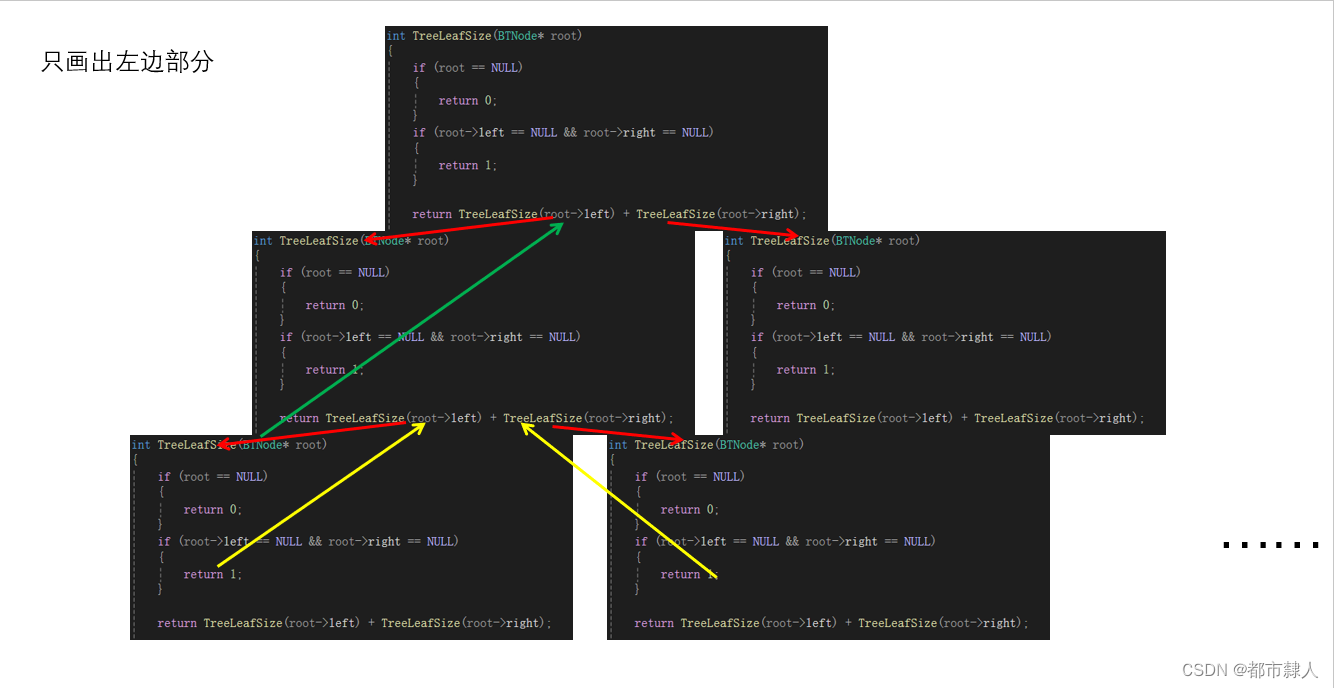
2.4 C语言实现

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return TreeLeafSize(root->left) + TreeLeafSize(root->right);

}

三、求第K层的结点个数

3.1 递归思路

考虑特殊情况：

1. 如果结点为空，返回0
2. 如果层数为1，返回1

考虑一般情况：

每个节点都可被看作根节点，去重复递归左右子树。那么此时层数要减去1

3.2 递归分支图

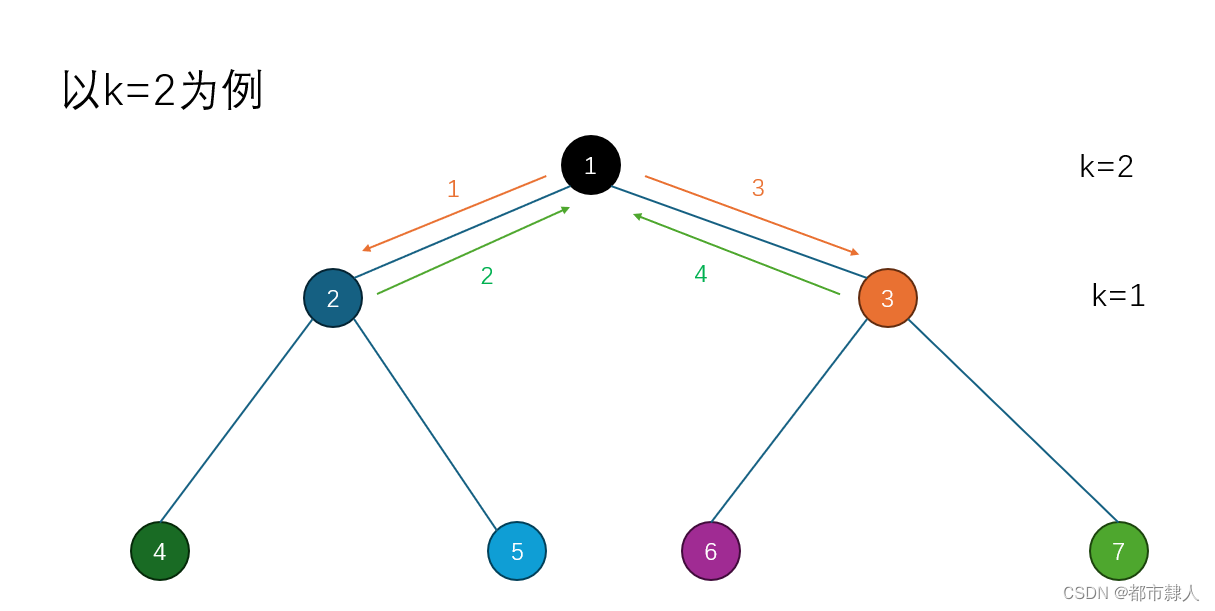
3.3 递归栈帧图

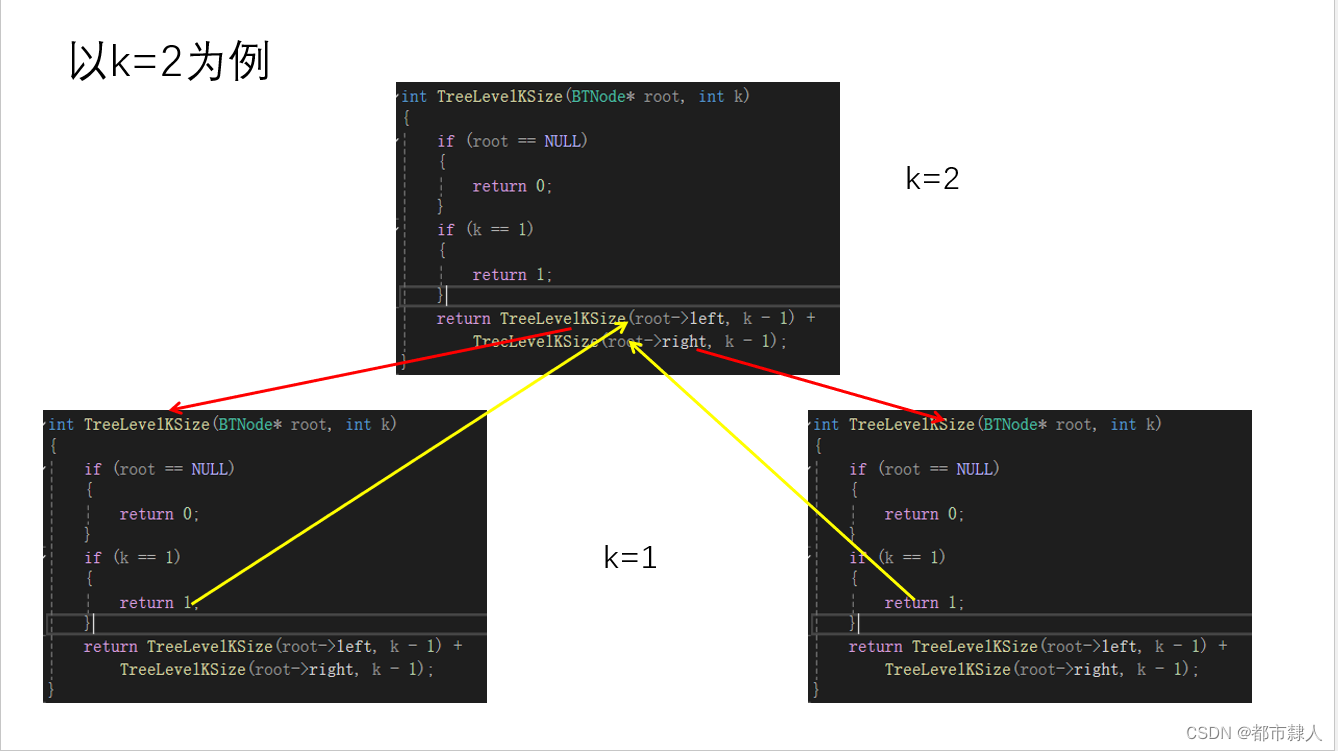
3.4 C语言实现

int TreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

四、求二叉树高度

4.1 递归思路

考虑特殊情况：

1. 如果结点为空，返回0

考虑一般情况：

1. 高度就等于子树的高度加上自身的高度
2. 返回的是左右子树中更大的值

4.2 递归分支图

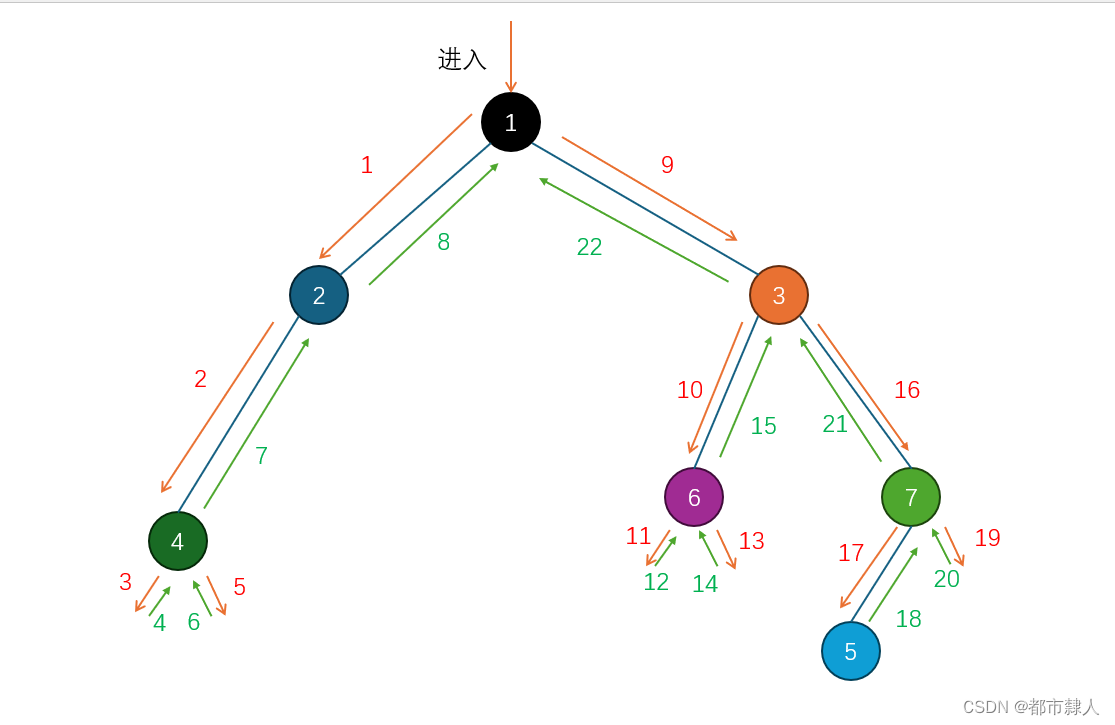
4.3 递归栈帧图

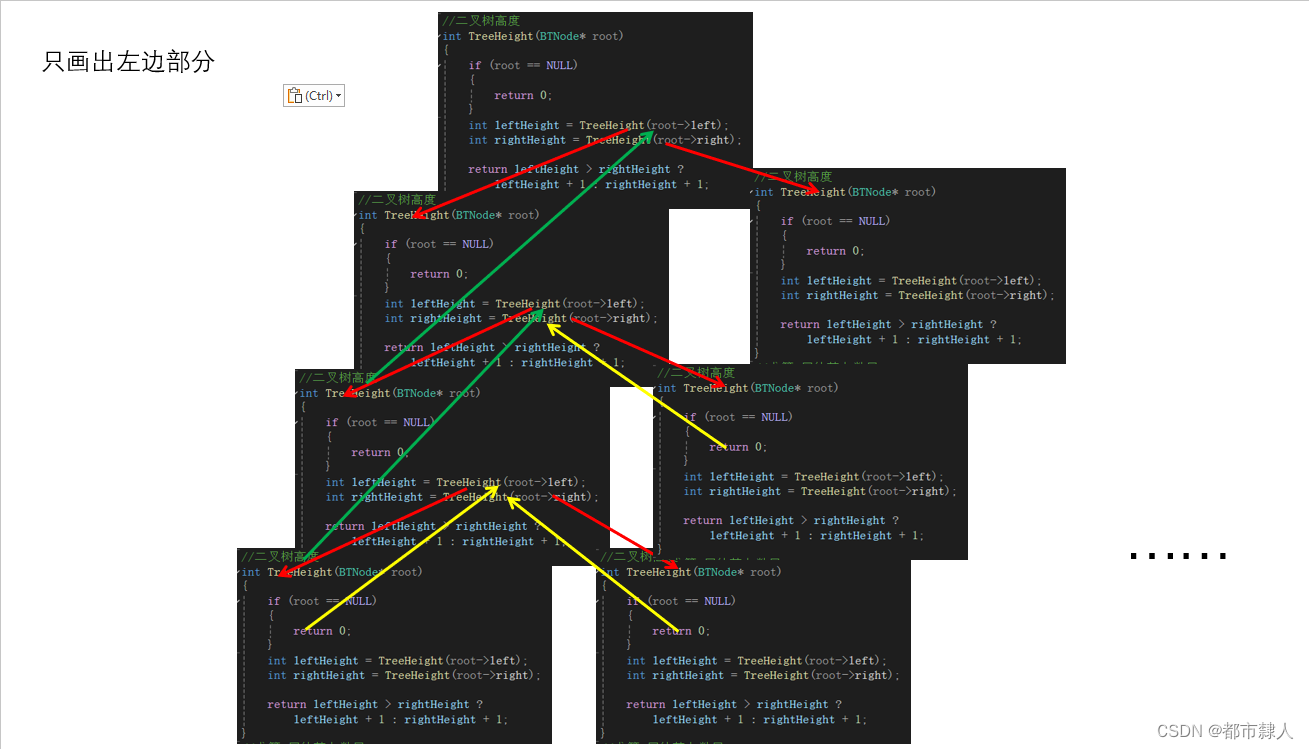
4.4 注意事项

由递归的知识可知，函数每次调用都会建立栈帧，各个栈帧间互不影响，所以需要把每次得到的值存起来，不然每次调用都会去再次递归寻找。大大浪费时间，降低程序执行的效率。

4.5 C语言实现

int TreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight ?
		leftHeight + 1 : rightHeight + 1;
}