红黑树底层封装map、set C++

news2024/12/24 9:17:25

目录

一、框架思考

三个问题

问题1的解决

问题2的解决：

问题3的解决：

二、泛型编程

1、仿函数的泛型编程

2、迭代器的泛型编程

3、typename：

4、++/--重载

三、原码

红黑树

map

set

一、框架思考

map和set都是使用红黑树底层，要怎么实现同一个底层，但是实现不同的功能呢？

三个问题


1、map是pair模型，而set是key模型

2、map和set的迭代器用法是一样的，如何实现？

3、插入时，set和map插入的类型不同，如何实现？

我们是一个简单的实现，而不是全部，所以抓重点，化繁为简
只关注和当前我么要实现功能有关系的部分，其他的统统不关注

问题1的解决


RBTree的节点传的是一个模板

template<class T>
struct BRTreeNode
{
	BRTreeNode<T>* _parent;
	BRTreeNode<T>* _right;
	BRTreeNode<T>* _left;
	T _data;
	Colour _col;

	BRTreeNode(const T& data)
		:_parent(nullptr)
		, _right(nullptr)
		, _left(nullptr)
		, _data(data)
		, _col(RED)
	{
	}

};

map传<K,pair<K,V>>
set传<K,K>

我set要用的是key模型的BRTree，所以传的是<K，K>
我map要的是key-value模型的BRTree，所以传的是<K，pair<K,V>>
对应的BRTree传对应的模板到Node，实现不同类型的Node节点

问题2的解决：

map和set底层都是红黑树，其行为都是一致的，问题在于节点数据类型的不同，所以，红黑树的底层迭代器实现都是一样的，设置为模板，因此和问题1的解决思路是一致的。

问题3的解决：


set和map的比较不一样
set的比较是直接key，而map的比较是用kv.first
不确定是map还是set，不能写死，怎么办？
可以写一个内部类的仿函数
这个仿函数，对于set返回的是其key值
对于map返回的是其kv.first值
仿函数是一个强大的功能，你想怎么实现就怎么实现

模板写成一样的，功能是一样的，但是不同的对象类具体实现不同的功能

具体解决请看以下的泛型编程过程：

二、泛型编程

1、仿函数的泛型编程


set和map的key值不一样
如何使用同一份红黑树实现不同的比较逻辑？
当对红黑树实例化时，多传一个参数，即仿函数
在红黑树底层使用一个模板仿函数
在各自的map和set写好各自的类，用于模板仿函数的实例化
这样，虽然在底层，仿函数的行为都是一致的
但是，因为模板参数不同，其返回值也就不同

set的仿函数：

	struct  SetKeyOfT
	{
		const K& operator()(const K& key)
		{
			return key;
		}

	};

map的仿函数：

		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}

		 };

红黑树部分的仿函数

		KeyOfT kot;
        kot(data)


2、迭代器的泛型编程

set和map有各自的数据类型
但是器迭代器的形式是一样的
如何做到？
迭代器实现，实在红黑树部分实现的
将之设置为模板
传set，就是se对应的迭代器
传map，就是map对应的迭代器

set的迭代器：

	typedef typename BRTree<const K,  K, SetKeyOfT>::Iterator iterator;
	iterator begin()
	{
		return _t.Begin();
	}

	iterator end()
	{
		return _t.End();
	}

map的迭代器：

	typedef typename BRTree<K, pair< K, V>, MapKeyOfT>::Iterator iterator;
	iterator begin()
	{
		return _t.Begin();
	}

	iterator end()
	{
		return  _t.End();
	}

红黑树的迭代器：

//迭代器
//referrence :引用
template<class T, class Ptr, class Ref>//迭代器模板：数据类型、指针类型、解引用
struct __RBTreeiterator
{
	typedef BRTreeNode<T> Node;
	typedef __RBTreeiterator<T, Ptr, Ref> Self;//这个迭代器的对象
	Node* _node;
	
	__RBTreeiterator( Node* node)
		:_node(node)
	{
	}
	
	//解引用
	Ref operator*()
	{
		return _node->_data;
	}

	//->
	Ptr operator->()
	{
		return &_node->_data;
	}

	//比较
	bool operator!=(const Self& s)//比较的是两个迭代器对象,参数是另外一个迭代器对象
	{
		return  _node != s._node;
	}
	
	//++
	Self& operator++()
	{
		if (_node->_right)//如果右孩子不为空，找到右子树最小孩子
		{
			Node* leftMin = _node->_right;
			while (leftMin->_left)
			{
				leftMin = leftMin->_left;
			}
			_node = leftMin;

		}
		else//右孩子为空
		{
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent && cur == parent->_right)//当孩子作为父亲的左，这个父亲就是要访问的节点
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;

		}
		return *this;//this为这个对象指针

	}

};

一般的迭代器的功能：
解引用*
指针访问->
比较相等
++
--

3、typename：

在没有实例化的对象，访问其内嵌类型 
会出现分不清楚的问题：
因为静态成员、内部类、内部成员的访问都可以使用类域的方式去访问
没有实例化，就不知道访问哪一个 

在没有实例化模板的类对象去取器内嵌类型时，加一个typename
意义就是告诉编译器，等到实例化的时候再去找对应的内嵌类型

4、++/--重载

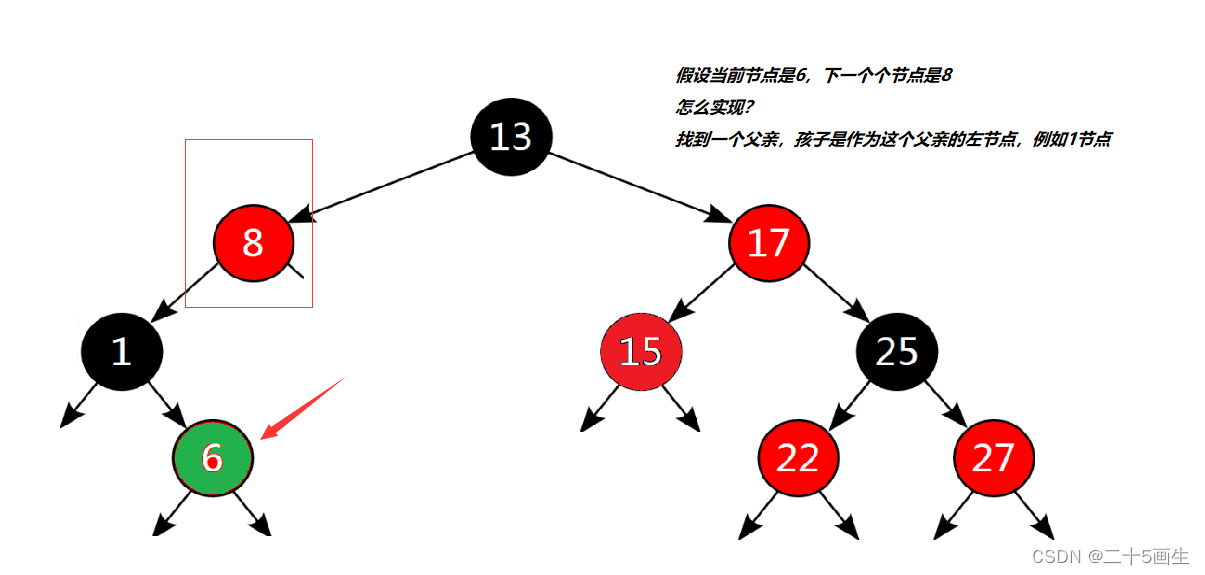
红黑树采用的是中序遍历
中序遍历，++返回的是当前节点中序遍历的下一个节点
顺序是：左，根、右
因此，需要分情况
如果当前节点有右孩子，那就是右孩子的最左节点

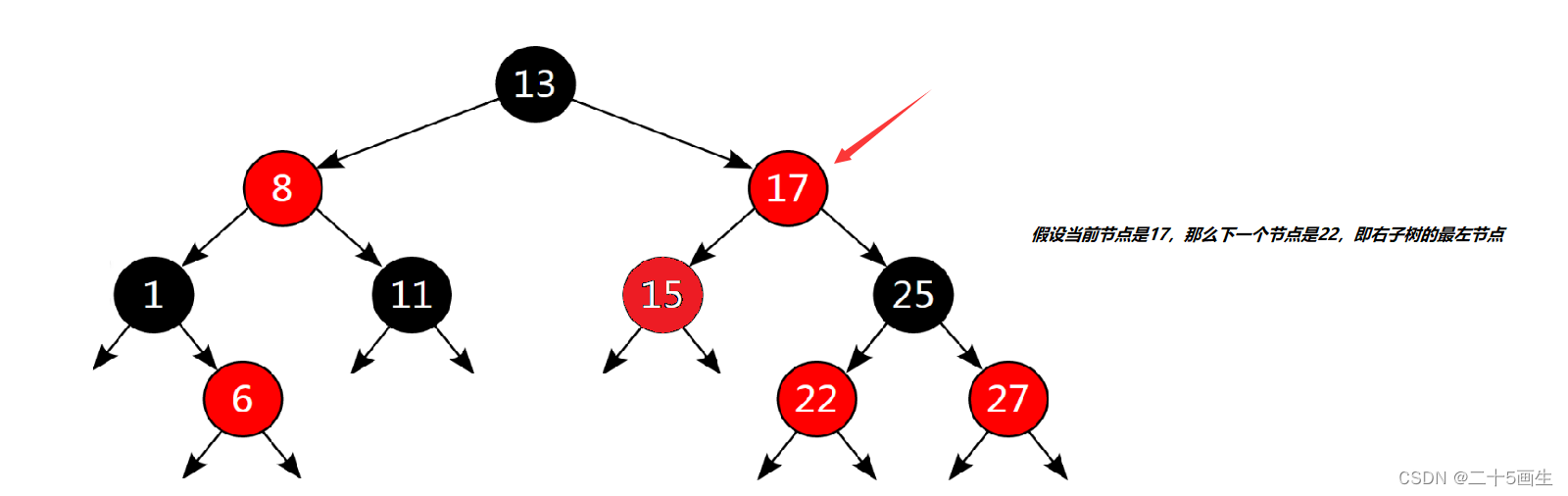
如果当前节点没有右孩子，那么说明自己这棵子树已经访问完毕
需要访问该子树的父亲，因为该子树是作为父亲的左孩子
按照中序遍历的思想，左子树访问完毕，接下来要访问的就是根

红黑树

#pragma once
#pragma once
#include<vector>
#include<iostream>
using namespace std;

enum Colour
{
	BLACK,
	RED
};

//node实例化，只给一个T
template<class T>
struct BRTreeNode
{
	BRTreeNode<T>* _parent;
	BRTreeNode<T>* _right;
	BRTreeNode<T>* _left;
	T _data;
	Colour _col;

	BRTreeNode(const T& data)
		:_parent(nullptr)
		, _right(nullptr)
		, _left(nullptr)
		, _data(data)
		, _col(RED)
	{
	}

};

//迭代器
//referrence :引用
template<class T, class Ptr, class Ref>//迭代器模板：数据类型、指针类型、解引用
struct __RBTreeiterator
{
	typedef BRTreeNode<T> Node;
	typedef __RBTreeiterator<T, Ptr, Ref> Self;//这个迭代器的对象
	Node* _node;
	
	__RBTreeiterator( Node* node)
		:_node(node)
	{
	}
	
	//解引用
	Ref operator*()
	{
		return _node->_data;
	}

	//->
	Ptr operator->()
	{
		return &_node->_data;
	}

	//比较
	bool operator!=(const Self& s)//比较的是两个迭代器对象,参数是另外一个迭代器对象
	{
		return  _node != s._node;
	}
	
	//++
	Self& operator++()
	{
		if (_node->_right)//如果右孩子不为空，找到右子树最小孩子
		{
			Node* leftMin = _node->_right;
			while (leftMin->_left)
			{
				leftMin = leftMin->_left;
			}
			_node = leftMin;

		}
		else//右孩子为空
		{
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent && cur == parent->_right)//当孩子作为父亲的左，这个父亲就是要访问的节点
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;

		}
		return *this;//this为这个对象指针

	}

};



template<class K, class T, class KeyOfT>
class BRTree
{

	typedef BRTreeNode<T> Node;
public:
	typedef  __RBTreeiterator<T, T*, T&>Iterator;
	//提供迭代器接口
	Iterator Begin()
	{
		Node* leftMin = _root;
		while (leftMin && leftMin->_left)//如果为空，直接返回
		{
			leftMin = leftMin->_left;
		}
		//返回一个迭代器
		//return leftMin;单参数的构造函数支持隐式类型转换
		return Iterator(leftMin);

	}

	Iterator End()
	{
		//遍历，要访问到最大的值为止
		//一般end位置为空
		return Iterator(nullptr);
	}


	bool Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return true;
		}

		KeyOfT kot;
		Node* cur = _root;
		Node* parent = nullptr;

		while (cur)
		{
			//现在，不知道是k还是k-v模型
			//set访问的直接是key，而map访问的.first
			//所以，对应不同的返回值，仿函数解决
			if (kot(data) < kot(cur->_data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kot(data) > kot(cur->_data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else//找到相等key
			{
				return false;
			}
		}

		cur = new Node(data);
		cur->_col = RED;
		if (kot(data) < kot(parent->_data))//插入左
		{
			parent->_left = cur;
		}
		else //插入右
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		//插入之后，要进行颜色调整
		while (parent && parent->_col == RED)//如果为空/黑色节点，直接结束
		{

			//
			Node* grandfather = parent->_parent;

			if (parent == grandfather->_left)//p为左，u为右
			{
				Node* uncle = grandfather->_right;
				//如果叔叔存在，且为红色
				if (uncle && uncle->_col == RED)
				{
					//修改颜色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;
					//向上更新
					cur = grandfather;
					parent = cur->_parent;

				}
				else//叔叔不存在/叔叔存在且为黑色
				{
					if (cur == parent->_left)
					{
						//		   g
						//	   p      u
						//  c
						//
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						//		   g
						//	   p      u
						//      c
						//
						RotateL(parent);
						//		   g
						//	   c      u
						//  p
						//
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}

			}
			else//p为右，u为左
			{
				Node* uncle = grandfather->_left;
				//如果叔叔存在，且为红色
				if (uncle && uncle->_col == RED)
				{
					//修改颜色
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;
					//向上更新
					cur = grandfather;
					parent = cur->_parent;

				}
				else//叔叔不存在/叔叔存在且为黑色
				{
					if (cur == parent->_right)
					{
						//		   g
						//	   u      p
						//					c
						//
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						//		   g
						//	   u      p
						//          c
						//
						RotateR(parent);
						//		   g
						//	   u      c
						//  				p
						//
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;

		return true;
	}

	//右旋
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)//subLR可能为空
		{
			subLR->_parent = parent;
		}

		subL->_right = parent;
		Node* ppNode = parent->_parent;
		parent->_parent = subL;

		//注意修改顺序
		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
			{
				ppNode->_left = subL;
			}
			else
			{
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}

	}

	//左旋
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}

		subR->_left = parent;

		Node* ppNode = parent->_parent;
		parent->_parent = subR;

		if (parent == _root)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
			{
				ppNode->_left = subR;
			}
			else
			{
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}

	}

	//检查平衡
	bool isBalance()
	{
		if (_root->_col == RED)
		{
			return false;
		}

		//找到任意一条路黑色节点个数
		Node* cur = _root;
		int refNum = 0;
		while (cur)
		{
			if (cur->_col == BLACK)
			{
				refNum++;
			}
			cur = cur->_left;
		}
		return Check(_root, 0, refNum);
		return 1;
	}


	void Inoder()
	{
		_Inoder(_root);
		cout << endl;
	}

private:

	bool Check(Node* root, int blackNum, const int refNum)
	{
		//到路径结束位置检查黑色节点
		if (root == nullptr)
		{
			if (blackNum != refNum)
			{
				cout << "黑色节点不相等" << endl;
				return false;
			}
			// << blackNum << endl;
			return true;
		}

		//检查红色节点
		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << root->_kv.first << "连续红节点" << endl;
			return false;
		}

		if (root->_col == BLACK)
		{
			blackNum++;
		}

		return Check(root->_left, blackNum, refNum)
			&& Check(root->_right, blackNum, refNum);
	}


	void _Inoder(const Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		_Inoder(root->_left);
		cout << root->_kv.first << ":" << _root->_kv.second << endl;
		_Inoder(root->_right);
	}

private:
	Node* _root = nullptr;

};

map

#pragma once
#include"BRTree.h"

//对map的封装

namespace myNameSpace
{

	template<class K, class V>
	class map
	{

		struct MapKeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}

		 };

	public:
		//插入
		bool insert(const  pair <K, V>& kv)
		{
			return _t.Insert(kv);
		}

		//封装红黑树的迭代器
		typedef typename BRTree<K, pair< K, V>, MapKeyOfT>::Iterator iterator;
		iterator begin()
		{
			return _t.Begin();
		}

		iterator end()
		{
			return  _t.End();
		}

		BRTree< K, pair <K, V>, MapKeyOfT> _t;
		
	};


	void test_map()
	{
		/*map<int, int> m;
		m.insert({1,1});
		m.insert({2,2});
		m.insert({3,1});
		m.insert({7,1});


		map<int,int>::iterator it = m.begin();
		while (it != m.end())
		{
			cout << it->first << ":" << it->second << endl;
			++it;
		}
		cout << endl;*/
		map<string, int> m1;
		m1.insert({ "hello",1});
		m1.insert({ "world",2});
		m1.insert({ "find",1});
		m1.insert({ "peace",1});

		map<string, int>::iterator it1 = m1.begin();
		while (it1 != m1.end())
		{
			cout << it1->first << ":" << it1->second << endl;
			++it1;
		}
		cout << endl;

	}




}

set

#pragma once
#include"BRTree.h"

namespace myNameSpace {

	template<class K>
	class set 
	{

		struct  SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}

		};

	public:
		bool insert(const K& key)
		{
			return _t.Insert(key);
		}

		
		//对于红黑树的迭代器,需要实例化红黑树的迭代器
		//所以需要在红黑树的基础上封装迭代器
		typedef typename BRTree<const K,  K, SetKeyOfT>::Iterator iterator;
		iterator begin()
		{
			return _t.Begin();
		}

		iterator end()
		{
			return _t.End();
		}

	private:
		BRTree<const K,K, SetKeyOfT> _t;
	};
	
	void test_set()
	{
		set<int> s;
		s.insert(1);
		s.insert(2);
		s.insert(4);
		s.insert(7);
		s.insert(8);
		s.insert(9);
		
		set<int>::iterator it = s.begin();
		while (it != s.end())
		{

			cout << *it << " ";
			++it;
		}
		cout << endl;

	}




}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1679345.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【STM32-MX_GPIO_Init分析】

【STM32-MX_GPIO_Init分析】

MX_GPIO_Init分析源码如下&#xff1a; __HAL_RCC_GPIOE_CLK_ENABLE源码如下&#xff1a; #define RCC ((RCC_TypeDef *) RCC_BASE) #define RCC_BASE (AHB1PERIPH_BASE 0x3800UL) #define AHB1PERIPH_BASE (PERIPH_BASE 0x00020000U…
阅读更多...
2024-简单点-ultralytics库解析-data模块

2024-简单点-ultralytics库解析-data模块

data模块 overview布局\_\_init__.pyfrom .base import BaseDataset\_\_all__ annotator.pyaugment.pyclass BaseTransformclass Composeclass BaseMixTransformclass Mosaic静态方法更新label class MixUpRandomPerspectiveclass RandomHSVclass RandomFlipclass LetterBoxcla…
阅读更多...
搭载全新升级viaim AI，讯飞会议耳机Pro 2首销价1399元起

搭载全新升级viaim AI，讯飞会议耳机Pro 2首销价1399元起

2024年5月15日&#xff0c;人工智能硬件公司未来智能发布了讯飞会议耳机Pro 2、iFLYBUDS 2以及Kit 2三款旗舰新品&#xff0c;为用户带来全新升级的viaim AI&#xff0c;也为AIGC智能耳机树立了新标杆。 在发布会上&#xff0c;未来智能CEO马啸表示&#xff1a;在AIGC领域&…
阅读更多...
20232803 2023-2024-2 《网络攻防实践》实践九报告

20232803 2023-2024-2 《网络攻防实践》实践九报告

目录 1.实践内容2.实践过程2.1 手工修改可执行文件&#xff0c;改变程序执行流程&#xff0c;直接跳转到getShell函数2.2 利用foo函数的Bof漏洞&#xff0c;构造一个攻击输入字符串&#xff0c;覆盖返回地址&#xff0c;触发getShell函数2.3 注入一个自己制作的shellcode并运行…
阅读更多...
数论专题练习

数论专题练习

质数专题 我的思路就是一个素数筛&#xff0c;然后双指针 class Solution { public:int maximumPrimeDifference(vector<int>& nums) {unordered_map<int, int> mp;for (int i 2; i < 100; i) {if (mp[i] 0) {for (int j 2 * i; j < 100; j i) {mp[…
阅读更多...
将PDF转换成电子杂志，轻松打造畅销内容！

将PDF转换成电子杂志，轻松打造畅销内容！

在数字化时代&#xff0c;将PDF转换成电子杂志是一种非常受欢迎的内容创作方式。这种方式不仅可以提高内容的传播效果&#xff0c;还可以为创作者带来更多的收益。那么&#xff0c;如何轻松地将PDF转换成电子杂志&#xff0c;打造畅销内容呢&#xff1f; 市面上有许多可以将PDF…
阅读更多...
vivo X100s发布，搭载最新天玑9300+平台

vivo X100s发布，搭载最新天玑9300+平台

在沉寂了半年后&#xff0c;vivo终于发布了新的旗舰产品。相较于前代的X100&#xff0c;X100s作为小迭代也有不少让人眼前一亮的地方&#xff0c;下面就让我们一同来了解下吧。 外观方面&#xff0c;虽然vivo X100s相较于X100没有大改&#xff0c;但却十分具有质感。以“青云”…
阅读更多...
Android 逆向

Android 逆向

一、apk 查壳工具 ApkScan-PKID 相关APK文件可以在 豌豆荚 官网下载 ApkScan-PKID查壳工具 下载 - 简书 (jianshu.com) 二、脱壳工具&#xff1a;frida 1、Android端配置 frida-server&#xff1a; 该步骤需要使用到 adb&#xff0c;操作Android文件 Releases frida/frid…
阅读更多...
机器学习中10种损失函数大梳理！建议收藏，你一定用得到

机器学习中10种损失函数大梳理！建议收藏，你一定用得到

今儿想和大家聊聊关于损失函数方面的问题。 损失函数&#xff08;Loss Function&#xff09;是在机器学习和深度学习中用来衡量模型预测值与真实标签之间差异的函数。不同的任务和模型可能需要不同的损失函数。 今天就聊聊下面常见的损失函数&#xff0c;关于原理、使用场景&…
阅读更多...
高效调度新篇章：详解DolphinScheduler 3.2.0生产级集群搭建

高效调度新篇章：详解DolphinScheduler 3.2.0生产级集群搭建

转载自tuoluzhe8521 导读&#xff1a;通过简化复杂的任务依赖关系&#xff0c; DolphinScheduler为数据工程师提供了强大的工作流程管理和调度能力。在3.2.0版本中&#xff0c;DolphinScheduler带来了一系列新功能和改进&#xff0c;使其在生产环境中的稳定性和可用性得到了显著…
阅读更多...
Apache2.4和PHP8的量子纠缠

Apache2.4和PHP8的量子纠缠

Apache不建议你用&#xff0c;PHP建议使用
阅读更多...
更新Windows 11 后遇到的一些问题（更新中...）

更新Windows 11 后遇到的一些问题（更新中...）

目录 插入U盘后读取不到 在磁盘中新建文件夹需要管理员权限 导致不能安装一些软件 插入U盘后读取不到 解决方法&#xff1a;点击我的电脑或者是此电脑、选择管理、找到设备管理器、选择通用串行总线控制器、右键、选择启动。 第一步&#xff1a;点击我的电脑或者是此电脑、选…
阅读更多...
Java类和对象（二）—— 封装，static 关键字与代码块

Java类和对象（二）—— 封装，static 关键字与代码块

前言 在面向对象的编程语言中&#xff0c;有三大特性&#xff1a;封装、继承和多态~~ 今天我们就来学习封装的知识 封装 什么是封装 在现实生活中&#xff0c;我们经常使用手机来进行沟通与交流&#xff0c;实际上我们拿到的手机是被封装好的&#xff0c;精美的屏幕&a…
阅读更多...
MYSQL和JAVA中将中文汉字按照拼音首字母排序

MYSQL和JAVA中将中文汉字按照拼音首字母排序

一、MYSQL将中文汉字按照拼音首字母排序 数据库使用的字符编码是utf8_general_ci&#xff0c;如下 ORDER BY CONVERT(表名.字段名 USING gbk) COLLATE gbk_chinese_ci ASC;若是表查询&#xff0c;CONVERT中可以不添加表名。 查询结果如下&#xff1a; 二、JAVA中将中文汉字…
阅读更多...
自定义 Gradle 插件进行统一的静态代码分析

自定义 Gradle 插件进行统一的静态代码分析

静态代码分析是一项了不起的技术, 它能让代码库更易于维护. 但是, 如果你在不同的版本库中拥有多个服务(可能由不同的团队开发), 如何才能让每个人都遵循既定的代码风格呢? 一个好办法是将所有规则封装在一个插件中, 该插件会在每个项目构建时自动执行所需的验证. 因此, 在本…
阅读更多...
【2024系统架构设计】回顾历史，查缺补漏篇 ③

【2024系统架构设计】回顾历史，查缺补漏篇 ③

前言 hello，大家好： 💡💡💡 我们一起来备考软考高级系统架构设计师吧，本专栏提供综合知识、案例科目、论文(论点和部分示例范文)等内容，包括知识点总结和记忆小妙招哦。 🚀🚀🚀 可以减少资料查找和收集的时间，提高效率，我们一起集中精力学习干货吧！ 💡…
阅读更多...
Milvus的存储/计算分离

Milvus的存储/计算分离

前言 根据数据面与控制面相隔离的原则&#xff0c;从可扩展性和灾难恢复来看&#xff0c;Milvus由4个相互独立的层组成 访问层 由一系列无状态的代理组成&#xff0c;访问层是系统和用户之间的第一层&#xff0c;它主要是验证客户端请求和规整返回的结果 代理是无状态的&am…
阅读更多...
GPU学习记一下线程分组相关

GPU学习记一下线程分组相关

在compute的时候&#xff0c;是要dispatch一个数量的代表分了多少块任务集&#xff0c;dispatch的块内部也是有一个数量的&#xff0c;那么这些值怎么取的呢 内部&#xff0c;N卡32 外面dispatch的数量就是all/32 然后细说这个值 这有一个叫core的东西&#xff0c;就是相当于th…
阅读更多...
【opencv】答题卡判分实验

【opencv】答题卡判分实验

实验环境&#xff1a; anaconda、jupyter notebook 实验用的包&#xff1a;numpy、matplotlib、opencv 实验的目的还是以熟悉图像的透视变换、轮廓特征提取为主要目的 关于如何判断答题卡被选项&#xff1a;通过几个覆盖备选项的掩膜与原二值图像想与&#xff0c;最终整个图像…
阅读更多...
Springboot+MybatisPlus如何实现带验证码的登录功能

Springboot+MybatisPlus如何实现带验证码的登录功能

实现带验证码的登录功能由两部分组成&#xff1a;&#xff1a;1、验证码的获取 2、登录&#xff08;进行用户名、密码和验证码的判断&#xff09; 获取验证码 获取验证码需要使用HuTool中的CaptchaUtil.createLineCaptcha()来定义验证码的长度、宽度、验证码位数以及干扰线…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023